
Question Number 102701 by 175mohamed last updated on 10/Jul/20

$${Evaluate}: \\ $$$$\int\frac{\mathrm{sin}\:{x}}{{x}}{dx} \\ $$
Commented by M±th+et+s last updated on 10/Jul/20
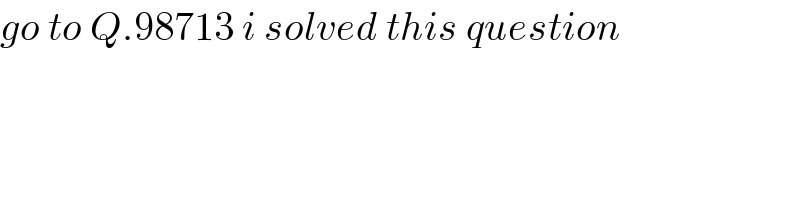
$${go}\:{to}\:{Q}.\mathrm{98713}\:{i}\:{solved}\:{this}\:{question} \\ $$
Answered by PRITHWISH SEN 2 last updated on 10/Jul/20
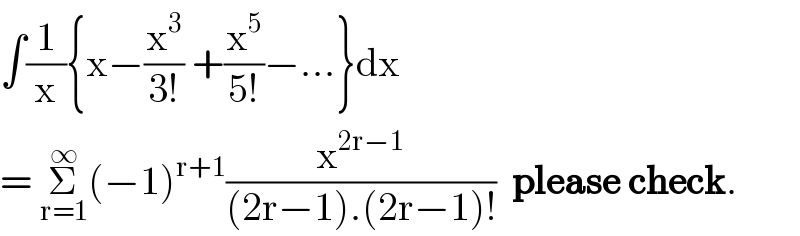
$$\int\frac{\mathrm{1}}{\mathrm{x}}\left\{\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{5}!}−...\right\}\mathrm{dx} \\ $$$$=\:\underset{\mathrm{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{r}+\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2r}−\mathrm{1}} }{\left(\mathrm{2r}−\mathrm{1}\right).\left(\mathrm{2r}−\mathrm{1}\right)!}\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Answered by mathmax by abdo last updated on 10/Jul/20
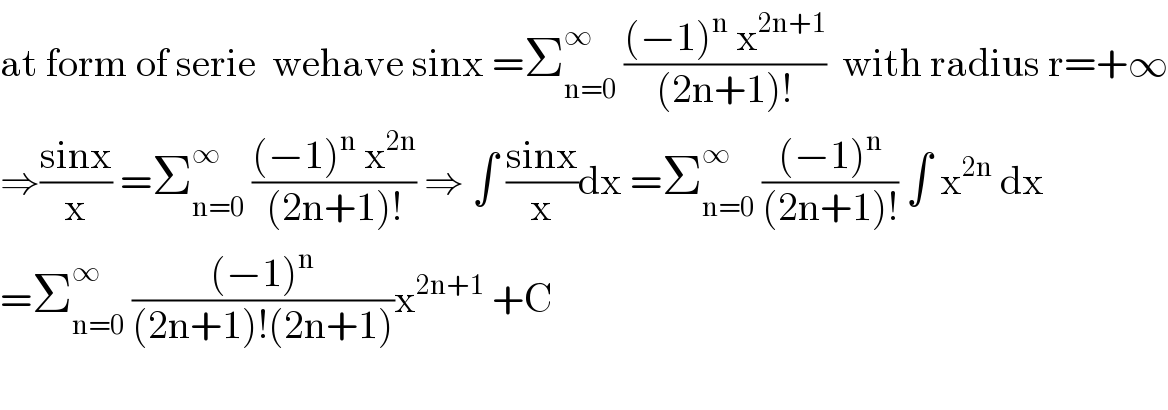
$$\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie}\:\:\mathrm{wehave}\:\mathrm{sinx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\:\mathrm{with}\:\mathrm{radius}\:\mathrm{r}=+\infty \\ $$$$\Rightarrow\frac{\mathrm{sinx}}{\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\Rightarrow\:\int\:\frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\int\:\mathrm{x}^{\mathrm{2n}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!\left(\mathrm{2n}+\mathrm{1}\right)}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \:+\mathrm{C} \\ $$$$ \\ $$
