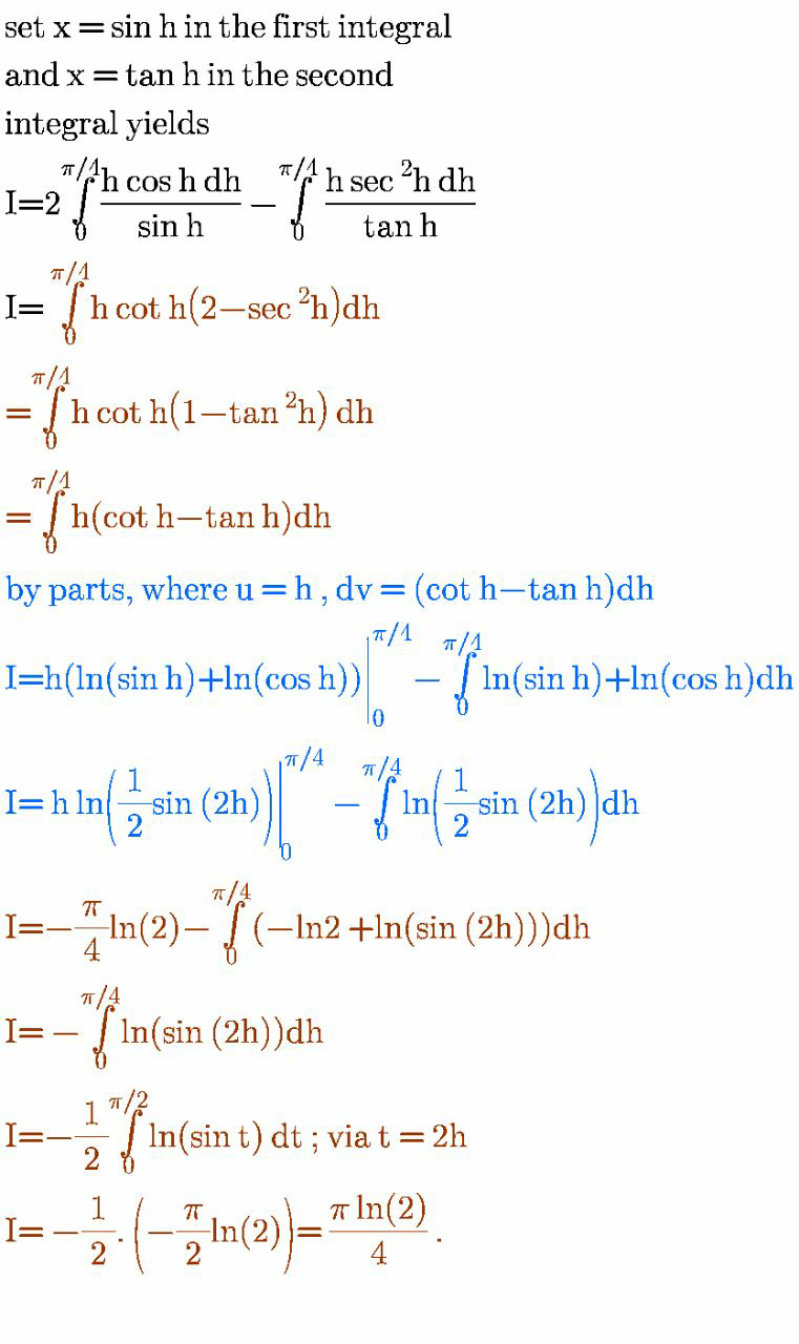Question Number 102905 by bemath last updated on 11/Jul/20

$${I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} {\int}}\:\frac{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}{{x}}\:{dx}\:−\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{x}}{dx} \\ $$
Answered by bramlex last updated on 11/Jul/20