
Question Number 102804 by bramlex last updated on 11/Jul/20

$$\mathrm{The}\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{two}\:\mathrm{points}\:\mathrm{A} \\ $$ $$\&\:\mathrm{B}\:\mathrm{are}\:\left(\mathrm{0},\mathrm{8}\right)\:\mathrm{and}\:\left(\mathrm{9},\mathrm{4}\right) \\ $$ $$\mathrm{respectively}.\:\mathrm{The}\:\mathrm{point}\:\mathrm{P}\:\mathrm{with} \\ $$ $$\mathrm{coordinate}\:\left(\mathrm{p},\mathrm{0}\right)\:\mathrm{lies}\:\mathrm{on}\:\mathrm{the} \\ $$ $$\mathrm{x}−\mathrm{axis}\:\mathrm{where}\:\mathrm{0}<\mathrm{p}<\mathrm{9}.\:\mathrm{Let}\:\mathrm{s} \\ $$ $$\mathrm{denotes}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of} \\ $$ $$\mathrm{two}\:\mathrm{segments}\:\mathrm{PA}\:\mathrm{and}\:\mathrm{PB}\:.\:\mathrm{by} \\ $$ $$\mathrm{expressing}\:\mathrm{s}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{p} \\ $$ $$\mathrm{otherwise},\:\mathrm{show}\:\mathrm{that}\:\frac{\mathrm{ds}}{\mathrm{dp}}\:= \\ $$ $$\frac{\mathrm{p}}{\sqrt{\mathrm{64}+\mathrm{p}^{\mathrm{2}} }}\:−\:\frac{\mathrm{9}−\mathrm{p}}{\sqrt{\mathrm{16}+\left(\mathrm{9}−\mathrm{p}\right)^{\mathrm{2}} }} \\ $$
Answered by bemath last updated on 11/Jul/20
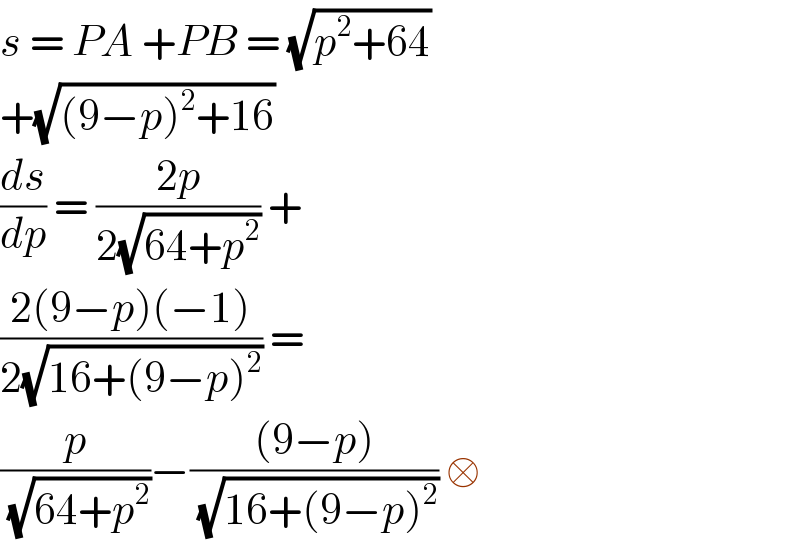
$${s}\:=\:{PA}\:+{PB}\:=\:\sqrt{{p}^{\mathrm{2}} +\mathrm{64}} \\ $$ $$+\sqrt{\left(\mathrm{9}−{p}\right)^{\mathrm{2}} +\mathrm{16}} \\ $$ $$\frac{{ds}}{{dp}}\:=\:\frac{\mathrm{2}{p}}{\mathrm{2}\sqrt{\mathrm{64}+{p}^{\mathrm{2}} }}\:+ \\ $$ $$\frac{\mathrm{2}\left(\mathrm{9}−{p}\right)\left(−\mathrm{1}\right)}{\mathrm{2}\sqrt{\mathrm{16}+\left(\mathrm{9}−{p}\right)^{\mathrm{2}} }}\:= \\ $$ $$\frac{{p}}{\sqrt{\mathrm{64}+{p}^{\mathrm{2}} }}−\frac{\left(\mathrm{9}−{p}\right)}{\sqrt{\mathrm{16}+\left(\mathrm{9}−{p}\right)^{\mathrm{2}} }}\:\square \\ $$
