Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 102838 by ajfour last updated on 11/Jul/20

Commented by ajfour last updated on 11/Jul/20

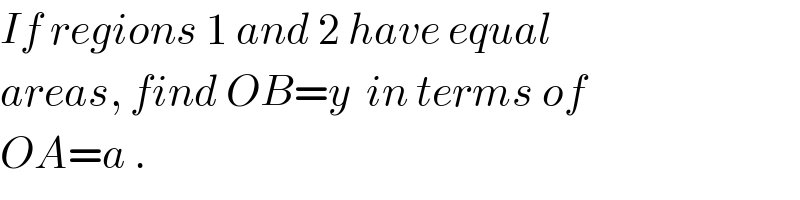
If regions 1 and 2 have equal areas, find OB=y in terms of OA=a .

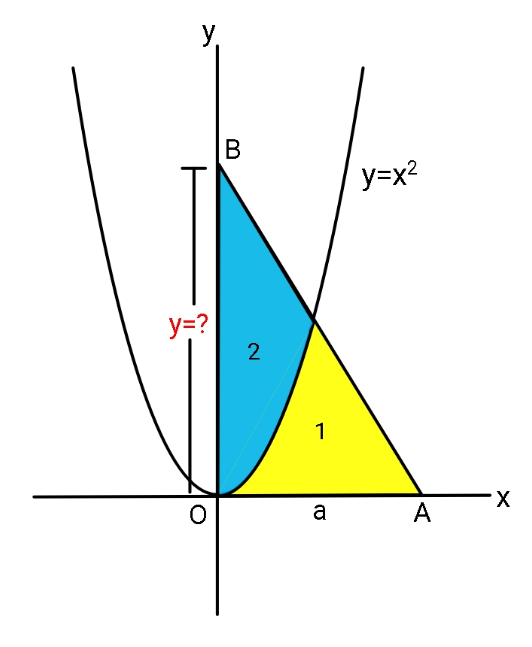
$${If}\:{regions}\:\mathrm{1}\:{and}\:\mathrm{2}\:{have}\:{equal} \\ $$$${areas},\:{find}\:{OB}={y}\:\:{in}\:{terms}\:{of} \\ $$$${OA}={a}\:. \\ $$

Commented by ajfour last updated on 11/Jul/20

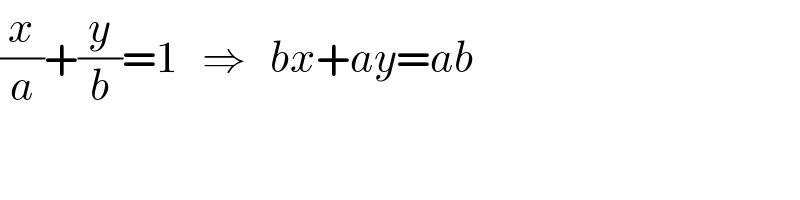
(x/a)+(y/b)=1 ⇒ bx+ay=ab

$$\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{1}\:\:\:\Rightarrow\:\:\:{bx}+{ay}={ab} \\ $$

Answered by mr W last updated on 11/Jul/20

OB=b intersection at P(p,p^2 ) (p/a)+(p^2 /b)=1 ⇒b=((ap^2 )/(a−p)) (p^3 /3)+((p^2 (a−p))/2)=(1/2)((a/(a−p)))^2 ((p^2 (a−p))/2) ⇒2p^2 −8ap+3a^2 =0 ⇒p=(((4−(√(10)))a)/2) ⇒b=((5(√(10))−14)/6)a^2 ≈0.302a^2

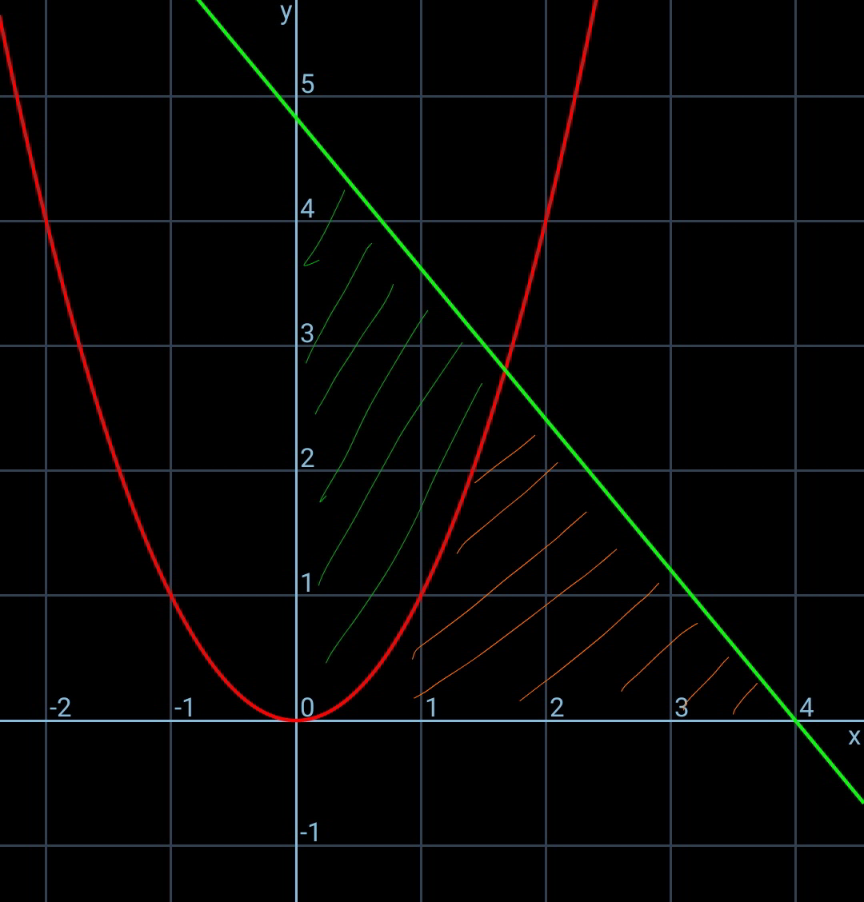
$${OB}={b} \\ $$$${intersection}\:{at}\:{P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$$\frac{{p}}{{a}}+\frac{{p}^{\mathrm{2}} }{{b}}=\mathrm{1} \\ $$$$\Rightarrow{b}=\frac{{ap}^{\mathrm{2}} }{{a}−{p}} \\ $$$$\frac{{p}^{\mathrm{3}} }{\mathrm{3}}+\frac{{p}^{\mathrm{2}} \left({a}−{p}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}}{{a}−{p}}\right)^{\mathrm{2}} \frac{{p}^{\mathrm{2}} \left({a}−{p}\right)}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{p}^{\mathrm{2}} −\mathrm{8}{ap}+\mathrm{3}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{p}=\frac{\left(\mathrm{4}−\sqrt{\mathrm{10}}\right){a}}{\mathrm{2}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{5}\sqrt{\mathrm{10}}−\mathrm{14}}{\mathrm{6}}{a}^{\mathrm{2}} \approx\mathrm{0}.\mathrm{302}{a}^{\mathrm{2}} \\ $$

Commented by mr W last updated on 11/Jul/20

Commented by ajfour last updated on 11/Jul/20

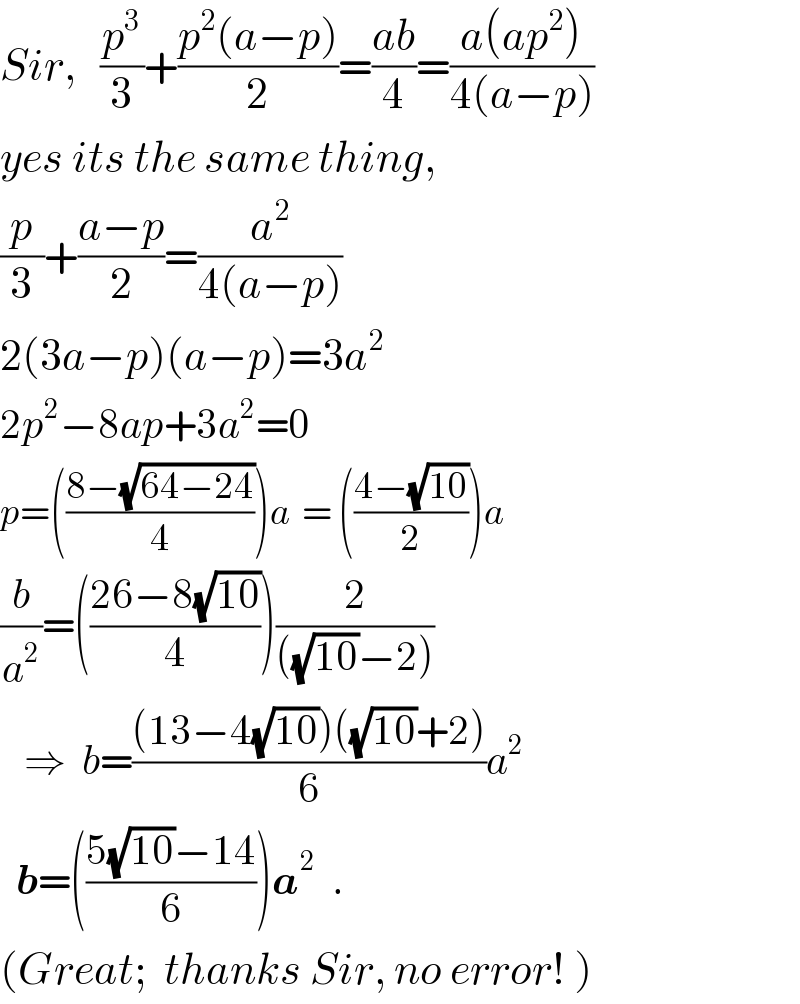
Sir, (p^3 /3)+((p^2 (a−p))/2)=((ab)/4)=((a(ap^2 ))/(4(a−p))) yes its the same thing, (p/3)+((a−p)/2)=(a^2 /(4(a−p))) 2(3a−p)(a−p)=3a^2 2p^2 −8ap+3a^2 =0 p=(((8−(√(64−24)))/4))a = (((4−(√(10)))/2))a (b/a^2 )=(((26−8(√(10)))/4))(2/(((√(10))−2))) ⇒ b=(((13−4(√(10)))((√(10))+2))/6)a^2 b=(((5(√(10))−14)/6))a^2 . (Great; thanks Sir, no error! )

$${Sir},\:\:\:\frac{{p}^{\mathrm{3}} }{\mathrm{3}}+\frac{{p}^{\mathrm{2}} \left({a}−{p}\right)}{\mathrm{2}}=\frac{{ab}}{\mathrm{4}}=\frac{{a}\left({ap}^{\mathrm{2}} \right)}{\mathrm{4}\left({a}−{p}\right)} \\ $$$${yes}\:{its}\:{the}\:{same}\:{thing},\: \\ $$$$\frac{{p}}{\mathrm{3}}+\frac{{a}−{p}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}\left({a}−{p}\right)} \\ $$$$\mathrm{2}\left(\mathrm{3}{a}−{p}\right)\left({a}−{p}\right)=\mathrm{3}{a}^{\mathrm{2}} \\ $$$$\mathrm{2}{p}^{\mathrm{2}} −\mathrm{8}{ap}+\mathrm{3}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}=\left(\frac{\mathrm{8}−\sqrt{\mathrm{64}−\mathrm{24}}}{\mathrm{4}}\right){a}\:\:=\:\left(\frac{\mathrm{4}−\sqrt{\mathrm{10}}}{\mathrm{2}}\right){a} \\ $$$$\frac{{b}}{{a}^{\mathrm{2}} }=\left(\frac{\mathrm{26}−\mathrm{8}\sqrt{\mathrm{10}}}{\mathrm{4}}\right)\frac{\mathrm{2}}{\left(\sqrt{\mathrm{10}}−\mathrm{2}\right)} \\ $$$$\:\:\:\Rightarrow\:\:{b}=\frac{\left(\mathrm{13}−\mathrm{4}\sqrt{\mathrm{10}}\right)\left(\sqrt{\mathrm{10}}+\mathrm{2}\right)}{\mathrm{6}}{a}^{\mathrm{2}} \\ $$$$\:\:\boldsymbol{{b}}=\left(\frac{\mathrm{5}\sqrt{\mathrm{10}}−\mathrm{14}}{\mathrm{6}}\right)\boldsymbol{{a}}^{\mathrm{2}} \:\:. \\ $$$$\left({Great};\:\:{thanks}\:{Sir},\:{no}\:{error}!\:\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com