Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 10294 by Tawakalitu ayo mi last updated on 02/Feb/17

A student needs at least three notebooks and three pencils. Notebooks cost #60 and pencil #36 and the student has #360 to spend. The student decides to spend as much as possible of his #360. (a) How many ways can he spend his money (b) Does any of the ways give him change ??? if so, how much ?

$$\mathrm{A}\:\mathrm{student}\:\mathrm{needs}\:\mathrm{at}\:\mathrm{least}\:\mathrm{three}\:\mathrm{notebooks}\:\mathrm{and} \\ $$$$\mathrm{three}\:\mathrm{pencils}.\:\mathrm{Notebooks}\:\mathrm{cost}\:#\mathrm{60}\:\mathrm{and}\:\mathrm{pencil} \\ $$$$#\mathrm{36}\:\mathrm{and}\:\mathrm{the}\:\mathrm{student}\:\mathrm{has}\:#\mathrm{360}\:\mathrm{to}\:\mathrm{spend}.\:\mathrm{The} \\ $$$$\mathrm{student}\:\mathrm{decides}\:\mathrm{to}\:\mathrm{spend}\:\mathrm{as}\:\mathrm{much}\:\mathrm{as}\:\mathrm{possible} \\ $$$$\mathrm{of}\:\mathrm{his}\:#\mathrm{360}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{he}\:\mathrm{spend}\:\mathrm{his}\:\mathrm{money} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Does}\:\mathrm{any}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ways}\:\mathrm{give}\:\mathrm{him}\:\mathrm{change}\:??? \\ $$$$\mathrm{if}\:\mathrm{so},\:\mathrm{how}\:\mathrm{much}\:? \\ $$

Answered by mrW1 last updated on 02/Feb/17

for 3 notebooks and 3 pencils: 3×60+3×36=288 money left: 360−288=72 there are 2 ways to spend this money: way 1: to buy 2 additional pencils for 2×36=#72 way 2: to buy 1 additional notebook for #60. way 2 gives ihm a change of #12.

$${for}\:\mathrm{3}\:{notebooks}\:{and}\:\mathrm{3}\:{pencils}: \\ $$$$\mathrm{3}×\mathrm{60}+\mathrm{3}×\mathrm{36}=\mathrm{288} \\ $$$$ \\ $$$${money}\:{left}: \\ $$$$\mathrm{360}−\mathrm{288}=\mathrm{72} \\ $$$$ \\ $$$${there}\:{are}\:\mathrm{2}\:{ways}\:{to}\:{spend}\:{this}\:{money}: \\ $$$${way}\:\mathrm{1}:\:{to}\:{buy}\:\mathrm{2}\:{additional}\:{pencils}\:{for}\:\mathrm{2}×\mathrm{36}=#\mathrm{72} \\ $$$${way}\:\mathrm{2}:\:{to}\:{buy}\:\mathrm{1}\:{additional}\:{notebook}\:{for}\:#\mathrm{60}. \\ $$$$ \\ $$$${way}\:\mathrm{2}\:{gives}\:{ihm}\:{a}\:{change}\:{of}\:#\mathrm{12}. \\ $$

Commented by Tawakalitu ayo mi last updated on 02/Feb/17

wow, God bless you sir.

$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by sandy_suhendra last updated on 02/Feb/17

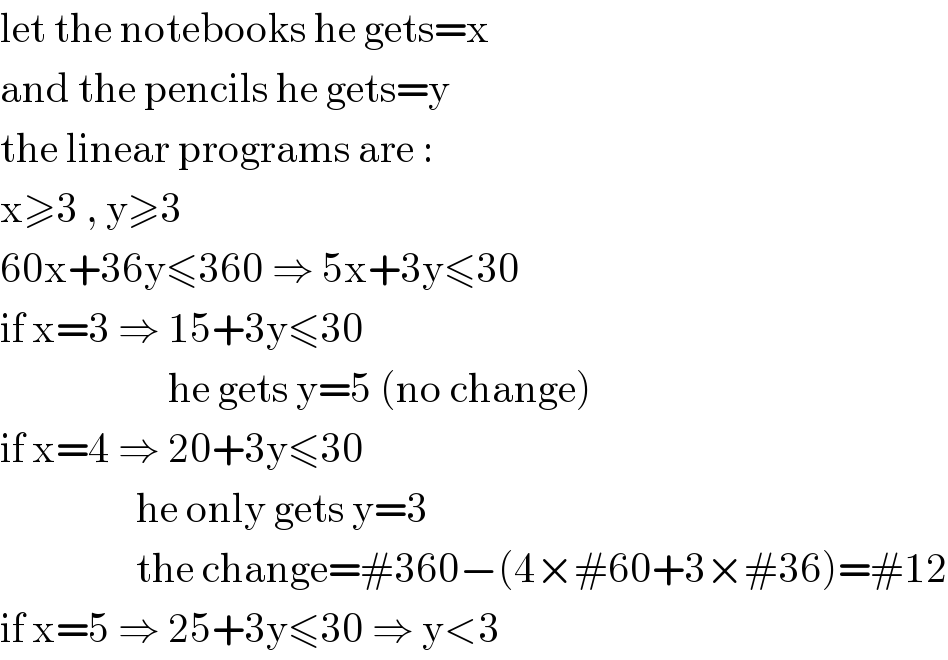
let the notebooks he gets=x and the pencils he gets=y the linear programs are : x≥3 , y≥3 60x+36y≤360 ⇒ 5x+3y≤30 if x=3 ⇒ 15+3y≤30 he gets y=5 (no change) if x=4 ⇒ 20+3y≤30 he only gets y=3 the change=#360−(4×#60+3×#36)=#12 if x=5 ⇒ 25+3y≤30 ⇒ y<3

$$\mathrm{let}\:\mathrm{the}\:\mathrm{notebooks}\:\mathrm{he}\:\mathrm{gets}=\mathrm{x} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{pencils}\:\mathrm{he}\:\mathrm{gets}=\mathrm{y} \\ $$$$\mathrm{the}\:\mathrm{linear}\:\mathrm{programs}\:\mathrm{are}\:: \\ $$$$\mathrm{x}\geqslant\mathrm{3}\:,\:\mathrm{y}\geqslant\mathrm{3} \\ $$$$\mathrm{60x}+\mathrm{36y}\leqslant\mathrm{360}\:\Rightarrow\:\mathrm{5x}+\mathrm{3y}\leqslant\mathrm{30} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{3}\:\Rightarrow\:\mathrm{15}+\mathrm{3y}\leqslant\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{he}\:\mathrm{gets}\:\mathrm{y}=\mathrm{5}\:\left(\mathrm{no}\:\mathrm{change}\right) \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{4}\:\Rightarrow\:\mathrm{20}+\mathrm{3y}\leqslant\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{he}\:\mathrm{only}\:\mathrm{gets}\:\mathrm{y}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{the}\:\mathrm{change}=#\mathrm{360}−\left(\mathrm{4}×#\mathrm{60}+\mathrm{3}×#\mathrm{36}\right)=#\mathrm{12} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{5}\:\Rightarrow\:\mathrm{25}+\mathrm{3y}\leqslant\mathrm{30}\:\Rightarrow\:\mathrm{y}<\mathrm{3} \\ $$

Commented by Tawakalitu ayo mi last updated on 02/Feb/17

wow, God bless you sir.

$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by arge last updated on 03/Feb/17

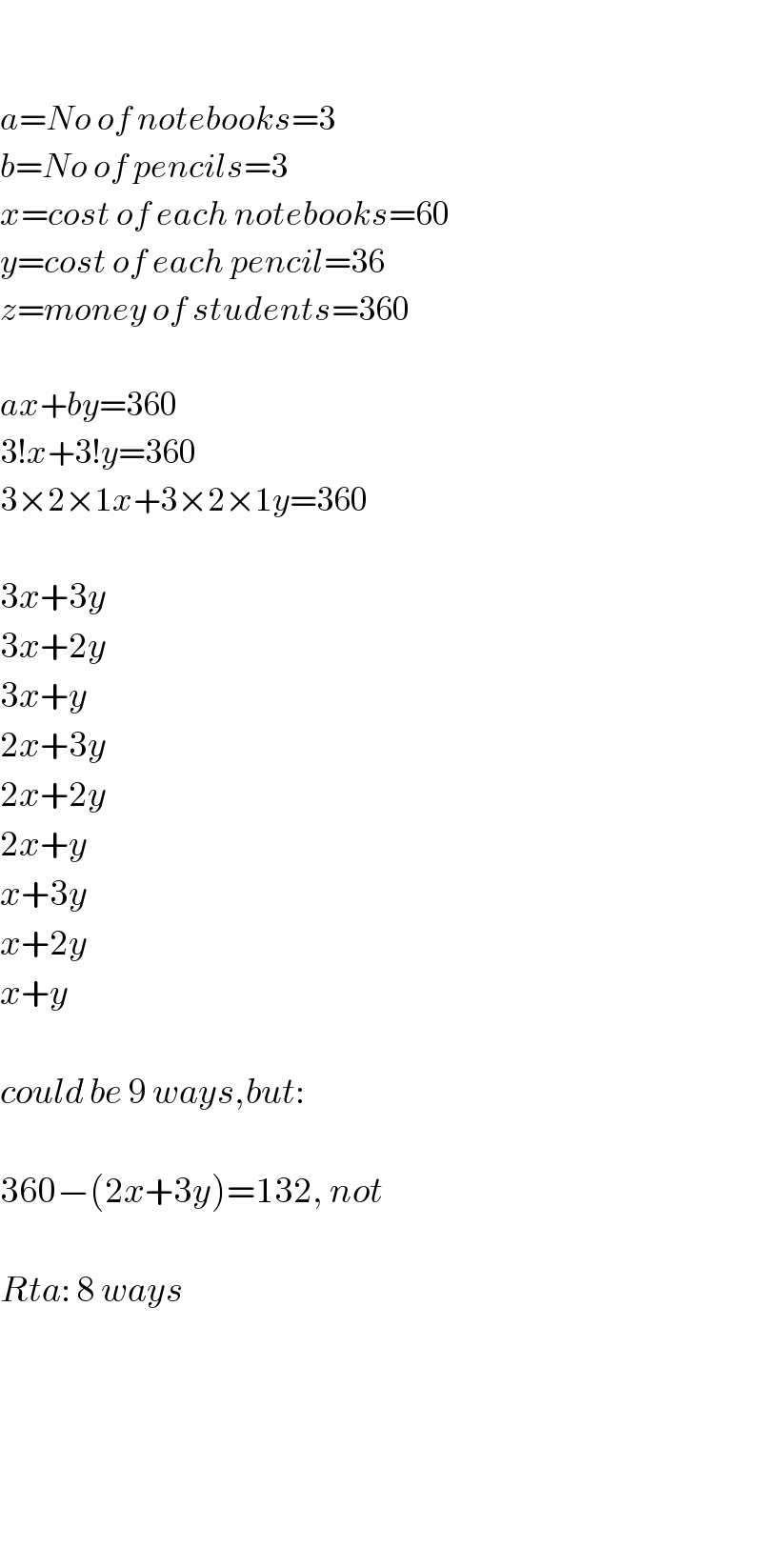
a=No of notebooks=3 b=No of pencils=3 x=cost of each notebooks=60 y=cost of each pencil=36 z=money of students=360 ax+by=360 3!x+3!y=360 3×2×1x+3×2×1y=360 3x+3y 3x+2y 3x+y 2x+3y 2x+2y 2x+y x+3y x+2y x+y could be 9 ways,but: 360−(2x+3y)=132, not Rta: 8 ways

$$ \\ $$$$ \\ $$$${a}={No}\:{of}\:{notebooks}=\mathrm{3} \\ $$$${b}={No}\:{of}\:{pencils}=\mathrm{3} \\ $$$${x}={cost}\:{of}\:{each}\:{notebooks}=\mathrm{60} \\ $$$${y}={cost}\:{of}\:{each}\:{pencil}=\mathrm{36} \\ $$$${z}={money}\:{of}\:{students}=\mathrm{360} \\ $$$$ \\ $$$${ax}+{by}=\mathrm{360} \\ $$$$\mathrm{3}!{x}+\mathrm{3}!{y}=\mathrm{360} \\ $$$$\mathrm{3}×\mathrm{2}×\mathrm{1}{x}+\mathrm{3}×\mathrm{2}×\mathrm{1}{y}=\mathrm{360} \\ $$$$ \\ $$$$\mathrm{3}{x}+\mathrm{3}{y} \\ $$$$\mathrm{3}{x}+\mathrm{2}{y} \\ $$$$\mathrm{3}{x}+{y} \\ $$$$\mathrm{2}{x}+\mathrm{3}{y} \\ $$$$\mathrm{2}{x}+\mathrm{2}{y} \\ $$$$\mathrm{2}{x}+{y} \\ $$$${x}+\mathrm{3}{y} \\ $$$${x}+\mathrm{2}{y} \\ $$$${x}+{y} \\ $$$$ \\ $$$${could}\:{be}\:\mathrm{9}\:{ways},{but}: \\ $$$$ \\ $$$$\mathrm{360}−\left(\mathrm{2}{x}+\mathrm{3}{y}\right)=\mathrm{132},\:{not} \\ $$$$ \\ $$$${Rta}:\:\mathrm{8}\:{ways} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Tawakalitu ayo mi last updated on 03/Feb/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com