Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 102980 by ajfour last updated on 12/Jul/20

Commented by ajfour last updated on 12/Jul/20

Find a/b if regions 1, 2, 3, 4, 5 have equal areas.

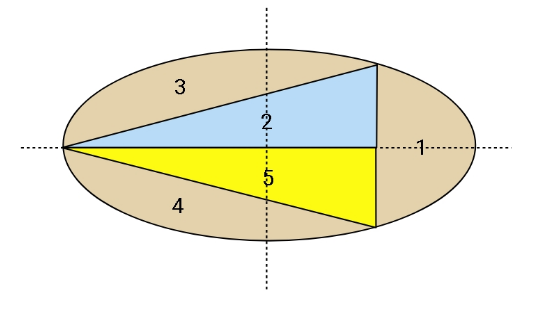
$${Find}\:\:{a}/{b}\:\:{if}\:{regions}\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5} \\ $$$${have}\:{equal}\:{areas}. \\ $$

Commented by mr W last updated on 12/Jul/20

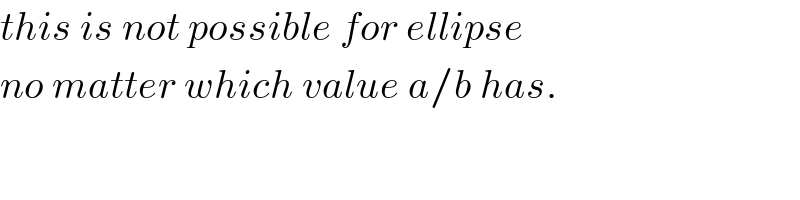
this is not possible for ellipse no matter which value a/b has.

$${this}\:{is}\:{not}\:{possible}\:{for}\:{ellipse} \\ $$$${no}\:{matter}\:{which}\:{value}\:{a}/{b}\:{has}. \\ $$

Commented by mr W last updated on 12/Jul/20

if this is true, say for a certain value of a/b, then it must be also true when we shrink the ellipse in x−direction in ratio b/a to a circle with radius r=b. that means each of the three shaded segments of the circle must have fifth of the area of the circle. but this is not possible, since area of segement =(b^2 /2)(((2π)/3)−((√3)/2))≠((πb^2 )/5)

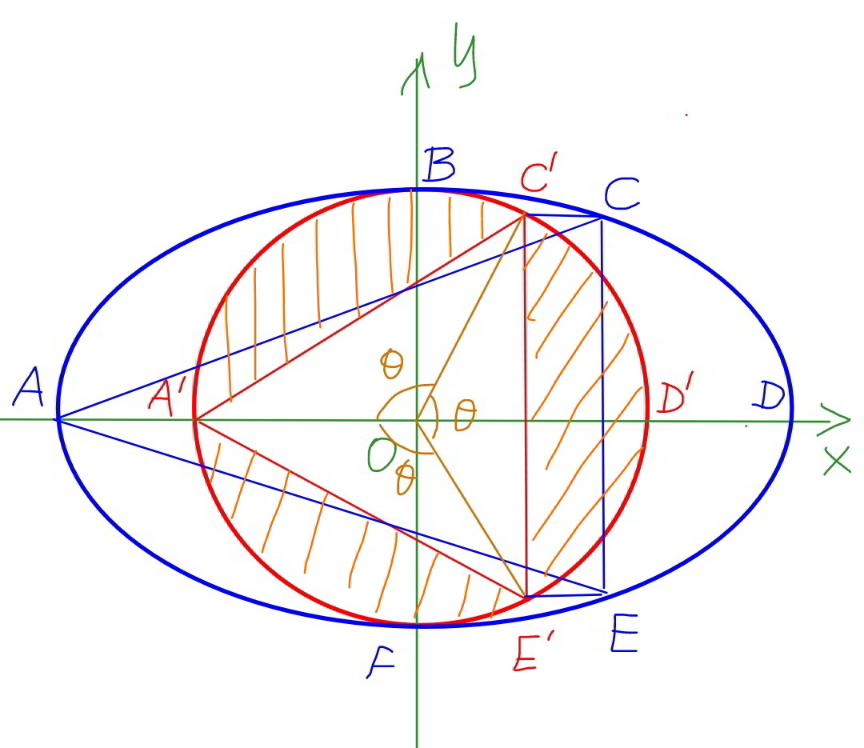
$${if}\:{this}\:{is}\:{true},\:{say}\:{for}\:{a}\:{certain} \\ $$$${value}\:{of}\:{a}/{b},\:{then}\:{it}\:{must}\:{be}\:{also}\:{true} \\ $$$${when}\:{we}\:{shrink}\:{the}\:{ellipse}\:{in} \\ $$$${x}−{direction}\:{in}\:{ratio}\:{b}/{a}\:{to}\:{a}\:{circle} \\ $$$${with}\:{radius}\:{r}={b}. \\ $$$${that}\:{means}\:{each}\:{of}\:{the}\:{three}\:{shaded} \\ $$$${segments}\:{of}\:{the}\:{circle}\:{must}\:{have}\: \\ $$$${fifth}\:{of}\:{the}\:{area}\:{of}\:{the}\:{circle}.\:{but} \\ $$$${this}\:{is}\:{not}\:{possible},\:{since} \\ $$$${area}\:{of}\:{segement}\:=\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\neq\frac{\pi{b}^{\mathrm{2}} }{\mathrm{5}} \\ $$

Commented by mr W last updated on 12/Jul/20

Commented by ajfour last updated on 12/Jul/20

′′ then it must be also true when we shrink the ellipse ′′ may not necessarily be true Sir....

$$''\:\:{then}\:{it}\:{must}\:{be}\:{also}\:{true} \\ $$$${when}\:{we}\:{shrink}\:{the}\:{ellipse}\:'' \\ $$$$\:\:\:\:\:{may}\:{not}\:{necessarily}\:{be}\:{true} \\ $$$$\:\:\:\:\:{Sir}.... \\ $$

Commented by mr W last updated on 12/Jul/20

when an ellipse is shrinked in x−direction in ratio (b/a), the area of each part is shrinked in the same ratio (b/a): A_1 →A_1 ^′ =(b/a)A_1 A_2 →A_2 ^′ =(b/a)A_2 ... therefore if A_1 =A_2 =A_3 =..., we get also A_1 ′=A_2 ′=A_3 ′=...

$${when}\:{an}\:{ellipse}\:{is}\:{shrinked}\:{in} \\ $$$${x}−{direction}\:{in}\:{ratio}\:\frac{{b}}{{a}},\:{the}\:{area}\:{of} \\ $$$${each}\:{part}\:{is}\:{shrinked}\:{in}\:{the}\:{same} \\ $$$${ratio}\:\frac{{b}}{{a}}: \\ $$$${A}_{\mathrm{1}} \:\rightarrow{A}_{\mathrm{1}} ^{'} =\frac{{b}}{{a}}{A}_{\mathrm{1}} \\ $$$${A}_{\mathrm{2}} \:\rightarrow{A}_{\mathrm{2}} ^{'} =\frac{{b}}{{a}}{A}_{\mathrm{2}} \\ $$$$... \\ $$$${therefore}\:{if}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} ={A}_{\mathrm{3}} =...,\:{we}\:{get} \\ $$$${also}\:{A}_{\mathrm{1}} '={A}_{\mathrm{2}} '={A}_{\mathrm{3}} '=... \\ $$

Answered by ajfour last updated on 12/Jul/20

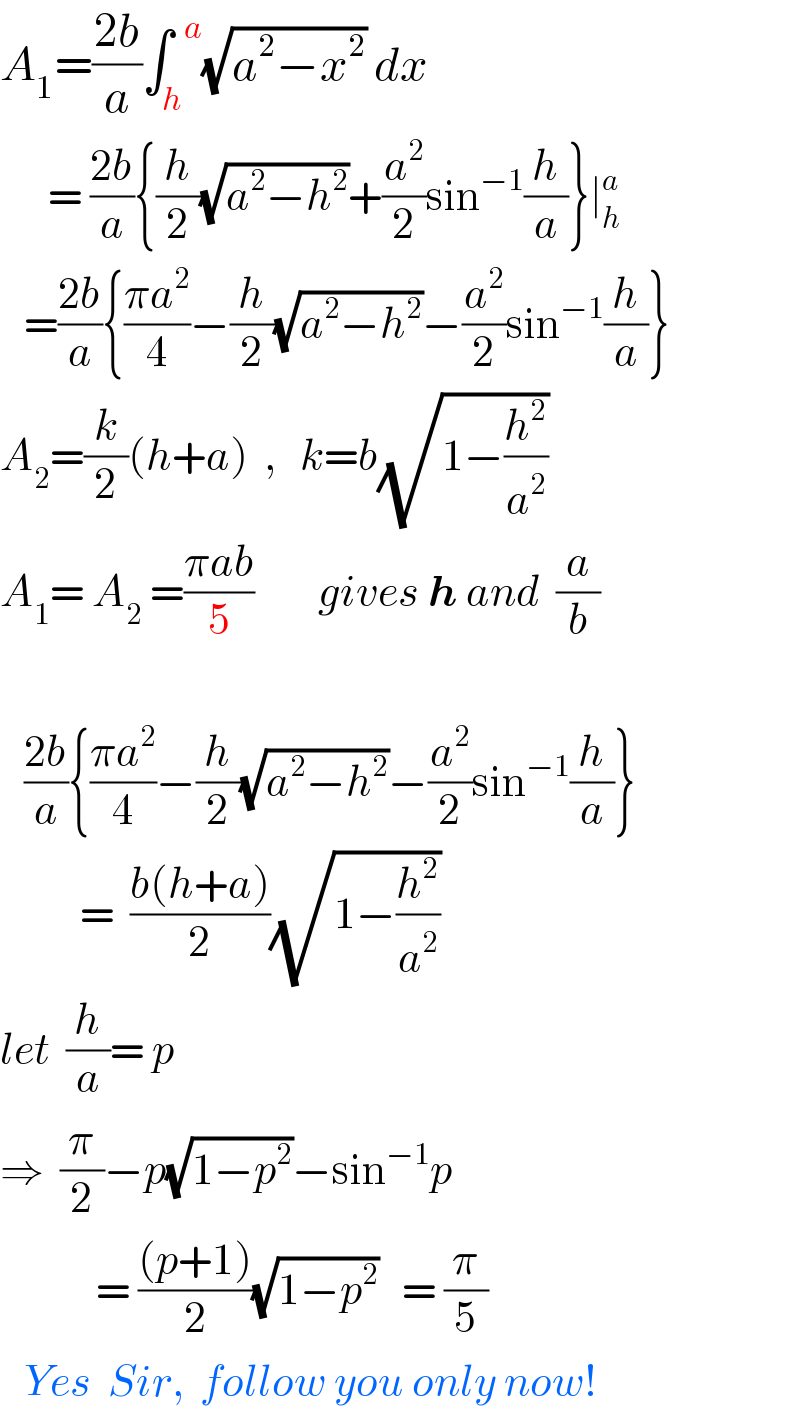
A_1 =((2b)/a)∫_h ^( a) (√(a^2 −x^2 )) dx = ((2b)/a){(h/2)(√(a^2 −h^2 ))+(a^2 /2)sin^(−1) (h/a)}∣_h ^a =((2b)/a){((πa^2 )/4)−(h/2)(√(a^2 −h^2 ))−(a^2 /2)sin^(−1) (h/a)} A_2 =(k/2)(h+a) , k=b(√(1−(h^2 /a^2 ))) A_1 = A_2 =((πab)/5) gives h and (a/b) ((2b)/a){((πa^2 )/4)−(h/2)(√(a^2 −h^2 ))−(a^2 /2)sin^(−1) (h/a)} = ((b(h+a))/2)(√(1−(h^2 /a^2 ))) let (h/a)= p ⇒ (π/2)−p(√(1−p^2 ))−sin^(−1) p = (((p+1))/2)(√(1−p^2 )) = (π/5) Yes Sir, follow you only now!

$${A}_{\mathrm{1}} =\frac{\mathrm{2}{b}}{{a}}\int_{{h}} ^{\:\:{a}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{2}{b}}{{a}}\left\{\frac{{h}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{h}}{{a}}\right\}\mid_{{h}} ^{{a}} \\ $$$$\:\:\:=\frac{\mathrm{2}{b}}{{a}}\left\{\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{h}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{h}}{{a}}\right\} \\ $$$${A}_{\mathrm{2}} =\frac{{k}}{\mathrm{2}}\left({h}+{a}\right)\:\:,\:\:\:{k}={b}\sqrt{\mathrm{1}−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$$${A}_{\mathrm{1}} =\:{A}_{\mathrm{2}} \:=\frac{\pi{ab}}{\mathrm{5}}\:\:\:\:\:\:\:\:{gives}\:\boldsymbol{{h}}\:{and}\:\:\frac{{a}}{{b}}\: \\ $$$$ \\ $$$$\:\:\:\frac{\mathrm{2}{b}}{{a}}\left\{\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{h}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{h}}{{a}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\:\frac{{b}\left({h}+{a}\right)}{\mathrm{2}}\sqrt{\mathrm{1}−\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }} \\ $$$${let}\:\:\frac{{h}}{{a}}=\:{p} \\ $$$$\Rightarrow\:\:\frac{\pi}{\mathrm{2}}−{p}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }−\mathrm{sin}^{−\mathrm{1}} {p} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\left({p}+\mathrm{1}\right)}{\mathrm{2}}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\:\:\:=\:\frac{\pi}{\mathrm{5}} \\ $$$$\:\:\:{Yes}\:\:{Sir},\:\:{follow}\:{you}\:{only}\:{now}! \\ $$

Commented by mr W last updated on 12/Jul/20

you can make A_1 =A_2 or A_1 =A_3 or A_2 =A_3 for any ellipse, but never A_1 =A_2 =A_3 .

$${you}\:{can}\:{make}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} \:{or}\:{A}_{\mathrm{1}} ={A}_{\mathrm{3}} \:{or} \\ $$$${A}_{\mathrm{2}} ={A}_{\mathrm{3}} \:{for}\:{any}\:{ellipse},\:{but}\:{never} \\ $$$${A}_{\mathrm{1}} ={A}_{\mathrm{2}} ={A}_{\mathrm{3}} . \\ $$

Commented by ajfour last updated on 12/Jul/20

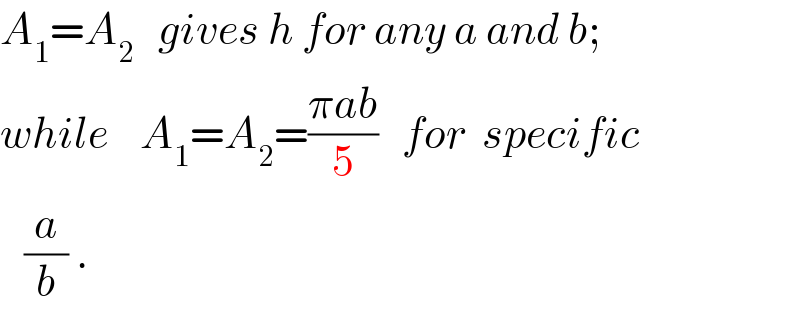
A_1 =A_2 gives h for any a and b; while A_1 =A_2 =((πab)/5) for specific (a/b) .

$${A}_{\mathrm{1}} ={A}_{\mathrm{2}} \:\:\:{gives}\:{h}\:{for}\:{any}\:{a}\:{and}\:{b}; \\ $$$${while}\:\:\:\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} =\frac{\pi{ab}}{\mathrm{5}}\:\:\:{for}\:\:{specific} \\ $$$$\:\:\:\frac{{a}}{{b}}\:. \\ $$

Commented by mr W last updated on 12/Jul/20

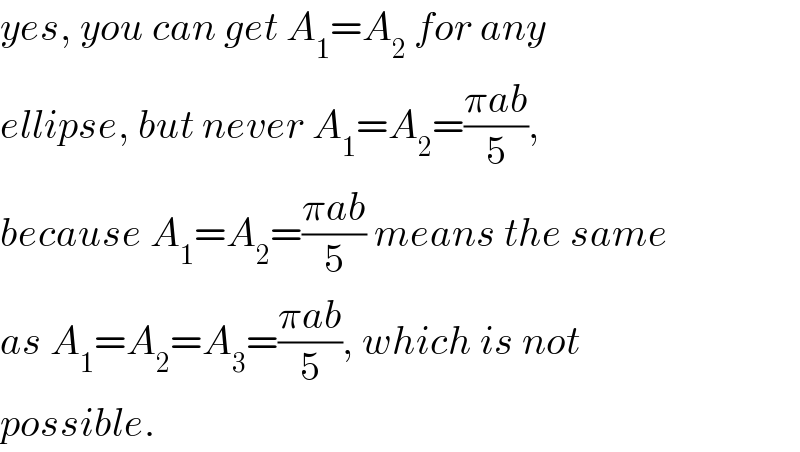
yes, you can get A_1 =A_2 for any ellipse, but never A_1 =A_2 =((πab)/5), because A_1 =A_2 =((πab)/5) means the same as A_1 =A_2 =A_3 =((πab)/5), which is not possible.

$${yes},\:{you}\:{can}\:{get}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} \:{for}\:{any} \\ $$$${ellipse},\:{but}\:{never}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} =\frac{\pi{ab}}{\mathrm{5}}, \\ $$$${because}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} =\frac{\pi{ab}}{\mathrm{5}}\:{means}\:{the}\:{same} \\ $$$${as}\:{A}_{\mathrm{1}} ={A}_{\mathrm{2}} ={A}_{\mathrm{3}} =\frac{\pi{ab}}{\mathrm{5}},\:{which}\:{is}\:{not} \\ $$$${possible}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com