Math Question and Answers


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 102985 by DGmichael last updated on 12/Jul/20

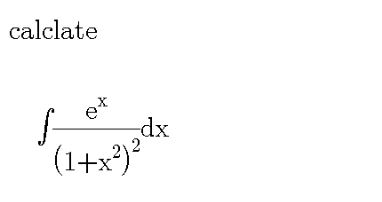
	Answered by mathmax by abdo last updated on 12/Jul/20
	$at form of serie let f(x) =∫_0 ^x (e^t /((1+t^2 )^2 ))dt if o≤x<1 we have (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^(n ) ⇒by derivation we get −(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) u^(n−1) ⇒ (1/((1+t^2 )^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) t^(2n−2) ⇒f(x) =∫_0 ^(x ) e^t (Σ_(n=1) ^(∞ ) n(−1)^(n−1 ) t^(2n−2) )dt =Σ_(n=1) ^∞ n(−1)^(n−1) ∫_0 ^(x ) t^(2n−2) e^t dt =Σ_(n=1) ^∞ n(−1)^(n−1) U_n U_n =∫_0 ^x t^(2n−2 ) e^t dt by parts u^′ =t^(2n−2) and v =e^t ⇒ U_n =[(1/(2n−1)) t^(2n−1) e^t ]_0 ^x −∫_0 ^x (1/(2n−1)) t^(2n−1) e^(t ) dt =((x^(2n−1) e^x )/(2n−1)) −(1/(2n−1)) ∫_0 ^x t^(2n−1) e^t dt and ∫_0 ^x t^(2n−1) e^t dt =[(t^(2n) /(2n)) e^t ]_0 ^x −∫_0 ^x (t^(2n) /(2n))e^t dt =((x^(2n) e^x )/(2n)) −(1/(2n)) ∫_0 ^x t^(2n) e^t dt =((x^(2n) e^x )/(2n))−(1/(2n))U_(n+1) ⇒U_n =((x^(2n−1) e^x )/(2n−1))−(1/(2n−1)){((x^(2n) e^x )/(2n))−(1/(2n)) U_(n+1) } =((x^(2n−1) e^x )/(2n−1))−((x^(2n) e^x )/((2n−1)(2n))) +(1/(2n(2n−1))) U_(n+1) ...be continued$
	$at form of serie let f (x) = \int_{0}^{x} \frac{e^{t}}{{(1 + t^{2})}^{2}} dt$ $if o ⩽ x < 1 we have \frac{1}{1 + u} = \sum_{n = 0}^{\infty} {(- 1)}^{n} u^{n} \Rightarrow by derivation we get$ $- \frac{1}{{(1 + u)}^{2}} = \sum_{n = 1}^{\infty} n {(- 1)}^{n} u^{n - 1} \Rightarrow \frac{1}{{(1 + u)}^{2}} = \sum_{n = 1}^{\infty} n {(- 1)}^{n - 1} u^{n - 1} \Rightarrow$ $\frac{1}{{(1 + t^{2})}^{2}} = \sum_{n = 1}^{\infty} n {(- 1)}^{n - 1} t^{2 n - 2} \Rightarrow f (x) = \int_{0}^{x} e^{t} (\sum_{n = 1}^{\infty} n {(- 1)}^{n - 1} t^{2 n - 2}) dt$ $= \sum_{n = 1}^{\infty} n {(- 1)}^{n - 1} \int_{0}^{x} t^{2 n - 2} e^{t} dt = \sum_{n = 1}^{\infty} n {(- 1)}^{n - 1} U_{n}$ $U_{n} = \int_{0}^{x} t^{2 n - 2} e^{t} dt by parts u^{^{'}} = t^{2 n - 2} and v = e^{t} \Rightarrow$ $U_{n} = {[\frac{1}{2 n - 1} t^{2 n - 1} e^{t}]}_{0}^{x} - \int_{0}^{x} \frac{1}{2 n - 1} t^{2 n - 1} e^{t} dt$ $= \frac{x^{2 n - 1} e^{x}}{2 n - 1} - \frac{1}{2 n - 1} \int_{0}^{x} t^{2 n - 1} e^{t} dt and$ $\int_{0}^{x} t^{2 n - 1} e^{t} dt = {[\frac{t^{2 n}}{2 n} e^{t}]}_{0}^{x} - \int_{0}^{x} \frac{t^{2 n}}{2 n} e^{t} dt = \frac{x^{2 n} e^{x}}{2 n} - \frac{1}{2 n} \int_{0}^{x} t^{2 n} e^{t} dt$ $= \frac{x^{2 n} e^{x}}{2 n} - \frac{1}{2 n} U_{n + 1} \Rightarrow U_{n} = \frac{x^{2 n - 1} e^{x}}{2 n - 1} - \frac{1}{2 n - 1} {\frac{x^{2 n} e^{x}}{2 n} - \frac{1}{2 n} U_{n + 1}}$ $= \frac{x^{2 n - 1} e^{x}}{2 n - 1} - \frac{x^{2 n} e^{x}}{(2 n - 1) (2 n)} + \frac{1}{2 n (2 n - 1)} U_{n + 1}$ $. . . be continued$
	Answered by maths mind last updated on 12/Jul/20
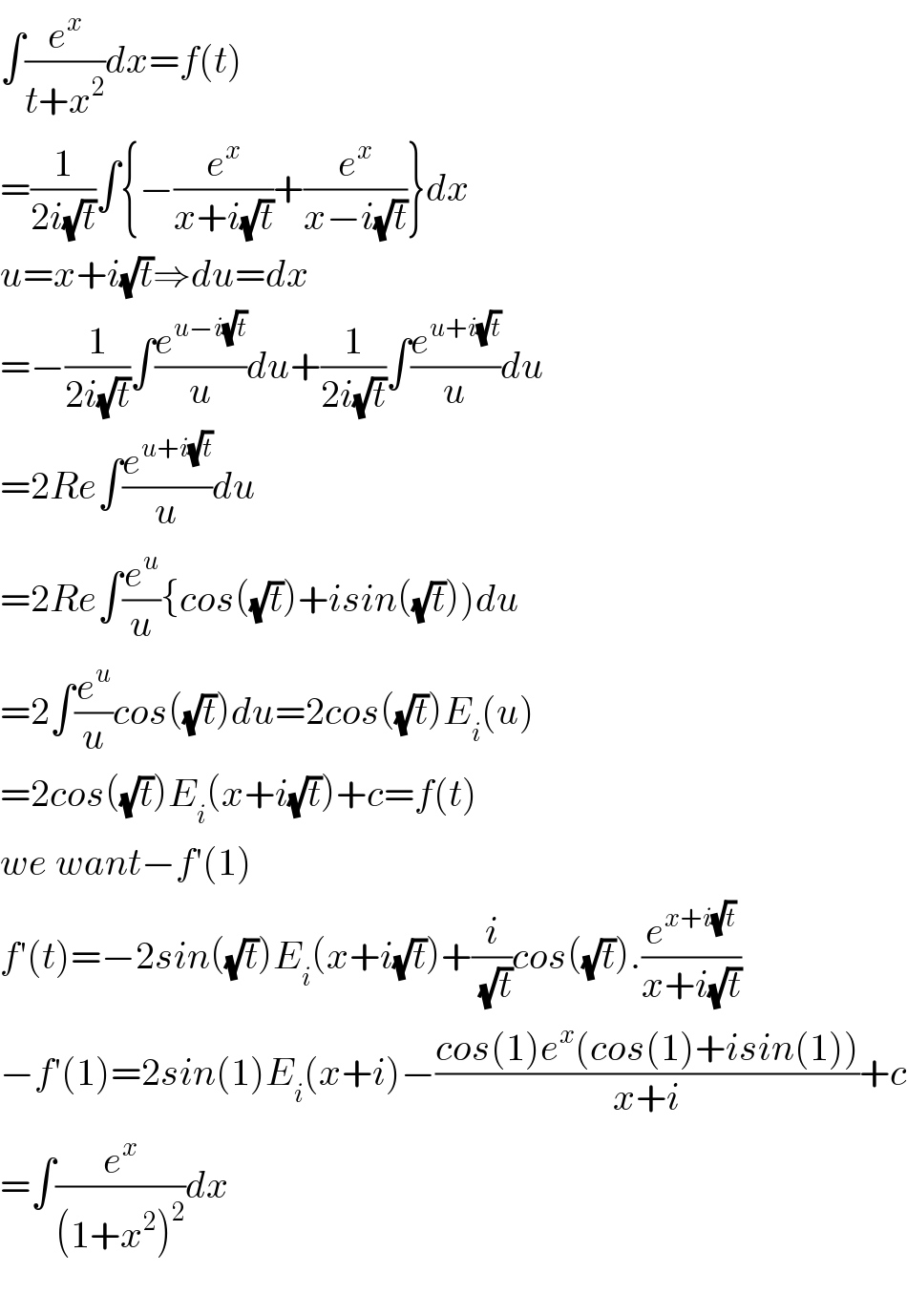
	$∫(e^x /(t+x^2 ))dx=f(t) =(1/(2i(√t)))∫{−(e^x /(x+i(√t)))+(e^x /(x−i(√t)))}dx u=x+i(√t)⇒du=dx =−(1/(2i(√t)))∫(e^(u−i(√t)) /u)du+(1/(2i(√t)))∫(e^(u+i(√t)) /u)du =2Re∫(e^(u+i(√t)) /u)du =2Re∫(e^u /u){cos((√t))+isin((√t)))du =2∫(e^u /u)cos((√t))du=2cos((√t))E_i (u) =2cos((√t))E_i (x+i(√t))+c=f(t) we want−f′(1) f′(t)=−2sin((√t))E_i (x+i(√t))+(i/(√t))cos((√t)).(e^(x+i(√t)) /(x+i(√t))) −f′(1)=2sin(1)E_i (x+i)−((cos(1)e^x (cos(1)+isin(1)))/(x+i))+c =∫(e^x /((1+x^2 )^2 ))dx$
	$\int \frac{e^{x}}{t + x^{2}} d x = f (t)$ $= \frac{1}{2 i \sqrt{t}} \int {- \frac{e^{x}}{x + i \sqrt{t}} + \frac{e^{x}}{x - i \sqrt{t}}} d x$ $u = x + i \sqrt{t} \Rightarrow d u = d x$ $= - \frac{1}{2 i \sqrt{t}} \int \frac{e^{u - i \sqrt{t}}}{u} d u + \frac{1}{2 i \sqrt{t}} \int \frac{e^{u + i \sqrt{t}}}{u} d u$ $= 2 R e \int \frac{e^{u + i \sqrt{t}}}{u} d u$ $= 2 R e \int \frac{e^{u}}{u} {c o s (\sqrt{t}) + i s i n (\sqrt{t})) d u$ $= 2 \int \frac{e^{u}}{u} c o s (\sqrt{t}) d u = 2 c o s (\sqrt{t}) E_{i} (u)$ $= 2 c o s (\sqrt{t}) E_{i} (x + i \sqrt{t}) + c = f (t)$ $w e w a n t - f^{'} (1)$ $f^{'} (t) = - 2 s i n (\sqrt{t}) E_{i} (x + i \sqrt{t}) + \frac{i}{\sqrt{t}} c o s (\sqrt{t}) . \frac{e^{x + i \sqrt{t}}}{x + i \sqrt{t}}$ $- f^{'} (1) = 2 s i n (1) E_{i} (x + i) - \frac{c o s (1) e^{x} (c o s (1) + i s i n (1))}{x + i} + c$ $= \int \frac{e^{x}}{{(1 + x^{2})}^{2}} d x$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum