Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 103021 by dw last updated on 12/Jul/20

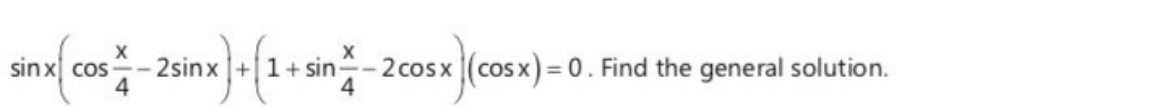
Answered by Dwaipayan Shikari last updated on 12/Jul/20

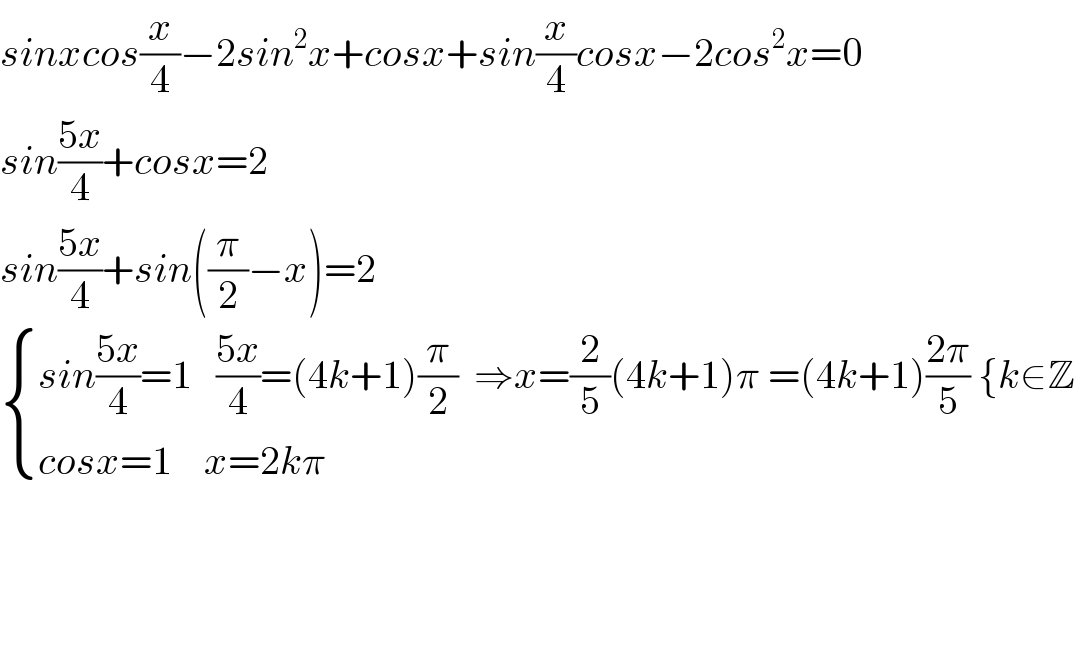
sinxcos(x/4)−2sin^2 x+cosx+sin(x/4)cosx−2cos^2 x=0 sin((5x)/4)+cosx=2 sin((5x)/4)+sin((π/2)−x)=2 { ((sin((5x)/4)=1 ((5x)/4)=(4k+1)(π/2) ⇒x=(2/5)(4k+1)π =(4k+1)((2π)/5) {k∈Z)),((cosx=1 x=2kπ)) :}

$${sinxcos}\frac{{x}}{\mathrm{4}}−\mathrm{2}{sin}^{\mathrm{2}} {x}+{cosx}+{sin}\frac{{x}}{\mathrm{4}}{cosx}−\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$${sin}\frac{\mathrm{5}{x}}{\mathrm{4}}+{cosx}=\mathrm{2} \\ $$$${sin}\frac{\mathrm{5}{x}}{\mathrm{4}}+{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)=\mathrm{2} \\ $$$$\begin{cases}{{sin}\frac{\mathrm{5}{x}}{\mathrm{4}}=\mathrm{1}\:\:\:\frac{\mathrm{5}{x}}{\mathrm{4}}=\left(\mathrm{4}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\:\:\Rightarrow{x}=\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{4}{k}+\mathrm{1}\right)\pi\:=\left(\mathrm{4}{k}+\mathrm{1}\right)\frac{\mathrm{2}\pi}{\mathrm{5}}\:\left\{{k}\in\mathbb{Z}\right.}\\{{cosx}=\mathrm{1}\:\:\:\:{x}=\mathrm{2}{k}\pi}\end{cases} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$

Answered by 1549442205 last updated on 13/Jul/20

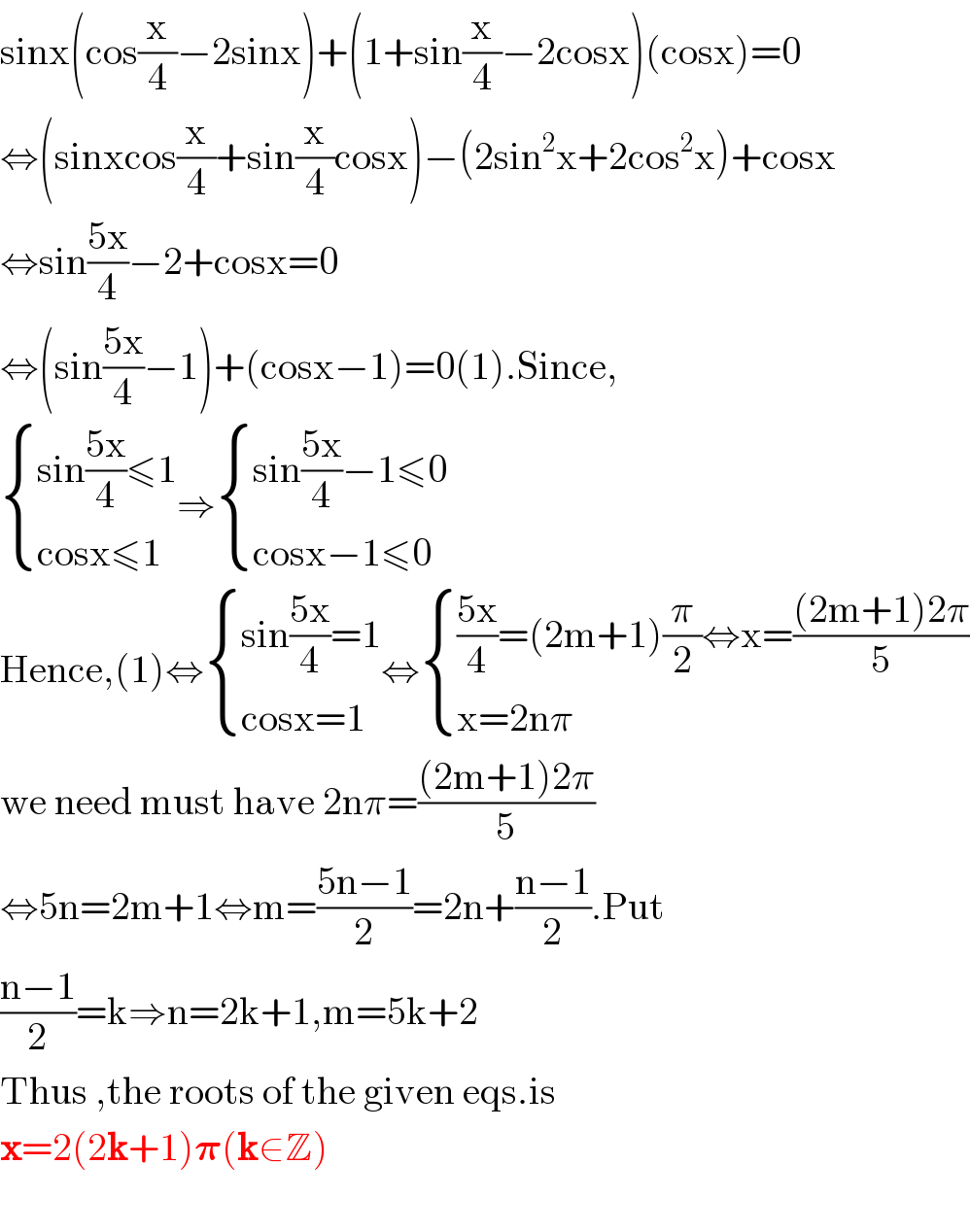
sinx(cos(x/4)−2sinx)+(1+sin(x/4)−2cosx)(cosx)=0 ⇔(sinxcos(x/4)+sin(x/4)cosx)−(2sin^2 x+2cos^2 x)+cosx ⇔sin((5x)/4)−2+cosx=0 ⇔(sin((5x)/4)−1)+(cosx−1)=0(1).Since, { ((sin((5x)/4)≤1)),((cosx≤1)) :}⇒ { ((sin((5x)/4)−1≤0)),((cosx−1≤0)) :} Hence,(1)⇔ { ((sin((5x)/4)=1)),((cosx=1)) :}⇔ { ((((5x)/4)=(2m+1)(π/2)⇔x=(((2m+1)2π)/5))),((x=2nπ)) :} we need must have 2nπ=(((2m+1)2π)/5) ⇔5n=2m+1⇔m=((5n−1)/2)=2n+((n−1)/2).Put ((n−1)/2)=k⇒n=2k+1,m=5k+2 Thus ,the roots of the given eqs.is x=2(2k+1)𝛑(k∈Z)

$$\mathrm{sinx}\left(\mathrm{cos}\frac{\mathrm{x}}{\mathrm{4}}−\mathrm{2sinx}\right)+\left(\mathrm{1}+\mathrm{sin}\frac{\mathrm{x}}{\mathrm{4}}−\mathrm{2cosx}\right)\left(\mathrm{cosx}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{sinxcos}\frac{\mathrm{x}}{\mathrm{4}}+\mathrm{sin}\frac{\mathrm{x}}{\mathrm{4}}\mathrm{cosx}\right)−\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{x}+\mathrm{2cos}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{cosx} \\ $$$$\Leftrightarrow\mathrm{sin}\frac{\mathrm{5x}}{\mathrm{4}}−\mathrm{2}+\mathrm{cosx}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{sin}\frac{\mathrm{5x}}{\mathrm{4}}−\mathrm{1}\right)+\left(\mathrm{cosx}−\mathrm{1}\right)=\mathrm{0}\left(\mathrm{1}\right).\mathrm{Since}, \\ $$$$\begin{cases}{\mathrm{sin}\frac{\mathrm{5x}}{\mathrm{4}}\leqslant\mathrm{1}}\\{\mathrm{cosx}\leqslant\mathrm{1}}\end{cases}\Rightarrow\begin{cases}{\mathrm{sin}\frac{\mathrm{5x}}{\mathrm{4}}−\mathrm{1}\leqslant\mathrm{0}}\\{\mathrm{cosx}−\mathrm{1}\leqslant\mathrm{0}}\end{cases} \\ $$$$\mathrm{Hence},\left(\mathrm{1}\right)\Leftrightarrow\begin{cases}{\mathrm{sin}\frac{\mathrm{5x}}{\mathrm{4}}=\mathrm{1}}\\{\mathrm{cosx}=\mathrm{1}}\end{cases}\Leftrightarrow\begin{cases}{\frac{\mathrm{5x}}{\mathrm{4}}=\left(\mathrm{2m}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\Leftrightarrow\mathrm{x}=\frac{\left(\mathrm{2m}+\mathrm{1}\right)\mathrm{2}\pi}{\mathrm{5}}}\\{\mathrm{x}=\mathrm{2n}\pi}\end{cases} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{must}\:\mathrm{have}\:\mathrm{2n}\pi=\frac{\left(\mathrm{2m}+\mathrm{1}\right)\mathrm{2}\pi}{\mathrm{5}} \\ $$$$\Leftrightarrow\mathrm{5n}=\mathrm{2m}+\mathrm{1}\Leftrightarrow\mathrm{m}=\frac{\mathrm{5n}−\mathrm{1}}{\mathrm{2}}=\mathrm{2n}+\frac{\mathrm{n}−\mathrm{1}}{\mathrm{2}}.\mathrm{Put} \\ $$$$\frac{\mathrm{n}−\mathrm{1}}{\mathrm{2}}=\mathrm{k}\Rightarrow\mathrm{n}=\mathrm{2k}+\mathrm{1},\mathrm{m}=\mathrm{5k}+\mathrm{2} \\ $$$$\mathrm{Thus}\:,\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{eqs}.\mathrm{is} \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{2}\left(\mathrm{2}\boldsymbol{\mathrm{k}}+\mathrm{1}\right)\boldsymbol{\pi}\left(\boldsymbol{\mathrm{k}}\in\mathbb{Z}\right) \\ $$$$ \\ $$

Commented by dw last updated on 16/Jul/20

Thank you Sir.

$${Thank}\:{you}\:{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com