Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 103124 by Faetma last updated on 12/Jul/20

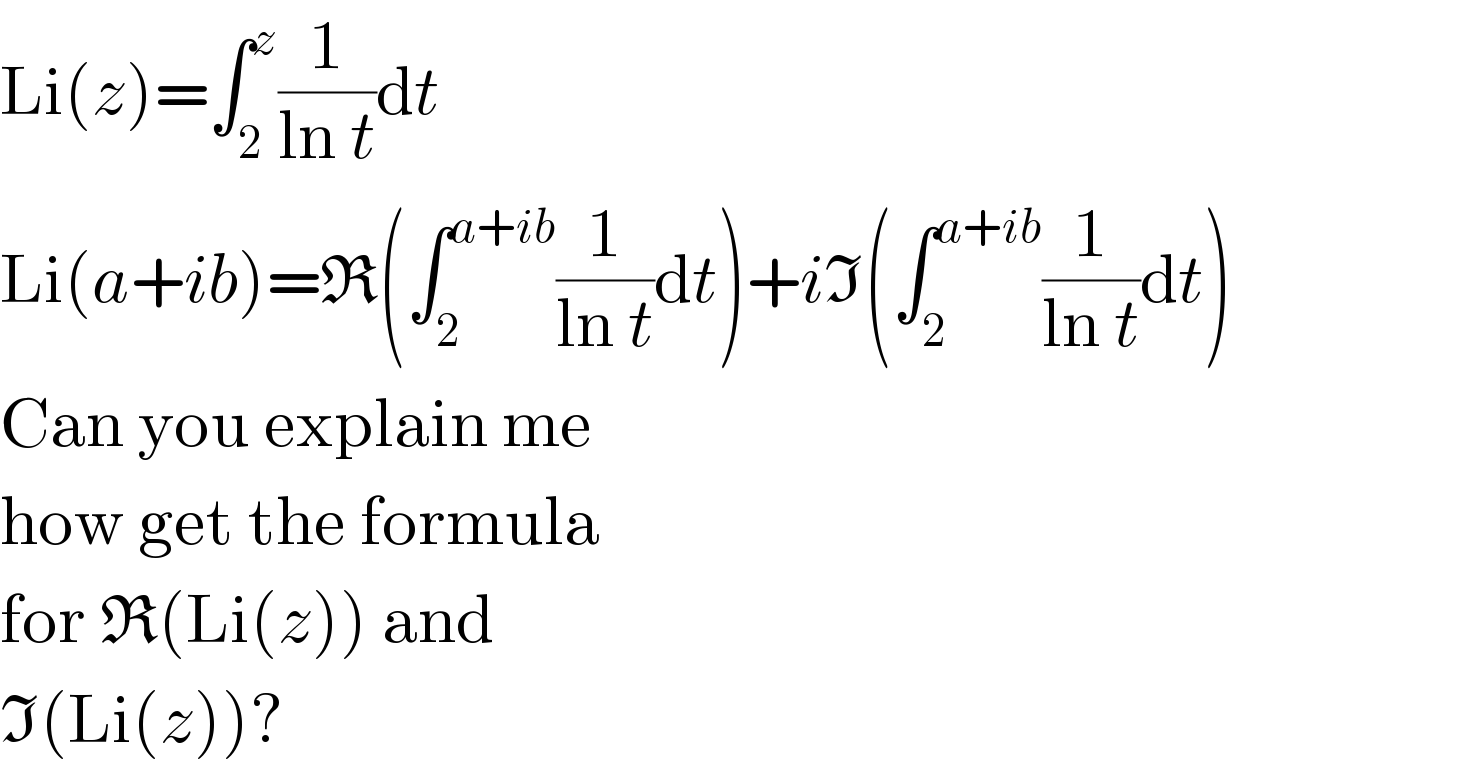
Li(z)=∫_2 ^z (1/(ln t))dt Li(a+ib)=R(∫_2 ^(a+ib) (1/(ln t))dt)+iI(∫_2 ^(a+ib) (1/(ln t))dt) Can you explain me how get the formula for R(Li(z)) and I(Li(z))?

$$\mathrm{Li}\left({z}\right)=\int_{\mathrm{2}} ^{{z}} \frac{\mathrm{1}}{\mathrm{ln}\:{t}}\mathrm{d}{t} \\ $$$$\mathrm{Li}\left({a}+{ib}\right)=\mathfrak{R}\left(\int_{\mathrm{2}} ^{{a}+{ib}} \frac{\mathrm{1}}{\mathrm{ln}\:{t}}\mathrm{d}{t}\right)+{i}\mathfrak{I}\left(\int_{\mathrm{2}} ^{{a}+{ib}} \frac{\mathrm{1}}{\mathrm{ln}\:{t}}\mathrm{d}{t}\right) \\ $$$$\mathrm{Can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{me} \\ $$$$\mathrm{how}\:\mathrm{get}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\mathrm{for}\:\mathfrak{R}\left(\mathrm{Li}\left({z}\right)\right)\:\mathrm{and} \\ $$$$\mathfrak{I}\left(\mathrm{Li}\left({z}\right)\right)? \\ $$

Answered by mathmax by abdo last updated on 13/Jul/20

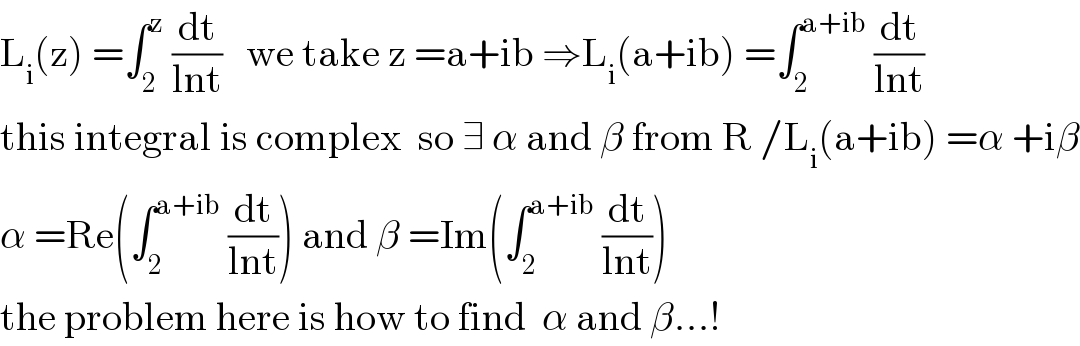
L_i (z) =∫_2 ^z (dt/(lnt)) we take z =a+ib ⇒L_i (a+ib) =∫_2 ^(a+ib) (dt/(lnt)) this integral is complex so ∃ α and β from R /L_i (a+ib) =α +iβ α =Re(∫_2 ^(a+ib) (dt/(lnt))) and β =Im(∫_2 ^(a+ib) (dt/(lnt))) the problem here is how to find α and β...!

$$\mathrm{L}_{\mathrm{i}} \left(\mathrm{z}\right)\:=\int_{\mathrm{2}} ^{\mathrm{z}} \:\frac{\mathrm{dt}}{\mathrm{lnt}}\:\:\:\mathrm{we}\:\mathrm{take}\:\mathrm{z}\:=\mathrm{a}+\mathrm{ib}\:\Rightarrow\mathrm{L}_{\mathrm{i}} \left(\mathrm{a}+\mathrm{ib}\right)\:=\int_{\mathrm{2}} ^{\mathrm{a}+\mathrm{ib}} \:\frac{\mathrm{dt}}{\mathrm{lnt}} \\ $$$$\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{complex}\:\:\mathrm{so}\:\exists\:\alpha\:\mathrm{and}\:\beta\:\mathrm{from}\:\mathrm{R}\:/\mathrm{L}_{\mathrm{i}} \left(\mathrm{a}+\mathrm{ib}\right)\:=\alpha\:+\mathrm{i}\beta \\ $$$$\alpha\:=\mathrm{Re}\left(\int_{\mathrm{2}} ^{\mathrm{a}+\mathrm{ib}} \:\frac{\mathrm{dt}}{\mathrm{lnt}}\right)\:\mathrm{and}\:\beta\:=\mathrm{Im}\left(\int_{\mathrm{2}} ^{\mathrm{a}+\mathrm{ib}} \:\frac{\mathrm{dt}}{\mathrm{lnt}}\right) \\ $$$$\mathrm{the}\:\mathrm{problem}\:\mathrm{here}\:\mathrm{is}\:\mathrm{how}\:\mathrm{to}\:\mathrm{find}\:\:\alpha\:\mathrm{and}\:\beta...! \\ $$

Commented by mathmax by abdo last updated on 13/Jul/20

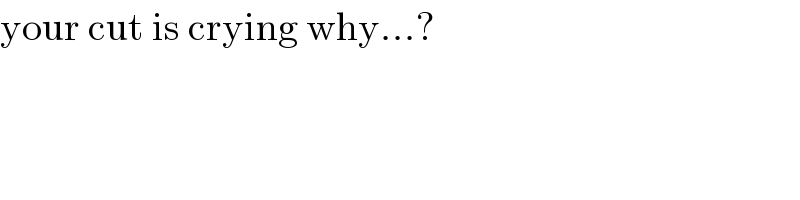
your cut is crying why...?

$$\mathrm{your}\:\mathrm{cut}\:\mathrm{is}\:\mathrm{crying}\:\mathrm{why}...? \\ $$

Commented by Faetma last updated on 13/Jul/20

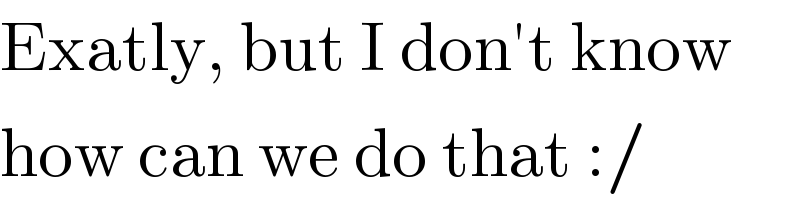
Exatly, but I don′t know how can we do that :/

$$\mathrm{Exatly},\:\mathrm{but}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know} \\ $$$$\mathrm{how}\:\mathrm{can}\:\mathrm{we}\:\mathrm{do}\:\mathrm{that}\::/ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com