Question Number 103130 by chamkunda last updated on 13/Jul/20

find out the fourth member of the following formula after expansion [πx+(2/x)]^8

Commented bychamkunda last updated on 13/Jul/20

please can someone help and answer this find out the fourth member of the following formula after expansion [πx+(2/x)]^8 find out the fourth member of the following formula after expansion [πx+(2/x)]^8

Answered by floor(10²Eta[1]) last updated on 13/Jul/20

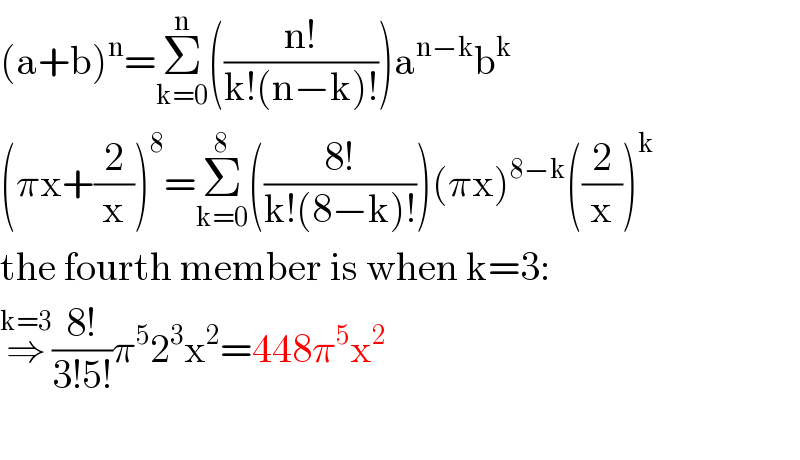
(a+b)^n =Σ_(k=0) ^n (((n!)/(k!(n−k)!)))a^(n−k) b^k (πx+(2/x))^8 =Σ_(k=0) ^8 (((8!)/(k!(8−k)!)))(πx)^(8−k) ((2/x))^k the fourth member is when k=3: ⇒^(k=3) ((8!)/(3!5!))π^5 2^3 x^2 =448π^5 x^2

Answered by bemath last updated on 13/Jul/20

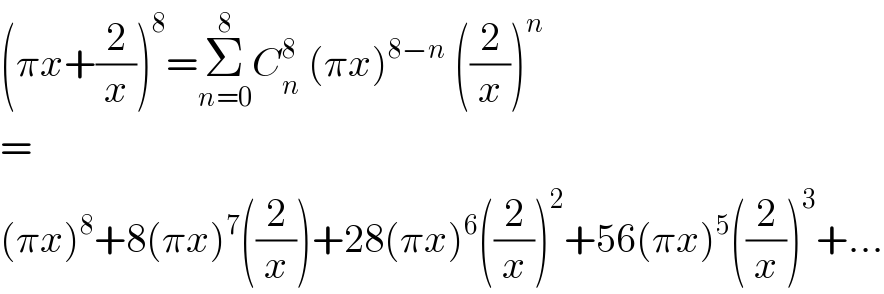
(πx+(2/x))^8 =Σ_(n=0) ^8 C_n ^8 (πx)^(8−n) ((2/x))^n = (πx)^8 +8(πx)^7 ((2/x))+28(πx)^6 ((2/x))^2 +56(πx)^5 ((2/x))^3 +...

Commented by1549442205 last updated on 13/Jul/20

I agree to this expansion a_3 =((8!)/(2!6!))π^6 x^6 ×(4/x^2 ) =112𝛑^6 x^4 ,excuse me a_4 =448𝛑^5 x^2 as above

Commented byfloor(10²Eta[1]) last updated on 13/Jul/20

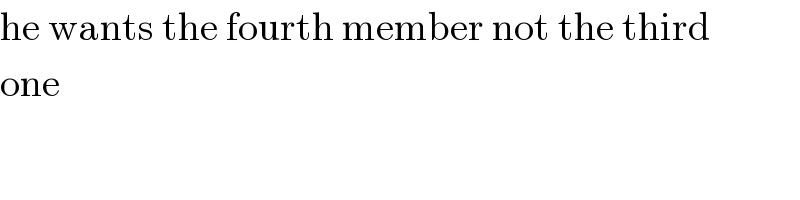
he wants the fourth member not the third one

Answered by OlafThorendsen last updated on 13/Jul/20

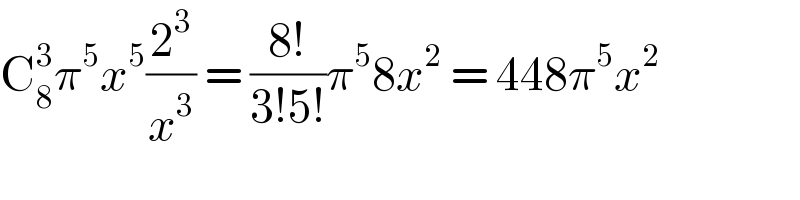
C_8 ^3 π^5 x^5 (2^3 /x^3 ) = ((8!)/(3!5!))π^5 8x^2 = 448π^5 x^2