Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 103147 by ajfour last updated on 13/Jul/20

Answered by mr W last updated on 13/Jul/20

A(a,0) B(0,(√(p^2 −a^2 ))) C(0,c) D((√(q^2 −c^2 )),0) a(√(p^2 −a^2 ))=c(√(q^2 −c^2 )) ...(i) intersection AB and CD at (h,k) (h/a)+(k/(√(p^2 −a^2 )))=1 (h/(√(q^2 −c^2 )))+(k/c)=1 ((1/(ac))−(1/(√((p^2 −a^2 )(q^2 −c^2 )))))h=(1/c)−(1/(√(p^2 −a^2 ))) ⇒h=(((1/c)−(1/(√(p^2 −a^2 ))))/((1/(ac))−(1/(√((p^2 −a^2 )(q^2 −c^2 )))))) (c−(√(p^2 −a^2 )))h=(1/2)c(√(q^2 −c^2 )) ⇒(c−(√(p^2 −a^2 )))(((1/c)−(1/(√(p^2 −a^2 ))))/((1/(ac))−(1/(√((p^2 −a^2 )(q^2 −c^2 ))))))=(1/2)c(√(q^2 −c^2 )) ...(ii) from (i): c^4 −q^2 c^2 +a^2 (p^2 −a^2 )=0 c^2 =((q^2 +(√(q^4 −4a^2 (p^2 −a^2 ))))/2) c=(√((q^2 +(√(q^4 −4a^2 (p^2 −a^2 ))))/2)) put this into (ii) to find a...

$${A}\left({a},\mathrm{0}\right) \\ $$$${B}\left(\mathrm{0},\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right) \\ $$$${C}\left(\mathrm{0},{c}\right) \\ $$$${D}\left(\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} },\mathrm{0}\right) \\ $$$${a}\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }={c}\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:\:\:...\left({i}\right) \\ $$$${intersection}\:{AB}\:{and}\:{CD}\:{at}\:\left({h},{k}\right) \\ $$$$\frac{{h}}{{a}}+\frac{{k}}{\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }}=\mathrm{1} \\ $$$$\frac{{h}}{\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }}+\frac{{k}}{{c}}=\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}}{{ac}}−\frac{\mathrm{1}}{\sqrt{\left({p}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({q}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}}\right){h}=\frac{\mathrm{1}}{{c}}−\frac{\mathrm{1}}{\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }} \\ $$$$\Rightarrow{h}=\frac{\frac{\mathrm{1}}{{c}}−\frac{\mathrm{1}}{\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }}}{\frac{\mathrm{1}}{{ac}}−\frac{\mathrm{1}}{\sqrt{\left({p}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({q}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}}} \\ $$$$\left({c}−\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right){h}=\frac{\mathrm{1}}{\mathrm{2}}{c}\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\Rightarrow\left({c}−\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right)\frac{\frac{\mathrm{1}}{{c}}−\frac{\mathrm{1}}{\sqrt{{p}^{\mathrm{2}} −{a}^{\mathrm{2}} }}}{\frac{\mathrm{1}}{{ac}}−\frac{\mathrm{1}}{\sqrt{\left({p}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({q}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}}}=\frac{\mathrm{1}}{\mathrm{2}}{c}\sqrt{{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:\:\:...\left({ii}\right) \\ $$$${from}\:\left({i}\right): \\ $$$${c}^{\mathrm{4}} −{q}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({p}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${c}^{\mathrm{2}} =\frac{{q}^{\mathrm{2}} +\sqrt{{q}^{\mathrm{4}} −\mathrm{4}{a}^{\mathrm{2}} \left({p}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$${c}=\sqrt{\frac{{q}^{\mathrm{2}} +\sqrt{{q}^{\mathrm{4}} −\mathrm{4}{a}^{\mathrm{2}} \left({p}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}}{\mathrm{2}}} \\ $$$${put}\:{this}\:{into}\:\left({ii}\right)\:{to}\:{find}\:{a}... \\ $$

Commented by mr W last updated on 13/Jul/20

Commented by ajfour last updated on 13/Jul/20

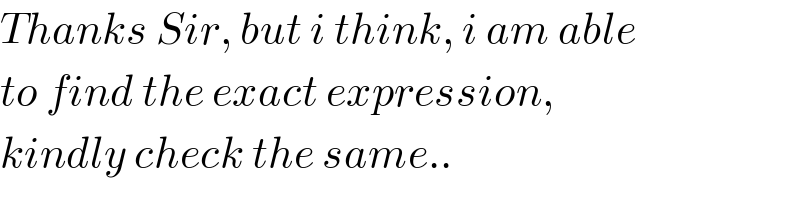
Thanks Sir, but i think, i am able to find the exact expression, kindly check the same..

$${Thanks}\:{Sir},\:{but}\:{i}\:{think},\:{i}\:{am}\:{able} \\ $$$${to}\:{find}\:{the}\:{exact}\:{expression}, \\ $$$${kindly}\:{check}\:{the}\:{same}.. \\ $$

Answered by ajfour last updated on 13/Jul/20

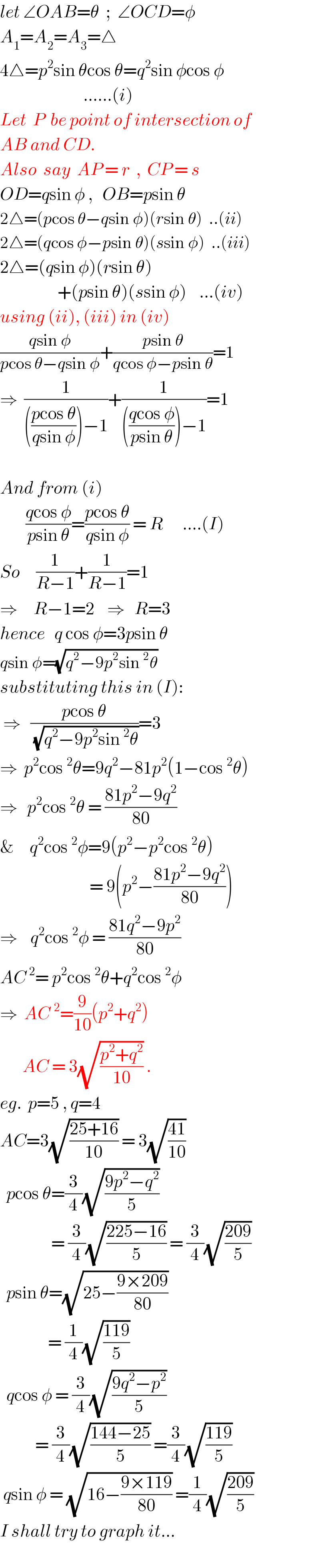
let ∠OAB=θ ; ∠OCD=φ A_1 =A_2 =A_3 =△ 4△=p^2 sin θcos θ=q^2 sin φcos φ ......(i) Let P be point of intersection of AB and CD. Also say AP = r , CP = s OD=qsin φ , OB=psin θ 2△=(pcos θ−qsin φ)(rsin θ) ..(ii) 2△=(qcos φ−psin θ)(ssin φ) ..(iii) 2△=(qsin φ)(rsin θ) +(psin θ)(ssin φ) ...(iv) using (ii), (iii) in (iv) ((qsin φ)/(pcos θ−qsin φ))+((psin θ)/(qcos φ−psin θ))=1 ⇒ (1/((((pcos θ)/(qsin φ)))−1))+(1/((((qcos φ)/(psin θ)))−1))=1 And from (i) ((qcos φ)/(psin θ))=((pcos θ)/(qsin φ)) = R ....(I) So (1/(R−1))+(1/(R−1))=1 ⇒ R−1=2 ⇒ R=3 hence q cos φ=3psin θ qsin φ=(√(q^2 −9p^2 sin^2 θ)) substituting this in (I): ⇒ ((pcos θ)/(√(q^2 −9p^2 sin^2 θ)))=3 ⇒ p^2 cos^2 θ=9q^2 −81p^2 (1−cos^2 θ) ⇒ p^2 cos^2 θ = ((81p^2 −9q^2 )/(80)) & q^2 cos^2 φ=9(p^2 −p^2 cos^2 θ) = 9(p^2 −((81p^2 −9q^2 )/(80))) ⇒ q^2 cos^2 φ = ((81q^2 −9p^2 )/(80)) AC^( 2) = p^2 cos^2 θ+q^2 cos^2 φ ⇒ AC^2 =(9/(10))(p^2 +q^2 ) AC = 3(√((p^2 +q^2 )/(10))) . eg. p=5 , q=4 AC=3(√((25+16)/(10))) = 3(√((41)/(10))) pcos θ=(3/4)(√((9p^2 −q^2 )/5)) = (3/4)(√((225−16)/5)) = (3/4)(√((209)/5)) psin θ=(√(25−((9×209)/(80)))) = (1/4)(√((119)/5)) qcos φ = (3/4)(√((9q^2 −p^2 )/5)) = (3/4)(√((144−25)/5)) =(3/4)(√((119)/5)) qsin φ = (√(16−((9×119)/(80)))) =(1/4)(√((209)/5)) I shall try to graph it...

$${let}\:\angle{OAB}=\theta\:\:;\:\:\angle{OCD}=\phi \\ $$$${A}_{\mathrm{1}} ={A}_{\mathrm{2}} ={A}_{\mathrm{3}} =\bigtriangleup \\ $$$$\mathrm{4}\bigtriangleup={p}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta={q}^{\mathrm{2}} \mathrm{sin}\:\phi\mathrm{cos}\:\phi\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......\left({i}\right) \\ $$$${Let}\:\:{P}\:\:{be}\:{point}\:{of}\:{intersection}\:{of} \\ $$$${AB}\:{and}\:{CD}. \\ $$$${Also}\:\:{say}\:\:{AP}\:=\:{r}\:\:,\:\:{CP}\:=\:{s} \\ $$$${OD}={q}\mathrm{sin}\:\phi\:,\:\:\:{OB}={p}\mathrm{sin}\:\theta \\ $$$$\mathrm{2}\bigtriangleup=\left({p}\mathrm{cos}\:\theta−{q}\mathrm{sin}\:\phi\right)\left({r}\mathrm{sin}\:\theta\right)\:\:..\left({ii}\right) \\ $$$$\mathrm{2}\bigtriangleup=\left({q}\mathrm{cos}\:\phi−{p}\mathrm{sin}\:\theta\right)\left({s}\mathrm{sin}\:\phi\right)\:\:..\left({iii}\right) \\ $$$$\mathrm{2}\bigtriangleup=\left({q}\mathrm{sin}\:\phi\right)\left({r}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({p}\mathrm{sin}\:\theta\right)\left({s}\mathrm{sin}\:\phi\right)\:\:\:\:...\left({iv}\right) \\ $$$${using}\:\left({ii}\right),\:\left({iii}\right)\:{in}\:\left({iv}\right) \\ $$$$\frac{{q}\mathrm{sin}\:\phi}{{p}\mathrm{cos}\:\theta−{q}\mathrm{sin}\:\phi}+\frac{{p}\mathrm{sin}\:\theta}{{q}\mathrm{cos}\:\phi−{p}\mathrm{sin}\:\theta}=\mathrm{1} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\left(\frac{{p}\mathrm{cos}\:\theta}{{q}\mathrm{sin}\:\phi}\right)−\mathrm{1}}+\frac{\mathrm{1}}{\left(\frac{{q}\mathrm{cos}\:\phi}{{p}\mathrm{sin}\:\theta}\right)−\mathrm{1}}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${And}\:{from}\:\left({i}\right)\:\: \\ $$$$\:\:\:\:\:\:\:\:\frac{{q}\mathrm{cos}\:\phi}{{p}\mathrm{sin}\:\theta}=\frac{{p}\mathrm{cos}\:\theta}{{q}\mathrm{sin}\:\phi}\:=\:{R}\:\:\:\:\:\:....\left({I}\right) \\ $$$${So}\:\:\:\:\:\frac{\mathrm{1}}{{R}−\mathrm{1}}+\frac{\mathrm{1}}{{R}−\mathrm{1}}=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\:{R}−\mathrm{1}=\mathrm{2}\:\:\:\:\Rightarrow\:\:\:{R}=\mathrm{3} \\ $$$${hence}\:\:\:{q}\:\mathrm{cos}\:\phi=\mathrm{3}{p}\mathrm{sin}\:\theta \\ $$$${q}\mathrm{sin}\:\phi=\sqrt{{q}^{\mathrm{2}} −\mathrm{9}{p}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$${substituting}\:{this}\:{in}\:\left({I}\right): \\ $$$$\:\Rightarrow\:\:\:\frac{{p}\mathrm{cos}\:\theta}{\sqrt{{q}^{\mathrm{2}} −\mathrm{9}{p}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}}=\mathrm{3} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta=\mathrm{9}{q}^{\mathrm{2}} −\mathrm{81}{p}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\Rightarrow\:\:\:{p}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\:=\:\frac{\mathrm{81}{p}^{\mathrm{2}} −\mathrm{9}{q}^{\mathrm{2}} }{\mathrm{80}} \\ $$$$\&\:\:\:\:\:{q}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi=\mathrm{9}\left({p}^{\mathrm{2}} −{p}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{9}\left({p}^{\mathrm{2}} −\frac{\mathrm{81}{p}^{\mathrm{2}} −\mathrm{9}{q}^{\mathrm{2}} }{\mathrm{80}}\right) \\ $$$$\Rightarrow\:\:\:\:{q}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi\:=\:\frac{\mathrm{81}{q}^{\mathrm{2}} −\mathrm{9}{p}^{\mathrm{2}} }{\mathrm{80}} \\ $$$${AC}^{\:\mathrm{2}} =\:{p}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{q}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi \\ $$$$\Rightarrow\:\:{AC}\:^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{10}}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:{AC}\:=\:\mathrm{3}\sqrt{\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }{\mathrm{10}}}\:. \\ $$$${eg}.\:\:{p}=\mathrm{5}\:,\:{q}=\mathrm{4} \\ $$$${AC}=\mathrm{3}\sqrt{\frac{\mathrm{25}+\mathrm{16}}{\mathrm{10}}}\:=\:\mathrm{3}\sqrt{\frac{\mathrm{41}}{\mathrm{10}}} \\ $$$$\:\:{p}\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\frac{\mathrm{9}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{5}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\frac{\mathrm{225}−\mathrm{16}}{\mathrm{5}}}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\frac{\mathrm{209}}{\mathrm{5}}} \\ $$$$\:\:{p}\mathrm{sin}\:\theta=\sqrt{\mathrm{25}−\frac{\mathrm{9}×\mathrm{209}}{\mathrm{80}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\frac{\mathrm{119}}{\mathrm{5}}} \\ $$$$\:\:{q}\mathrm{cos}\:\phi\:=\:\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\frac{\mathrm{9}{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{5}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\frac{\mathrm{144}−\mathrm{25}}{\mathrm{5}}}\:=\frac{\mathrm{3}}{\mathrm{4}}\sqrt{\frac{\mathrm{119}}{\mathrm{5}}} \\ $$$$\:{q}\mathrm{sin}\:\phi\:=\:\sqrt{\mathrm{16}−\frac{\mathrm{9}×\mathrm{119}}{\mathrm{80}}}\:=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\frac{\mathrm{209}}{\mathrm{5}}} \\ $$$${I}\:{shall}\:{try}\:{to}\:{graph}\:{it}... \\ $$$$ \\ $$

Commented by ajfour last updated on 13/Jul/20

Commented by mr W last updated on 13/Jul/20

fantastically solved!

$${fantastically}\:{solved}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com