Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 103190 by bemath last updated on 13/Jul/20

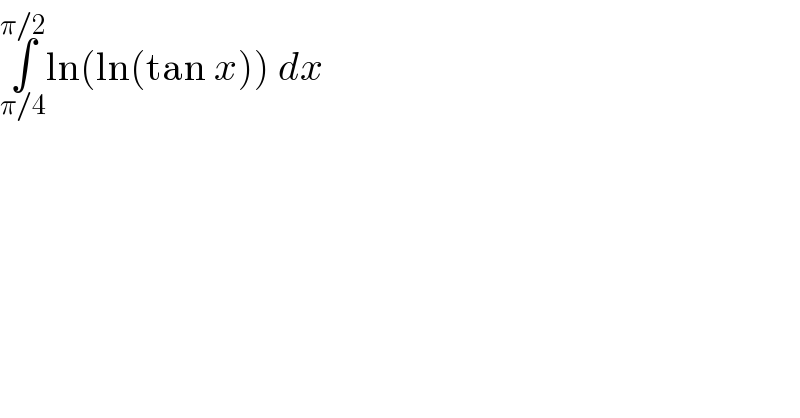
∫_(π/4) ^(π/2) ln(ln(tan x)) dx

$$\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{ln}\left(\mathrm{ln}\left(\mathrm{tan}\:{x}\right)\right)\:{dx}\: \\ $$

Answered by abdomathmax last updated on 13/Jul/20

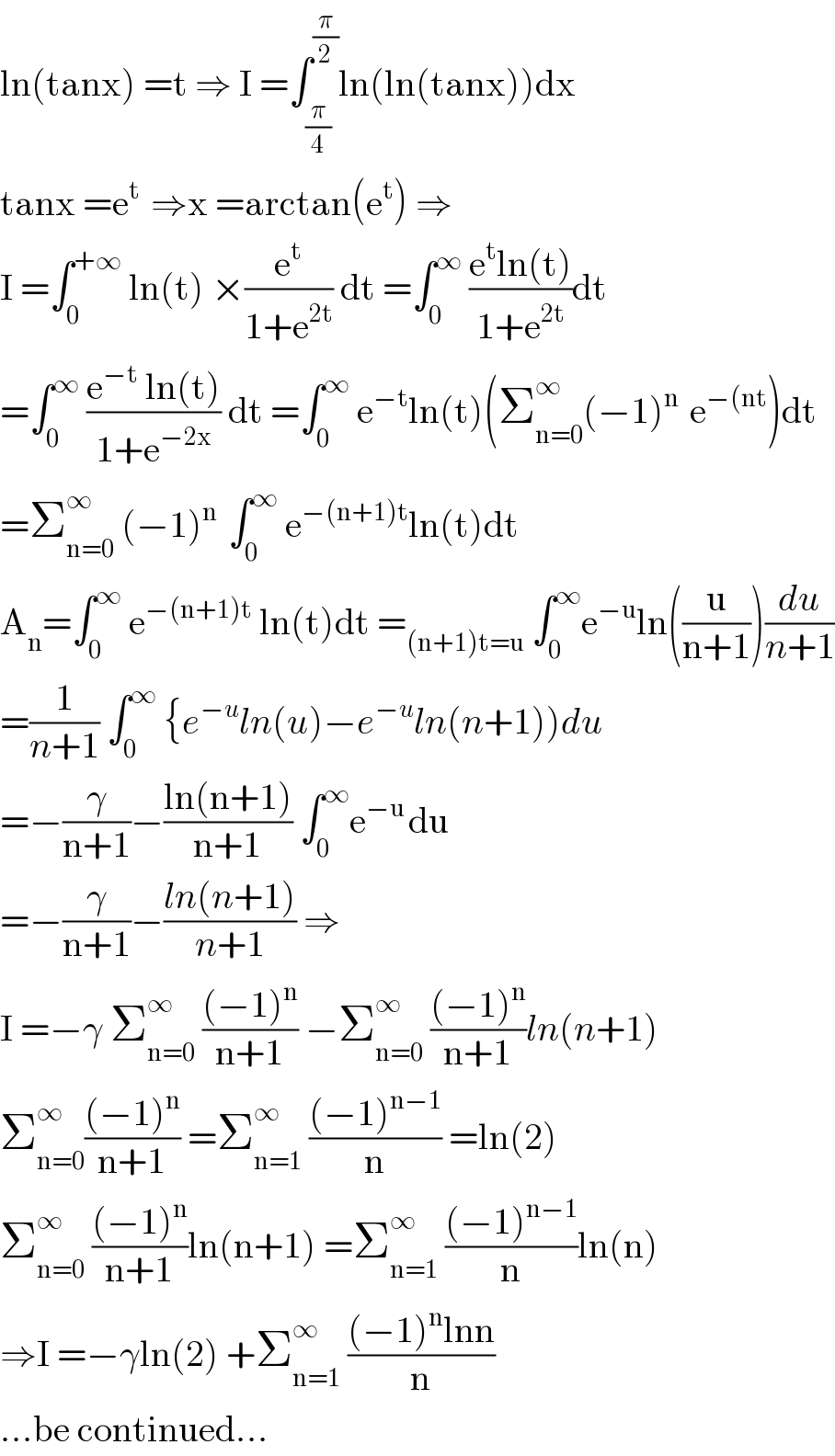
ln(tanx) =t ⇒ I =∫_(π/4) ^(π/2) ln(ln(tanx))dx tanx =e^(t ) ⇒x =arctan(e^t ) ⇒ I =∫_0 ^(+∞) ln(t) ×(e^t /(1+e^(2t) )) dt =∫_0 ^∞ ((e^t ln(t))/(1+e^(2t) ))dt =∫_0 ^∞ ((e^(−t) ln(t))/(1+e^(−2x) )) dt =∫_0 ^∞ e^(−t) ln(t)(Σ_(n=0) ^(∞ ) (−1)^(n ) e^(−(nt) )dt =Σ_(n=0) ^∞ (−1)^(n ) ∫_0 ^∞ e^(−(n+1)t) ln(t)dt A_n =∫_0 ^∞ e^(−(n+1)t) ln(t)dt =_((n+1)t=u) ∫_0 ^∞ e^(−u) ln((u/(n+1)))(du/(n+1)) =(1/(n+1)) ∫_0 ^∞ {e^(−u) ln(u)−e^(−u) ln(n+1))du =−(γ/(n+1))−((ln(n+1))/(n+1)) ∫_0 ^∞ e^(−u ) du =−(γ/(n+1))−((ln(n+1))/(n+1)) ⇒ I =−γ Σ_(n=0) ^(∞ ) (((−1)^n )/(n+1)) −Σ_(n=0) ^∞ (((−1)^n )/(n+1))ln(n+1) Σ_(n=0) ^∞ (((−1)^n )/(n+1)) =Σ_(n=1) ^(∞ ) (((−1)^(n−1) )/n) =ln(2) Σ_(n=0) ^∞ (((−1)^n )/(n+1))ln(n+1) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)ln(n) ⇒I =−γln(2) +Σ_(n=1) ^∞ (((−1)^n lnn)/n) ...be continued...

$$\mathrm{ln}\left(\mathrm{tanx}\right)\:=\mathrm{t}\:\Rightarrow\:\mathrm{I}\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{ln}\left(\mathrm{tanx}\right)\right)\mathrm{dx} \\ $$$$\mathrm{tanx}\:=\mathrm{e}^{\mathrm{t}\:} \:\Rightarrow\mathrm{x}\:=\mathrm{arctan}\left(\mathrm{e}^{\mathrm{t}} \right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{+\infty} \:\mathrm{ln}\left(\mathrm{t}\right)\:×\frac{\mathrm{e}^{\mathrm{t}} }{\mathrm{1}+\mathrm{e}^{\mathrm{2t}} }\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{e}^{\mathrm{2t}} }\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} \:\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{e}^{−\mathrm{2x}} }\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \left(−\mathrm{1}\right)^{\mathrm{n}\:} \:\mathrm{e}^{−\left(\mathrm{nt}\right.} \right)\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}\:} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:=_{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}=\mathrm{u}} \:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}} \mathrm{ln}\left(\frac{\mathrm{u}}{\mathrm{n}+\mathrm{1}}\right)\frac{{du}}{{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\left\{{e}^{−{u}} {ln}\left({u}\right)−{e}^{−{u}} {ln}\left({n}+\mathrm{1}\right)\right){du} \\ $$$$=−\frac{\gamma}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{ln}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}\:} \mathrm{du} \\ $$$$=−\frac{\gamma}{\mathrm{n}+\mathrm{1}}−\frac{{ln}\left({n}+\mathrm{1}\right)}{{n}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}\:=−\gamma\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\:−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}{ln}\left({n}+\mathrm{1}\right) \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:=\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{n}+\mathrm{1}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{ln}\left(\mathrm{n}\right) \\ $$$$\Rightarrow\mathrm{I}\:=−\gamma\mathrm{ln}\left(\mathrm{2}\right)\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{lnn}}{\mathrm{n}} \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$

Commented by abdomathmax last updated on 13/Jul/20

i dont remember the value of Σ_(n=1) ^∞ (((−1)^n ln(n))/n) take a look at the platform...

$$\mathrm{i}\:\mathrm{dont}\:\mathrm{remember}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{n}} \\ $$$$\mathrm{take}\:\mathrm{a}\:\mathrm{look}\:\mathrm{at}\:\mathrm{the}\:\mathrm{platform}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com