
Question Number 103205 by DGmichael last updated on 13/Jul/20
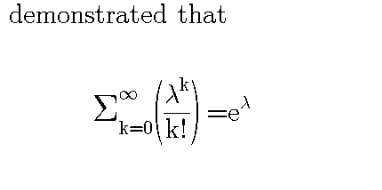
Answered by OlafThorendsen last updated on 13/Jul/20
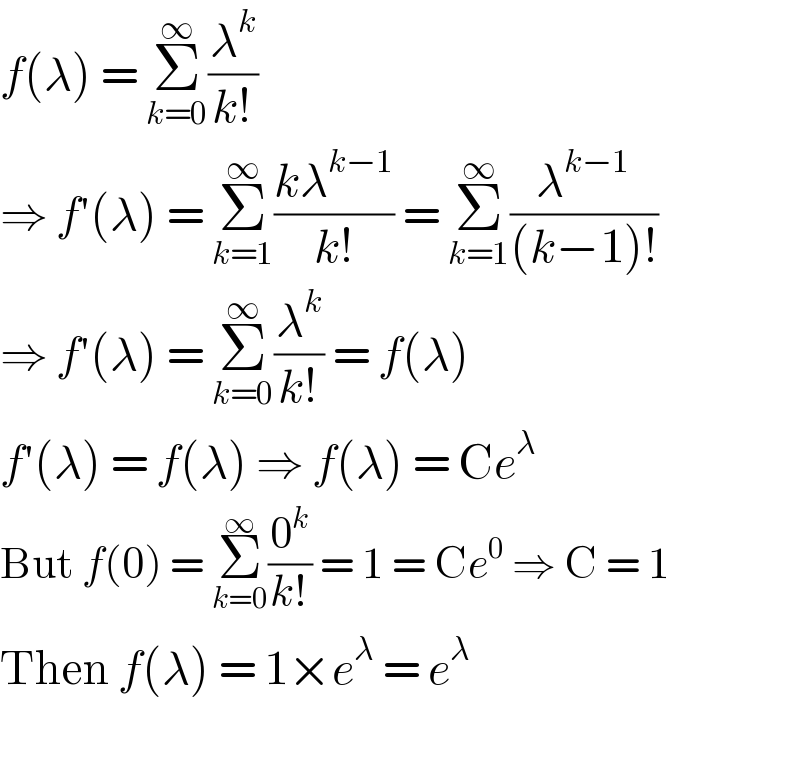
$${f}\left(\lambda\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\lambda^{{k}} }{{k}!} \\ $$$$\Rightarrow\:{f}'\left(\lambda\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}\lambda^{{k}−\mathrm{1}} }{{k}!}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\lambda^{{k}−\mathrm{1}} }{\left({k}−\mathrm{1}\right)!} \\ $$$$\Rightarrow\:{f}'\left(\lambda\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\lambda^{{k}} }{{k}!}\:=\:{f}\left(\lambda\right) \\ $$$${f}'\left(\lambda\right)\:=\:{f}\left(\lambda\right)\:\Rightarrow\:{f}\left(\lambda\right)\:=\:\mathrm{C}{e}^{\lambda} \\ $$$$\mathrm{But}\:{f}\left(\mathrm{0}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{0}^{{k}} }{{k}!}\:=\:\mathrm{1}\:=\:\mathrm{C}{e}^{\mathrm{0}} \:\Rightarrow\:\mathrm{C}\:=\:\mathrm{1} \\ $$$$\mathrm{Then}\:{f}\left(\lambda\right)\:=\:\mathrm{1}×{e}^{\lambda} \:=\:{e}^{\lambda} \\ $$$$ \\ $$
Answered by OlafThorendsen last updated on 13/Jul/20
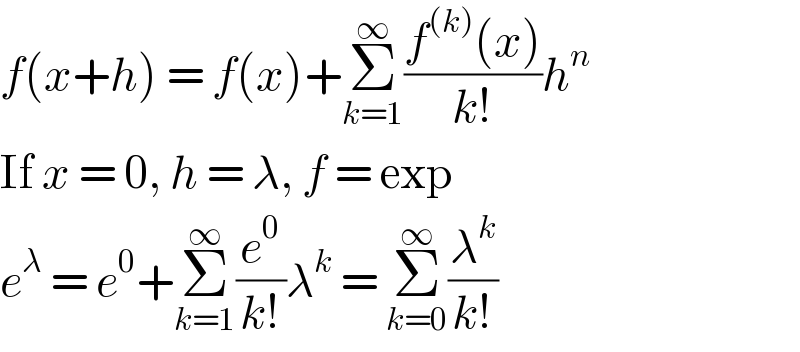
$${f}\left({x}+{h}\right)\:=\:{f}\left({x}\right)+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{f}^{\left({k}\right)} \left({x}\right)}{{k}!}{h}^{{n}} \\ $$$$\mathrm{If}\:{x}\:=\:\mathrm{0},\:{h}\:=\:\lambda,\:{f}\:=\:\mathrm{exp} \\ $$$${e}^{\lambda} \:=\:{e}^{\mathrm{0}} +\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{\mathrm{0}} }{{k}!}\lambda^{{k}} \:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\lambda^{{k}} }{{k}!} \\ $$
