
Question Number 10323 by amir last updated on 04/Feb/17

Answered by mrW1 last updated on 04/Feb/17
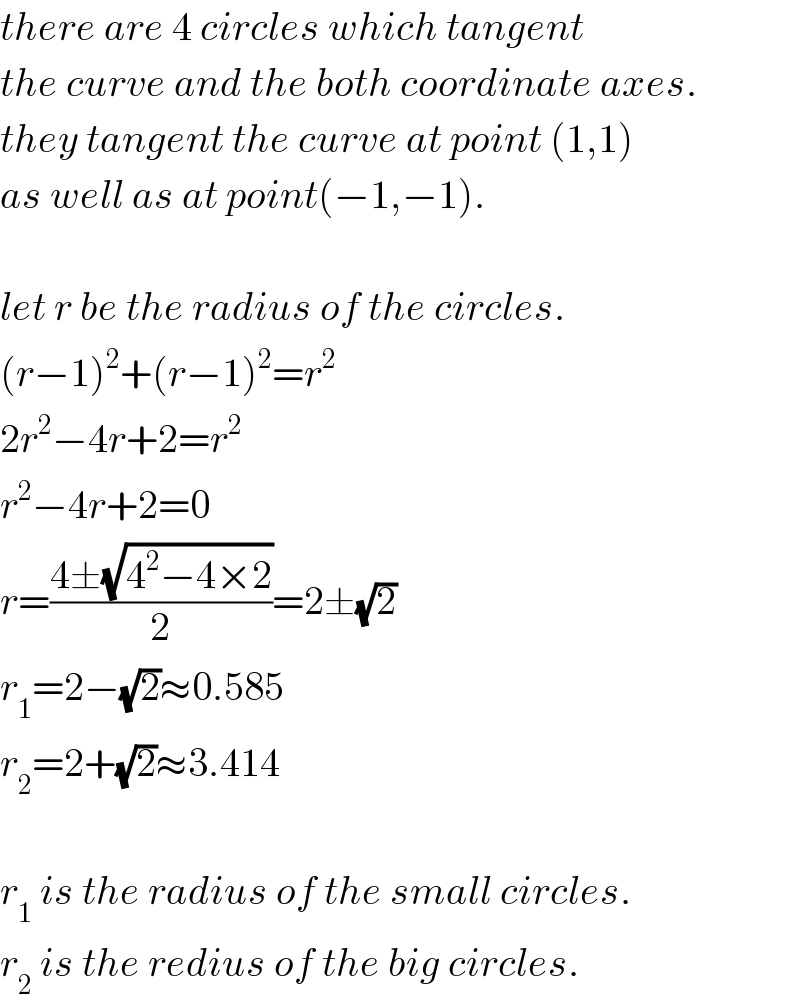
$${there}\:{are}\:\mathrm{4}\:{circles}\:{which}\:{tangent} \\ $$$${the}\:{curve}\:{and}\:{the}\:{both}\:{coordinate}\:{axes}. \\ $$$${they}\:{tangent}\:{the}\:{curve}\:{at}\:{point}\:\left(\mathrm{1},\mathrm{1}\right) \\ $$$${as}\:{well}\:{as}\:{at}\:{point}\left(−\mathrm{1},−\mathrm{1}\right). \\ $$$$ \\ $$$${let}\:{r}\:{be}\:{the}\:{radius}\:{of}\:{the}\:{circles}. \\ $$$$\left({r}−\mathrm{1}\right)^{\mathrm{2}} +\left({r}−\mathrm{1}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{2}{r}^{\mathrm{2}} −\mathrm{4}{r}+\mathrm{2}={r}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\mathrm{4}{r}+\mathrm{2}=\mathrm{0} \\ $$$${r}=\frac{\mathrm{4}\pm\sqrt{\mathrm{4}^{\mathrm{2}} −\mathrm{4}×\mathrm{2}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{2}} \\ $$$${r}_{\mathrm{1}} =\mathrm{2}−\sqrt{\mathrm{2}}\approx\mathrm{0}.\mathrm{585} \\ $$$${r}_{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{2}}\approx\mathrm{3}.\mathrm{414} \\ $$$$ \\ $$$${r}_{\mathrm{1}} \:{is}\:{the}\:{radius}\:{of}\:{the}\:{small}\:{circles}. \\ $$$${r}_{\mathrm{2}} \:{is}\:{the}\:{redius}\:{of}\:{the}\:{big}\:{circles}. \\ $$
Commented by mrW1 last updated on 04/Feb/17

Commented by amir last updated on 08/Feb/17

$${hello}\:{dear}\:{mrw}\mathrm{1}.{thank}\:{you}\:{very}\:{much} \\ $$$${I}\:{have}\:{another}\:{solotion}\:{for}\:{this}\:{Q}. \\ $$$${because}\:{of}\:{the}\:{circle}\:{tangent}\:{to}\:{the}\: \\ $$$${cordinate}\:{axes}\:,{the}\:{cordinates}\:{of}\: \\ $$$${its}\:{center}\:{are}\:{O}\begin{pmatrix}{{r}}\\{{r}}\end{pmatrix}\:\:{and}\:{its}\:{equation} \\ $$$${will}\:{be}\:\left({x}−{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}.} \\ $$$${by}\:{replacing}\:\:{y}=\frac{\mathrm{1}}{{x}}\:{in}\:{this}\:{equation} \\ $$$${we}\:{have}\:\:\:\left({x}−{r}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{x}}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left({x}−{r}\right)^{\mathrm{2}} +\left(\mathrm{1}−{rx}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} {x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} −\mathrm{2}{rx}^{\mathrm{3}} +{r}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{rx}+\mathrm{1}=\mathrm{0} \\ $$$${or} \\ $$$${x}^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{2}{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right){r}+\left(\mathrm{1}+{x}^{\mathrm{4}} \right)=\mathrm{0} \\ $$$${r}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}}=\frac{−\mathrm{2}{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\pm\sqrt{\mathrm{4}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{4}} \right)}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$${r}={x}+\frac{\mathrm{1}}{{x}}\pm\sqrt{\mathrm{2}} \\ $$$${p}=\mathrm{2}\pi{r}=\mathrm{2}\pi\left({x}+\frac{\mathrm{1}}{{x}}\pm\sqrt{\mathrm{2}}\right) \\ $$$$\frac{{dp}}{{dx}}=\mathrm{0}\: \\ $$$$\mathrm{2}\pi\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\:{x}=\mathrm{1}\:\:\:\:{x}=−\mathrm{1} \\ $$$${r}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}\pm\sqrt{\mathrm{2}=}\mathrm{2}\pm\sqrt{\mathrm{2}}\:\:\:\:\blacksquare \\ $$
Commented by mrW1 last updated on 04/Feb/17

$${you}\:{are}\:{basically}\:{right}.\:{I}\:{have}\:{cut} \\ $$$${short}\:{the}\:{calculation},\:{because}\:{we} \\ $$$${know}\:{due}\:{to}\:{symmetry}\:{that}\:{the} \\ $$$${circles}\:{tangent}\:{the}\:{curve}\:{at}\:\left(\mathrm{1},\mathrm{1}\right) \\ $$$${as}\:{well}\:{as}\:{at}\:\left(−\mathrm{1},−\mathrm{1}\right). \\ $$
