
Question Number 103286 by bemath last updated on 14/Jul/20
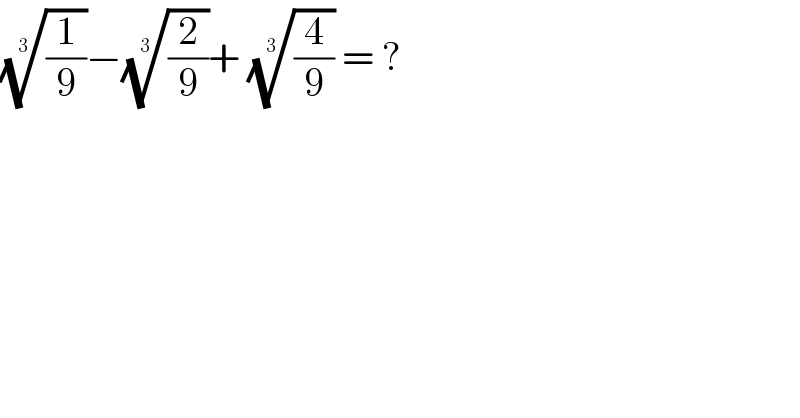
$$\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}}{\mathrm{9}}}+\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{4}}{\mathrm{9}}}\:=\:? \\ $$
Commented by bemath last updated on 14/Jul/20

$${yes}.\:{thank}\:{both} \\ $$
Answered by floor(10²Eta[1]) last updated on 14/Jul/20

$$\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}} \\ $$$$ \\ $$
Answered by OlafThorendsen last updated on 14/Jul/20
![x = ((1/9))^(1/3) −((2/9))^(1/3) + ((4/9))^(1/3) x = (1/3^(2/3) )(1−2^(1/3) +2^(2/3) ) x^3 = (1/9)(1−2^(1/3) +2^(2/3) )^3 (a+b+c)^3 = a^3 +b^3 +c^3 +3(a+b)(b+c)(c+a) a = 1, b = −2^(1/3) , c = 2^(2/3) x^3 = (1/9)[1−2+4+3(1−2^(1/3) )(−2^(1/3) +2^(2/3) )(2^(2/3) +1)] x^3 = (1/9)[3+3.2^(1/3) (1−2^(1/3) )(2^(1/3) −1)(2^(2/3) +1)] x^3 = (1/9)[3−3.2^(1/3) (2^(2/3) −2.2^(1/3) +1)(2^(2/3) +1)] x^3 = (1/3)[1+2^(1/3) (2^(4/3) −2^(2/3) −1)(2^(2/3) +1)] x^3 = (1/3)[1+(2^(5/3) −2−2^(1/3) )(2^(2/3) +1)] x^3 = (1/3)[1+(2^(7/3) −2^(5/3) −2+2^(5/3) −2−2^(1/3) )] x^3 = (1/3)[−3+2^(7/3) −2^(1/3) ] x^3 = (1/3)[−3+4.2^(1/3) −2^(1/3) ] x^3 = (1/3)[−3+3.2^(1/3) ] x^3 = 2^(1/3) −1 x = (((2)^(1/3) −1))^(1/3)](Q103291.png)
$${x}\:=\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}}{\mathrm{9}}}+\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{4}}{\mathrm{9}}} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}/\mathrm{3}} }\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}/\mathrm{3}} +\mathrm{2}^{\mathrm{2}/\mathrm{3}} \right) \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}/\mathrm{3}} +\mathrm{2}^{\mathrm{2}/\mathrm{3}} \right)^{\mathrm{3}} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{3}} \:=\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{3}\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right) \\ $$$${a}\:=\:\mathrm{1},\:{b}\:=\:−\mathrm{2}^{\mathrm{1}/\mathrm{3}} ,\:{c}\:=\:\mathrm{2}^{\mathrm{2}/\mathrm{3}} \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{1}−\mathrm{2}+\mathrm{4}+\mathrm{3}\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}/\mathrm{3}} \right)\left(−\mathrm{2}^{\mathrm{1}/\mathrm{3}} +\mathrm{2}^{\mathrm{2}/\mathrm{3}} \right)\left(\mathrm{2}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}\right)\right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{3}+\mathrm{3}.\mathrm{2}^{\mathrm{1}/\mathrm{3}} \left(\mathrm{1}−\mathrm{2}^{\mathrm{1}/\mathrm{3}} \right)\left(\mathrm{2}^{\mathrm{1}/\mathrm{3}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}\right)\right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{3}−\mathrm{3}.\mathrm{2}^{\mathrm{1}/\mathrm{3}} \left(\mathrm{2}^{\mathrm{2}/\mathrm{3}} −\mathrm{2}.\mathrm{2}^{\mathrm{1}/\mathrm{3}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}\right)\right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{1}+\mathrm{2}^{\mathrm{1}/\mathrm{3}} \left(\mathrm{2}^{\mathrm{4}/\mathrm{3}} −\mathrm{2}^{\mathrm{2}/\mathrm{3}} −\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}\right)\right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{1}+\left(\mathrm{2}^{\mathrm{5}/\mathrm{3}} −\mathrm{2}−\mathrm{2}^{\mathrm{1}/\mathrm{3}} \right)\left(\mathrm{2}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}\right)\right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{1}+\left(\mathrm{2}^{\mathrm{7}/\mathrm{3}} −\mathrm{2}^{\mathrm{5}/\mathrm{3}} −\mathrm{2}+\mathrm{2}^{\mathrm{5}/\mathrm{3}} −\mathrm{2}−\mathrm{2}^{\mathrm{1}/\mathrm{3}} \right)\right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[−\mathrm{3}+\mathrm{2}^{\mathrm{7}/\mathrm{3}} −\mathrm{2}^{\mathrm{1}/\mathrm{3}} \right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[−\mathrm{3}+\mathrm{4}.\mathrm{2}^{\mathrm{1}/\mathrm{3}} −\mathrm{2}^{\mathrm{1}/\mathrm{3}} \right] \\ $$$${x}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[−\mathrm{3}+\mathrm{3}.\mathrm{2}^{\mathrm{1}/\mathrm{3}} \right] \\ $$$${x}^{\mathrm{3}} \:=\:\mathrm{2}^{\mathrm{1}/\mathrm{3}} −\mathrm{1} \\ $$$${x}\:=\:\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}} \\ $$$$ \\ $$
Answered by bramlex last updated on 14/Jul/20
![consider : x^2 −xy+y^2 = ((x^3 +y^3 )/(x+y)) with x = ((2/3))^(1/3) , y=((1/3))^(1/3) ((4/9))^(1/3) −((2/9))^(1/3) +((1/3))^(1/3) = (1/(((2/3))^(1/3) +((1/3))^(1/3) )) = (1/(((1/3))^(1/3) ((2)^(1/3) +1))) = ((3)^(1/3) /((2)^(1/3) +1)) [ recall (x+y)^3 =x^3 +3x^2 y+3xy^2 +y^3 ] = ((3/(((2)^(1/3) +1)^3 )))^(1/3) = ((3/(3+3 (2)^(1/3) +3((2)^(1/3) )^2 )))^(1/3) = ((1/(1+(2)^(1/3) +((2)^(1/3) )^2 )))^(1/3) =((1/((((2−1)/((2)^(1/3) −1))))))^(1/3) = (( (2)^(1/3) −1))^(1/3)](Q103297.png)
$$\mathrm{consider}\::\:\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} \:=\:\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} }{\mathrm{x}+\mathrm{y}} \\ $$$$\mathrm{with}\:\mathrm{x}\:=\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}}{\mathrm{3}}}\:,\:\mathrm{y}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\sqrt[{\mathrm{3}}]{\frac{\mathrm{4}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}}{\mathrm{9}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{3}}}\:=\: \\ $$$$\frac{\mathrm{1}}{\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}}{\mathrm{3}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{3}}}}\:=\:\frac{\mathrm{1}}{\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{3}}}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\mathrm{1}\right)} \\ $$$$=\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\mathrm{1}}\:\left[\:\mathrm{recall}\right. \\ $$$$\left.\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{3}} =\mathrm{x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} \mathrm{y}+\mathrm{3xy}^{\mathrm{2}} +\mathrm{y}^{\mathrm{3}} \:\right] \\ $$$$=\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{3}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{3}} }}\:= \\ $$$$\sqrt[{\mathrm{3}}]{\frac{\mathrm{3}}{\mathrm{3}+\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)^{\mathrm{2}} }}\:=\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\left(\frac{\mathrm{2}−\mathrm{1}}{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\right)}}\:=\:\sqrt[{\mathrm{3}}]{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\: \\ $$$$ \\ $$
