Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 103318 by I want to learn more last updated on 14/Jul/20

Commented by som(math1967) last updated on 14/Jul/20

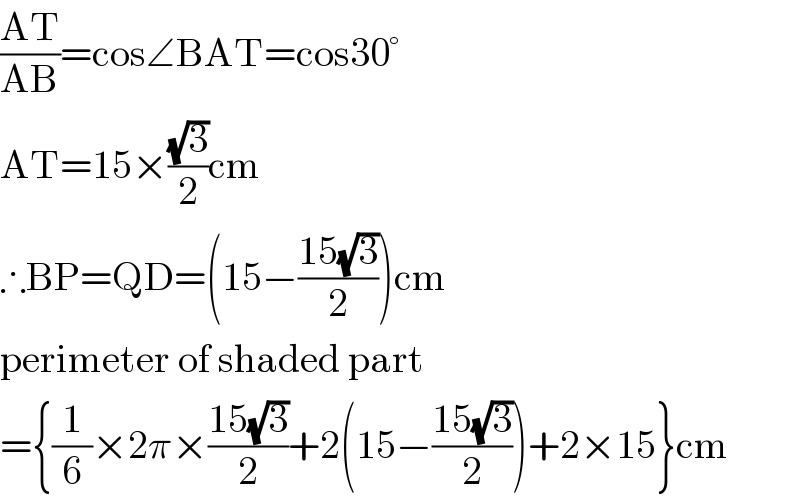
((AT)/(AB))=cos∠BAT=cos30° AT=15×((√3)/2)cm ∴BP=QD=(15−((15(√3))/2))cm perimeter of shaded part ={(1/6)×2π×((15(√3))/2)+2(15−((15(√3))/2))+2×15}cm

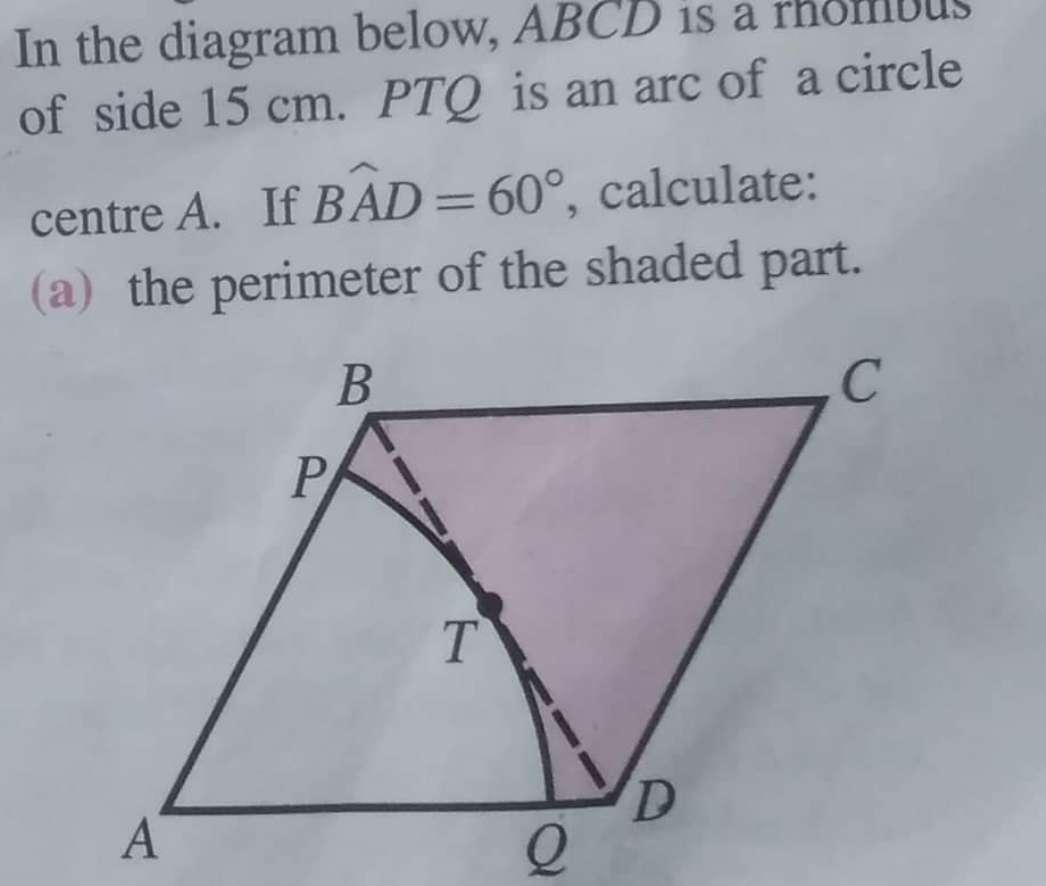
$$\frac{\mathrm{AT}}{\mathrm{AB}}=\mathrm{cos}\angle\mathrm{BAT}=\mathrm{cos30}° \\ $$$$\mathrm{AT}=\mathrm{15}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cm} \\ $$$$\therefore\mathrm{BP}=\mathrm{QD}=\left(\mathrm{15}−\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\mathrm{cm} \\ $$$$\mathrm{perimeter}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{part} \\ $$$$=\left\{\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{2}\pi×\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{2}\left(\mathrm{15}−\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\mathrm{2}×\mathrm{15}\right\}\mathrm{cm} \\ $$

Commented by I want to learn more last updated on 14/Jul/20

Thanks sir, i appreciate.

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$

Commented by Tawa11 last updated on 15/Sep/21

nice

$$\mathrm{nice} \\ $$

Answered by 1549442205 last updated on 14/Jul/20

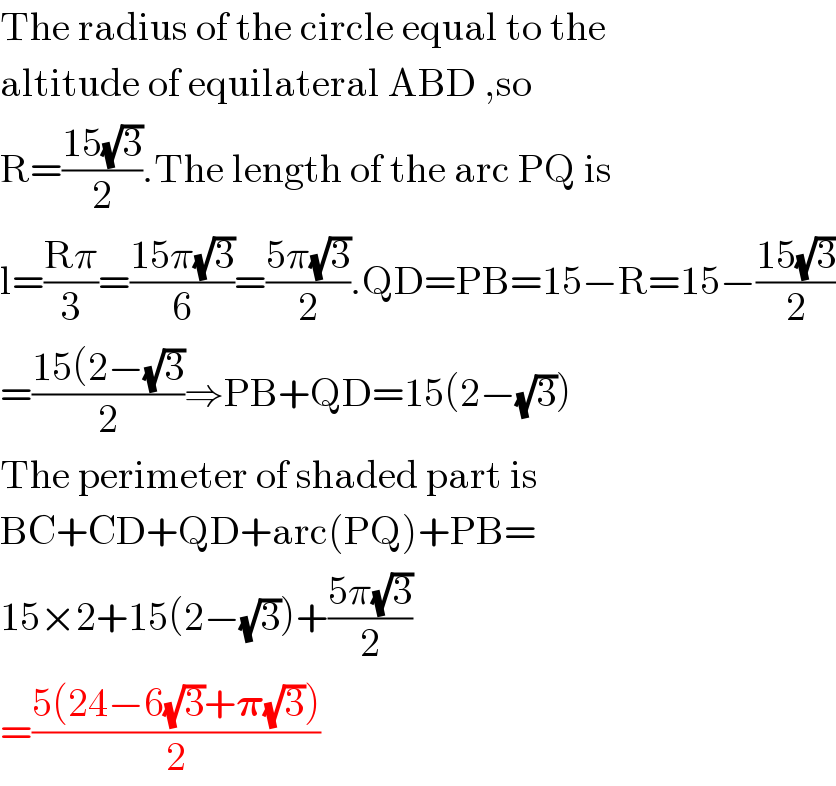
The radius of the circle equal to the altitude of equilateral ABD ,so R=((15(√3))/2).The length of the arc PQ is l=((Rπ)/3)=((15π(√3))/6)=((5π(√3))/2).QD=PB=15−R=15−((15(√3))/2) =((15(2−(√3))/2)⇒PB+QD=15(2−(√3)) The perimeter of shaded part is BC+CD+QD+arc(PQ)+PB= 15×2+15(2−(√3))+((5π(√3))/2) =((5(24−6(√3)+𝛑(√3)))/2)

$$\mathrm{The}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{altitude}\:\mathrm{of}\:\mathrm{equilateral}\:\mathrm{ABD}\:,\mathrm{so} \\ $$$$\mathrm{R}=\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}}.\mathrm{The}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{PQ}\:\mathrm{is} \\ $$$$\mathrm{l}=\frac{\mathrm{R}\pi}{\mathrm{3}}=\frac{\mathrm{15}\pi\sqrt{\mathrm{3}}}{\mathrm{6}}=\frac{\mathrm{5}\pi\sqrt{\mathrm{3}}}{\mathrm{2}}.\mathrm{QD}=\mathrm{PB}=\mathrm{15}−\mathrm{R}=\mathrm{15}−\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{15}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right.}{\mathrm{2}}\Rightarrow\mathrm{PB}+\mathrm{QD}=\mathrm{15}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$$\mathrm{The}\:\mathrm{perimeter}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{part}\:\mathrm{is} \\ $$$$\mathrm{BC}+\mathrm{CD}+\mathrm{QD}+\mathrm{arc}\left(\mathrm{PQ}\right)+\mathrm{PB}= \\ $$$$\mathrm{15}×\mathrm{2}+\mathrm{15}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)+\frac{\mathrm{5}\pi\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{5}\left(\mathrm{24}−\mathrm{6}\sqrt{\mathrm{3}}+\boldsymbol{\pi}\sqrt{\mathrm{3}}\right)}{\mathrm{2}} \\ $$

Commented by I want to learn more last updated on 14/Jul/20

Thanks sir, i appreciate.

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$

Commented by I want to learn more last updated on 14/Jul/20

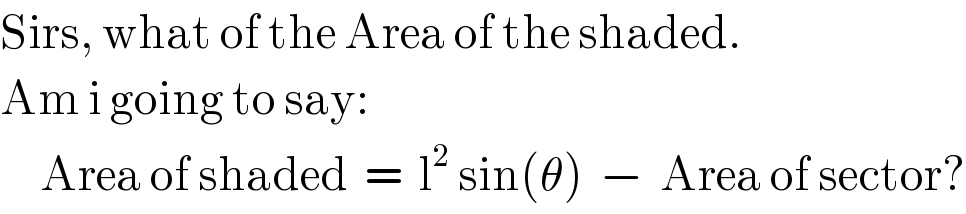
Sirs, what of the Area of the shaded. Am i going to say: Area of shaded = l^2 sin(θ) − Area of sector?

$$\mathrm{Sirs},\:\mathrm{what}\:\mathrm{of}\:\mathrm{the}\:\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shaded}. \\ $$$$\mathrm{Am}\:\mathrm{i}\:\mathrm{going}\:\mathrm{to}\:\mathrm{say}: \\ $$$$\:\:\:\:\:\mathrm{Area}\:\mathrm{of}\:\mathrm{shaded}\:\:=\:\:\mathrm{l}^{\mathrm{2}} \:\mathrm{sin}\left(\theta\right)\:\:−\:\:\mathrm{Area}\:\mathrm{of}\:\mathrm{sector}? \\ $$

Commented by som(math1967) last updated on 14/Jul/20

Area of rhombus−Area of sector

$$\mathrm{Area}\:\mathrm{of}\:\mathrm{rhombus}−\mathrm{Area}\:\mathrm{of} \\ $$$$\mathrm{sector} \\ $$

Commented by I want to learn more last updated on 14/Jul/20

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Commented by 1549442205 last updated on 14/Jul/20

The area of rhombs is S=((AC×BD)/2)=((15(√3)×15(√3))/4)=((675)/4) The area of the secror is S_0 =((πR^2 )/6)=(π/6)×(((15(√3))/2))^2 =((675π)/(24)) The area of shaded part is: S_(sh) =S−S_0 =((675)/4)−((675𝛑)/(24))=((675(6−𝛑))/(24))

$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{rhombs}\:\mathrm{is}\:\mathrm{S}=\frac{\mathrm{AC}×\mathrm{BD}}{\mathrm{2}}=\frac{\mathrm{15}\sqrt{\mathrm{3}}×\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{\mathrm{675}}{\mathrm{4}} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{secror}\:\mathrm{is}\:\:\mathrm{S}_{\mathrm{0}} =\frac{\pi\mathrm{R}^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi}{\mathrm{6}}×\left(\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{675}\pi}{\mathrm{24}} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{part}\:\mathrm{is}: \\ $$$$\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{sh}}} =\boldsymbol{\mathrm{S}}−\boldsymbol{\mathrm{S}}_{\mathrm{0}} =\frac{\mathrm{675}}{\mathrm{4}}−\frac{\mathrm{675}\boldsymbol{\pi}}{\mathrm{24}}=\frac{\mathrm{675}\left(\mathrm{6}−\boldsymbol{\pi}\right)}{\mathrm{24}} \\ $$$$ \\ $$

Commented by I want to learn more last updated on 14/Jul/20

Thanks sir. I apreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{apreciate}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com