Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 103321 by bemath last updated on 14/Jul/20

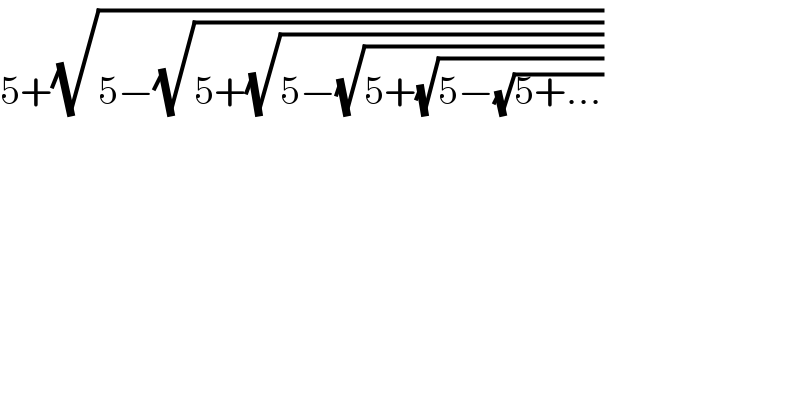
5+(√(5−(√(5+(√(5−(√(5+(√(5−(√(5+...))))))))))))

$$\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{\mathrm{5}+...}}}}}} \\ $$

Answered by Dwaipayan Shikari last updated on 14/Jul/20

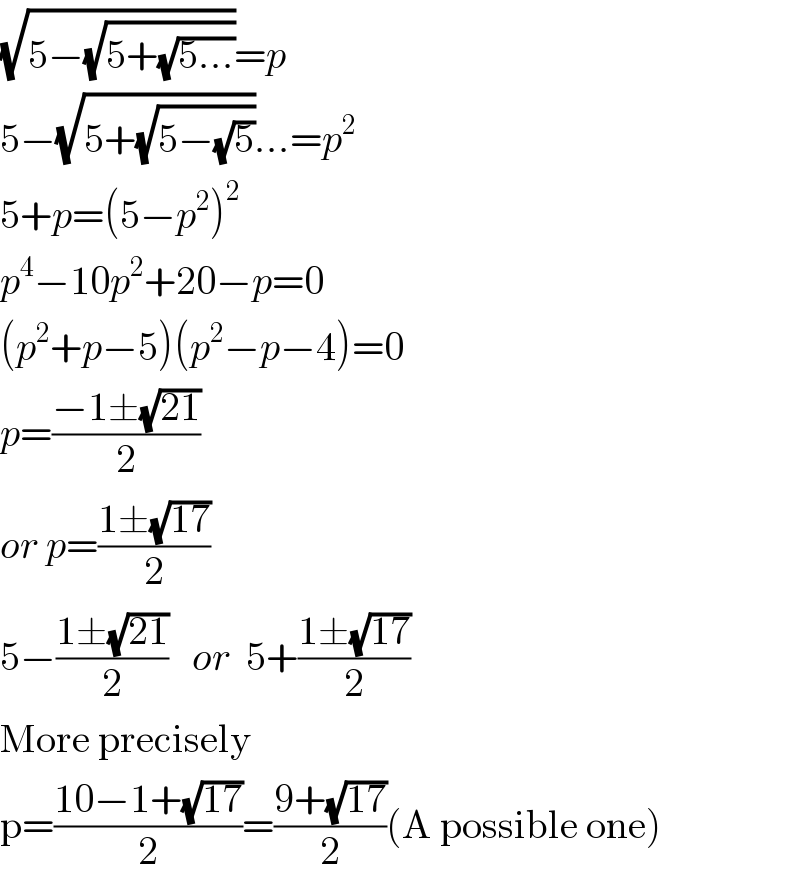
(√(5−(√(5+(√(5...))))))=p 5−(√(5+(√(5−(√5)))))...=p^2 5+p=(5−p^2 )^2 p^4 −10p^2 +20−p=0 (p^2 +p−5)(p^2 −p−4)=0 p=((−1±(√(21)))/2) or p=((1±(√(17)))/2) 5−((1±(√(21)))/2) or 5+((1±(√(17)))/2) More precisely p=((10−1+(√(17)))/2)=((9+(√(17)))/2)(A possible one)

$$\sqrt{\mathrm{5}−\sqrt{\mathrm{5}+\sqrt{\mathrm{5}...}}}={p} \\ $$$$\mathrm{5}−\sqrt{\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{\mathrm{5}}}}...={p}^{\mathrm{2}} \\ $$$$\mathrm{5}+{p}=\left(\mathrm{5}−{p}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${p}^{\mathrm{4}} −\mathrm{10}{p}^{\mathrm{2}} +\mathrm{20}−{p}=\mathrm{0} \\ $$$$\left({p}^{\mathrm{2}} +{p}−\mathrm{5}\right)\left({p}^{\mathrm{2}} −{p}−\mathrm{4}\right)=\mathrm{0} \\ $$$${p}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$${or}\:{p}=\frac{\mathrm{1}\pm\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\mathrm{5}−\frac{\mathrm{1}\pm\sqrt{\mathrm{21}}}{\mathrm{2}}\:\:\:{or}\:\:\mathrm{5}+\frac{\mathrm{1}\pm\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\mathrm{More}\:\mathrm{precisely} \\ $$$$\mathrm{p}=\frac{\mathrm{10}−\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}=\frac{\mathrm{9}+\sqrt{\mathrm{17}}}{\mathrm{2}}\left(\mathrm{A}\:\mathrm{possible}\:\mathrm{one}\right) \\ $$

Answered by OlafThorendsen last updated on 14/Jul/20

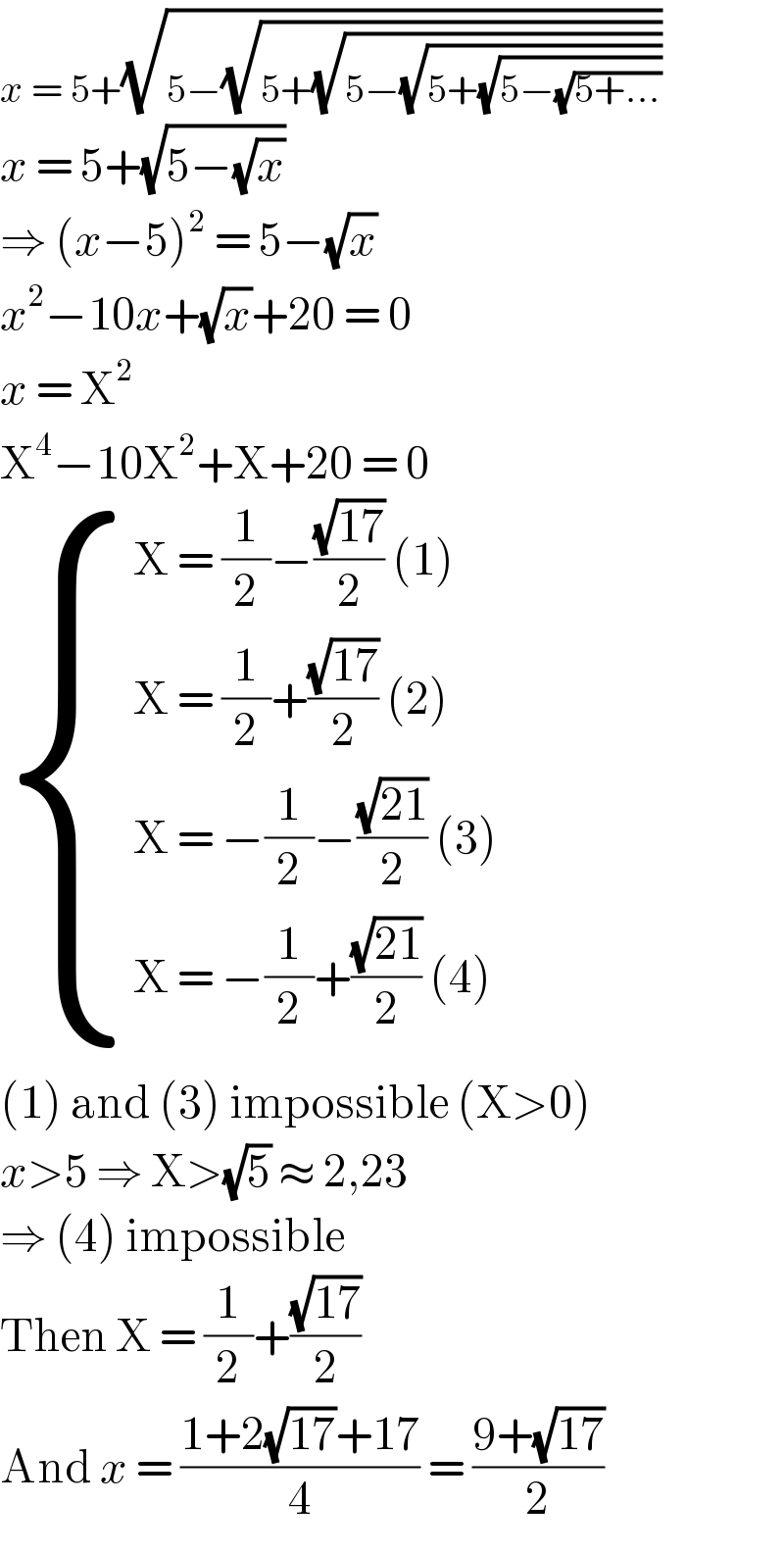
x = 5+(√(5−(√(5+(√(5−(√(5+(√(5−(√(5+...)))))))))))) x = 5+(√(5−(√x))) ⇒ (x−5)^2 = 5−(√x) x^2 −10x+(√x)+20 = 0 x = X^2 X^4 −10X^2 +X+20 = 0 { ((X = (1/2)−((√(17))/2) (1))),((X = (1/2)+((√(17))/2) (2))),((X = −(1/2)−((√(21))/2) (3))),((X = −(1/2)+((√(21))/2) (4))) :} (1) and (3) impossible (X>0) x>5 ⇒ X>(√5) ≈ 2,23 ⇒ (4) impossible Then X = (1/2)+((√(17))/2) And x = ((1+2(√(17))+17)/4) = ((9+(√(17)))/2)

$${x}\:=\:\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{\mathrm{5}+...}}}}}} \\ $$$${x}\:=\:\mathrm{5}+\sqrt{\mathrm{5}−\sqrt{{x}}} \\ $$$$\Rightarrow\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} \:=\:\mathrm{5}−\sqrt{{x}} \\ $$$${x}^{\mathrm{2}} −\mathrm{10}{x}+\sqrt{{x}}+\mathrm{20}\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{X}^{\mathrm{2}} \\ $$$$\mathrm{X}^{\mathrm{4}} −\mathrm{10X}^{\mathrm{2}} +\mathrm{X}+\mathrm{20}\:=\:\mathrm{0} \\ $$$$\begin{cases}{\mathrm{X}\:=\:\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{17}}}{\mathrm{2}}\:\left(\mathrm{1}\right)}\\{\mathrm{X}\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{17}}}{\mathrm{2}}\:\left(\mathrm{2}\right)}\\{\mathrm{X}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{21}}}{\mathrm{2}}\:\left(\mathrm{3}\right)}\\{\mathrm{X}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{21}}}{\mathrm{2}}\:\left(\mathrm{4}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{3}\right)\:\mathrm{impossible}\:\left(\mathrm{X}>\mathrm{0}\right) \\ $$$${x}>\mathrm{5}\:\Rightarrow\:\mathrm{X}>\sqrt{\mathrm{5}}\:\approx\:\mathrm{2},\mathrm{23} \\ $$$$\Rightarrow\:\left(\mathrm{4}\right)\:\mathrm{impossible} \\ $$$$\mathrm{Then}\:\mathrm{X}\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\mathrm{And}\:{x}\:=\:\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{17}}+\mathrm{17}}{\mathrm{4}}\:=\:\frac{\mathrm{9}+\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com