Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 103345 by harckinwunmy last updated on 14/Jul/20

Commented by harckinwunmy last updated on 14/Jul/20

please help

$$\mathrm{please}\:\mathrm{help} \\ $$

Commented by Dwaipayan Shikari last updated on 14/Jul/20

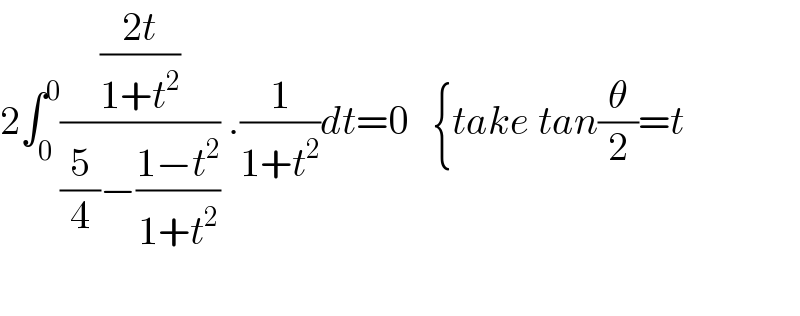
2∫_0 ^0 (((2t)/(1+t^2 ))/((5/4)−((1−t^2 )/(1+t^2 )))) .(1/(1+t^2 ))dt=0 {take tan(θ/2)=t

$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{0}} \frac{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\mathrm{0}\:\:\:\left\{{take}\:{tan}\frac{\theta}{\mathrm{2}}={t}\right. \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 14/Jul/20

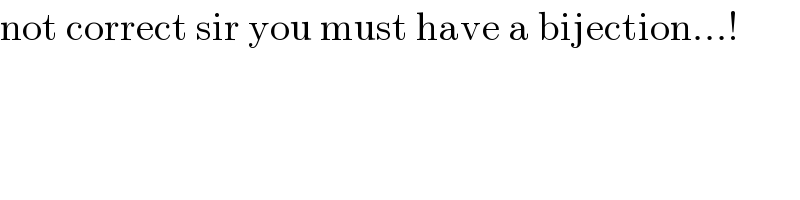
not correct sir you must have a bijection...!

$$\mathrm{not}\:\mathrm{correct}\:\mathrm{sir}\:\mathrm{you}\:\mathrm{must}\:\mathrm{have}\:\mathrm{a}\:\mathrm{bijection}...! \\ $$

Commented by Dwaipayan Shikari last updated on 14/Jul/20

∫_0 ^0 f(x)dx=0

$$\int_{\mathrm{0}} ^{\mathrm{0}} {f}\left({x}\right){dx}=\mathrm{0} \\ $$

Commented by mathmax by abdo last updated on 15/Jul/20

tan is bijective on ]−(π/2),(π/2)[ not [0,2π] be carefull

$$\left.\mathrm{tan}\:\mathrm{is}\:\mathrm{bijective}\:\mathrm{on}\:\right]−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\left[\:\mathrm{not}\:\left[\mathrm{0},\mathrm{2}\pi\right]\:\mathrm{be}\:\mathrm{carefull}\right. \\ $$

Answered by abdomathmax last updated on 14/Jul/20

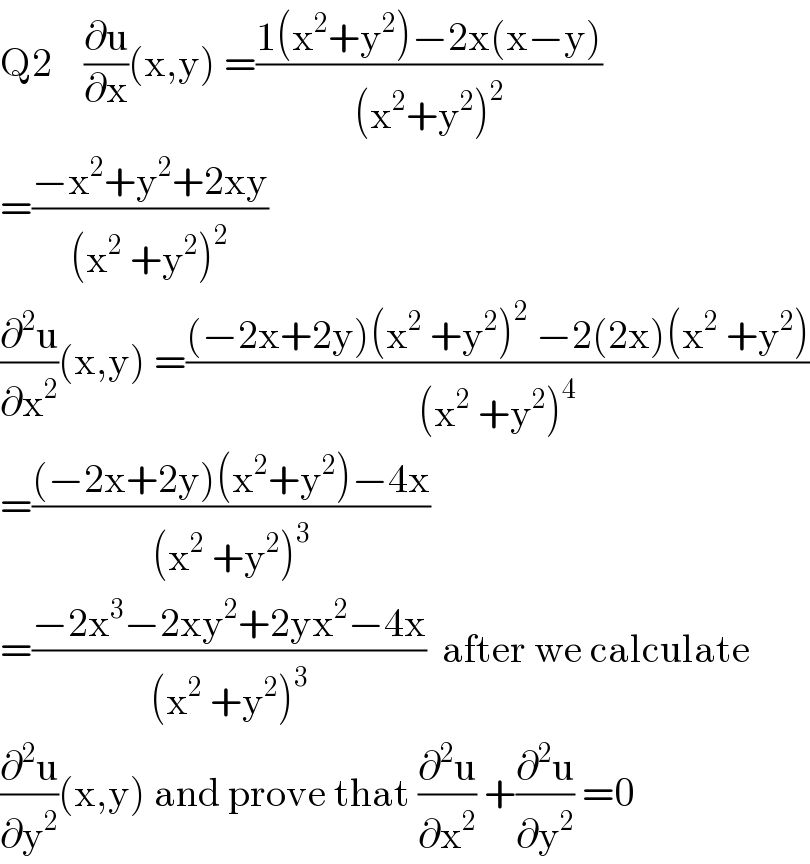
Q2 (∂u/∂x)(x,y) =((1(x^2 +y^2 )−2x(x−y))/((x^2 +y^2 )^2 )) =((−x^2 +y^2 +2xy)/((x^2 +y^2 )^2 )) (∂^2 u/∂x^2 )(x,y) =(((−2x+2y)(x^2 +y^2 )^2 −2(2x)(x^2 +y^2 ))/((x^2 +y^2 )^4 )) =(((−2x+2y)(x^2 +y^2 )−4x)/((x^2 +y^2 )^3 )) =((−2x^3 −2xy^2 +2yx^2 −4x)/((x^2 +y^2 )^3 )) after we calculate (∂^2 u/∂y^2 )(x,y) and prove that (∂^2 u/∂x^2 ) +(∂^2 u/∂y^2 ) =0

$$\mathrm{Q2}\:\:\:\:\frac{\partial\mathrm{u}}{\partial\mathrm{x}}\left(\mathrm{x},\mathrm{y}\right)\:=\frac{\mathrm{1}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)−\mathrm{2x}\left(\mathrm{x}−\mathrm{y}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{2xy}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\frac{\partial^{\mathrm{2}} \mathrm{u}}{\partial\mathrm{x}^{\mathrm{2}} }\left(\mathrm{x},\mathrm{y}\right)\:=\frac{\left(−\mathrm{2x}+\mathrm{2y}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{2}\left(\mathrm{2x}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$=\frac{\left(−\mathrm{2x}+\mathrm{2y}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)−\mathrm{4x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{2x}^{\mathrm{3}} −\mathrm{2xy}^{\mathrm{2}} +\mathrm{2yx}^{\mathrm{2}} −\mathrm{4x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{3}} }\:\:\mathrm{after}\:\mathrm{we}\:\mathrm{calculate} \\ $$$$\frac{\partial^{\mathrm{2}} \mathrm{u}}{\partial\mathrm{y}^{\mathrm{2}} }\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{and}\:\mathrm{prove}\:\mathrm{that}\:\frac{\partial^{\mathrm{2}} \mathrm{u}}{\partial\mathrm{x}^{\mathrm{2}} }\:+\frac{\partial^{\mathrm{2}} \mathrm{u}}{\partial\mathrm{y}^{\mathrm{2}} }\:=\mathrm{0} \\ $$

Answered by abdomathmax last updated on 14/Jul/20

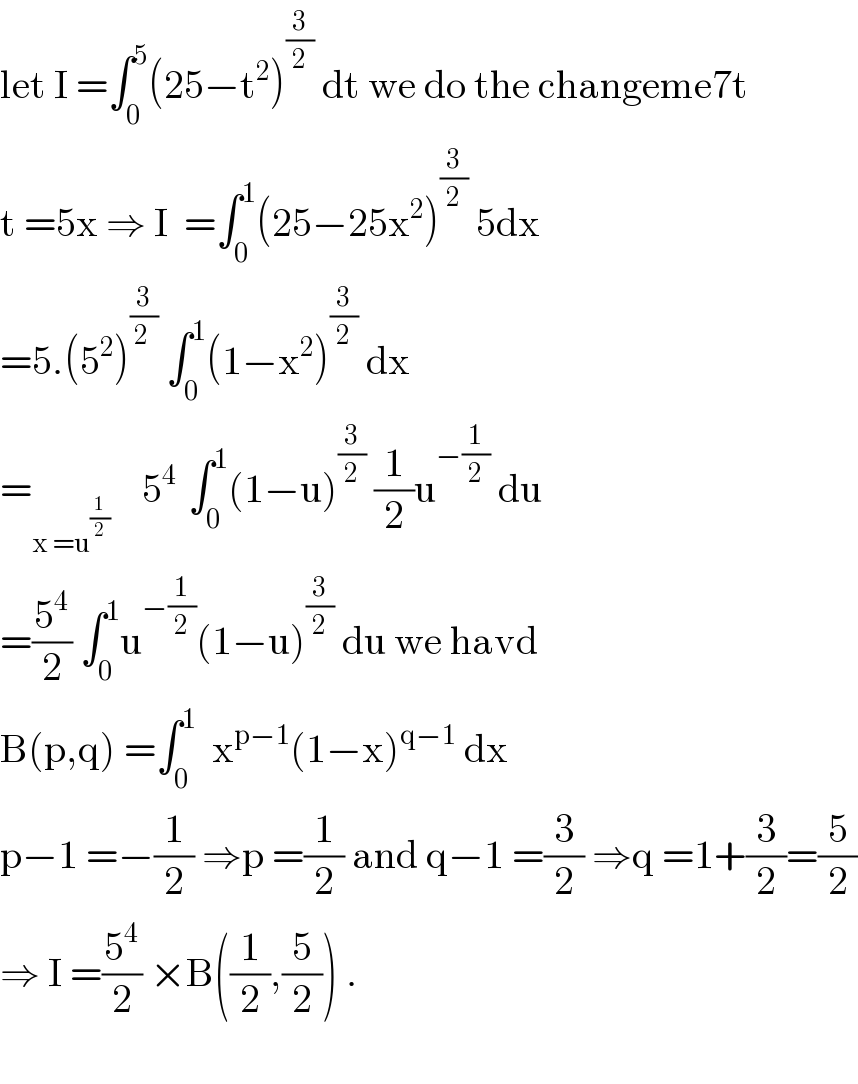
let I =∫_0 ^5 (25−t^2 )^(3/2) dt we do the changeme7t t =5x ⇒ I =∫_0 ^1 (25−25x^2 )^(3/2) 5dx =5.(5^2 )^(3/(2 )) ∫_0 ^1 (1−x^2 )^(3/2) dx =_(x =u^(1/2) ) 5^(4 ) ∫_0 ^1 (1−u)^(3/2) (1/2)u^(−(1/2)) du =(5^4 /2) ∫_0 ^1 u^(−(1/2)) (1−u)^(3/2) du we havd B(p,q) =∫_0 ^1 x^(p−1) (1−x)^(q−1) dx p−1 =−(1/2) ⇒p =(1/2) and q−1 =(3/2) ⇒q =1+(3/2)=(5/2) ⇒ I =(5^4 /2) ×B((1/2),(5/2)) .

$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{5}} \left(\mathrm{25}−\mathrm{t}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dt}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changeme7t} \\ $$$$\mathrm{t}\:=\mathrm{5x}\:\Rightarrow\:\mathrm{I}\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{25}−\mathrm{25x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{5dx} \\ $$$$=\mathrm{5}.\left(\mathrm{5}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}\:}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dx}\: \\ $$$$=_{\mathrm{x}\:=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} } \:\:\:\:\mathrm{5}^{\mathrm{4}\:} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{du} \\ $$$$=\frac{\mathrm{5}^{\mathrm{4}} }{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{du}\:\mathrm{we}\:\mathrm{havd} \\ $$$$\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\mathrm{x}^{\mathrm{p}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{q}−\mathrm{1}} \:\mathrm{dx} \\ $$$$\mathrm{p}−\mathrm{1}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{p}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{q}−\mathrm{1}\:=\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\mathrm{q}\:=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{5}^{\mathrm{4}} }{\mathrm{2}}\:×\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{2}}\right)\:. \\ $$$$ \\ $$

Answered by abdomathmax last updated on 14/Jul/20

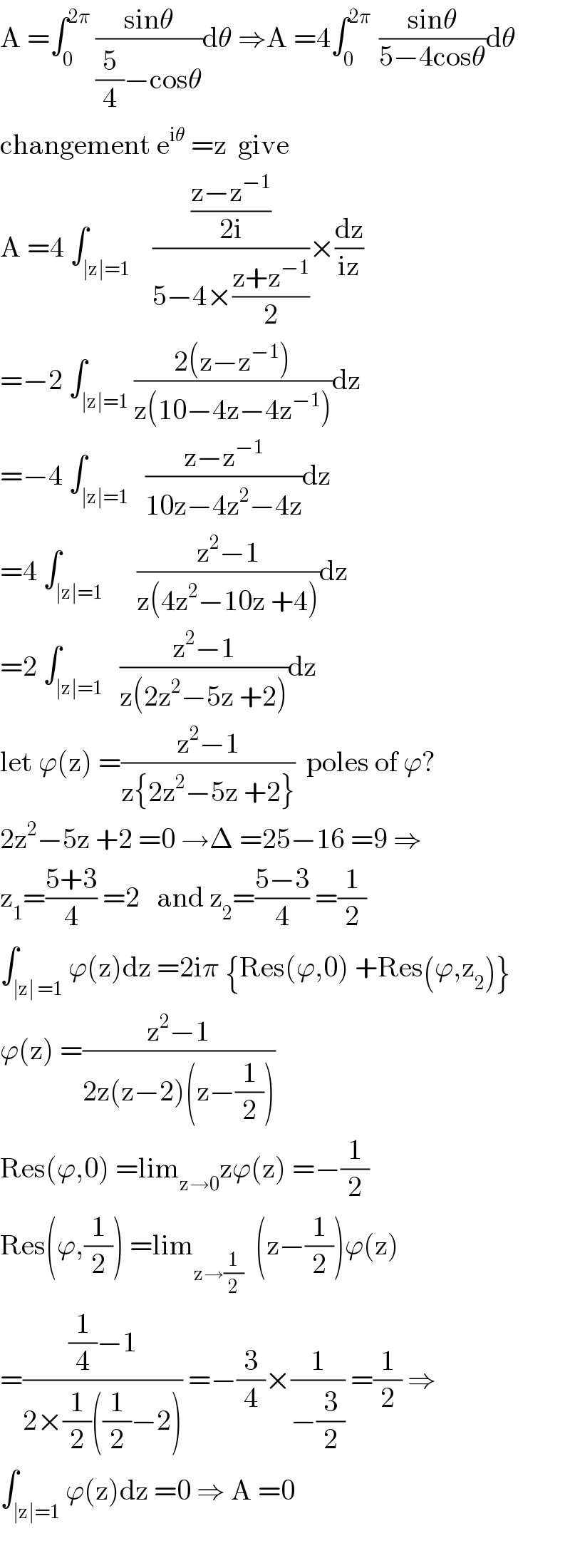
A =∫_0 ^(2π) ((sinθ)/((5/4)−cosθ))dθ ⇒A =4∫_0 ^(2π ) ((sinθ)/(5−4cosθ))dθ changement e^(iθ) =z give A =4 ∫_(∣z∣=1) (((z−z^(−1) )/(2i))/(5−4×((z+z^(−1) )/2)))×(dz/(iz)) =−2 ∫_(∣z∣=1) ((2(z−z^(−1) ))/(z(10−4z−4z^(−1) )))dz =−4 ∫_(∣z∣=1) ((z−z^(−1) )/(10z−4z^2 −4z))dz =4 ∫_(∣z∣=1) ((z^2 −1)/(z(4z^2 −10z +4)))dz =2 ∫_(∣z∣=1) ((z^2 −1)/(z(2z^2 −5z +2)))dz let ϕ(z) =((z^2 −1)/(z{2z^2 −5z +2})) poles of ϕ? 2z^2 −5z +2 =0 →Δ =25−16 =9 ⇒ z_1 =((5+3)/4) =2 and z_2 =((5−3)/4) =(1/2) ∫_(∣z∣ =1) ϕ(z)dz =2iπ {Res(ϕ,0) +Res(ϕ,z_2 )} ϕ(z) =((z^2 −1)/(2z(z−2)(z−(1/2)))) Res(ϕ,0) =lim_(z→0) zϕ(z) =−(1/2) Res(ϕ,(1/2)) =lim_(z→(1/2)) (z−(1/2))ϕ(z) =(((1/4)−1)/(2×(1/2)((1/2)−2))) =−(3/4)×(1/(−(3/2))) =(1/2) ⇒ ∫_(∣z∣=1) ϕ(z)dz =0 ⇒ A =0

$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{sin}\theta}{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{cos}\theta}\mathrm{d}\theta\:\Rightarrow\mathrm{A}\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{2}\pi\:} \:\frac{\mathrm{sin}\theta}{\mathrm{5}−\mathrm{4cos}\theta}\mathrm{d}\theta \\ $$$$\mathrm{changement}\:\mathrm{e}^{\mathrm{i}\theta} \:=\mathrm{z}\:\:\mathrm{give} \\ $$$$\mathrm{A}\:=\mathrm{4}\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2i}}}{\mathrm{5}−\mathrm{4}×\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}}×\frac{\mathrm{dz}}{\mathrm{iz}} \\ $$$$=−\mathrm{2}\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \frac{\mathrm{2}\left(\mathrm{z}−\mathrm{z}^{−\mathrm{1}} \right)}{\mathrm{z}\left(\mathrm{10}−\mathrm{4z}−\mathrm{4z}^{−\mathrm{1}} \right)}\mathrm{dz} \\ $$$$=−\mathrm{4}\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{10z}−\mathrm{4z}^{\mathrm{2}} −\mathrm{4z}}\mathrm{dz} \\ $$$$=\mathrm{4}\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{z}\left(\mathrm{4z}^{\mathrm{2}} −\mathrm{10z}\:+\mathrm{4}\right)}\mathrm{dz} \\ $$$$=\mathrm{2}\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{z}\left(\mathrm{2z}^{\mathrm{2}} −\mathrm{5z}\:+\mathrm{2}\right)}\mathrm{dz} \\ $$$$\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{z}\left\{\mathrm{2z}^{\mathrm{2}} −\mathrm{5z}\:+\mathrm{2}\right\}}\:\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{2z}^{\mathrm{2}} −\mathrm{5z}\:+\mathrm{2}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{25}−\mathrm{16}\:=\mathrm{9}\:\Rightarrow \\ $$$$\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{3}}{\mathrm{4}}\:=\mathrm{2}\:\:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{3}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\int_{\mid\mathrm{z}\mid\:=\mathrm{1}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\left\{\mathrm{Res}\left(\varphi,\mathrm{0}\right)\:+\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{2}} \right)\right\} \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2z}\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{0}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \mathrm{z}\varphi\left(\mathrm{z}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{Res}\left(\varphi,\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\frac{\mathrm{1}}{\mathrm{2}}} \:\:\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)\varphi\left(\mathrm{z}\right) \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}}{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)}\:=−\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{1}}{−\frac{\mathrm{3}}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{0}\:\Rightarrow\:\mathrm{A}\:=\mathrm{0} \\ $$$$ \\ $$

Answered by 1549442205 last updated on 15/Jul/20

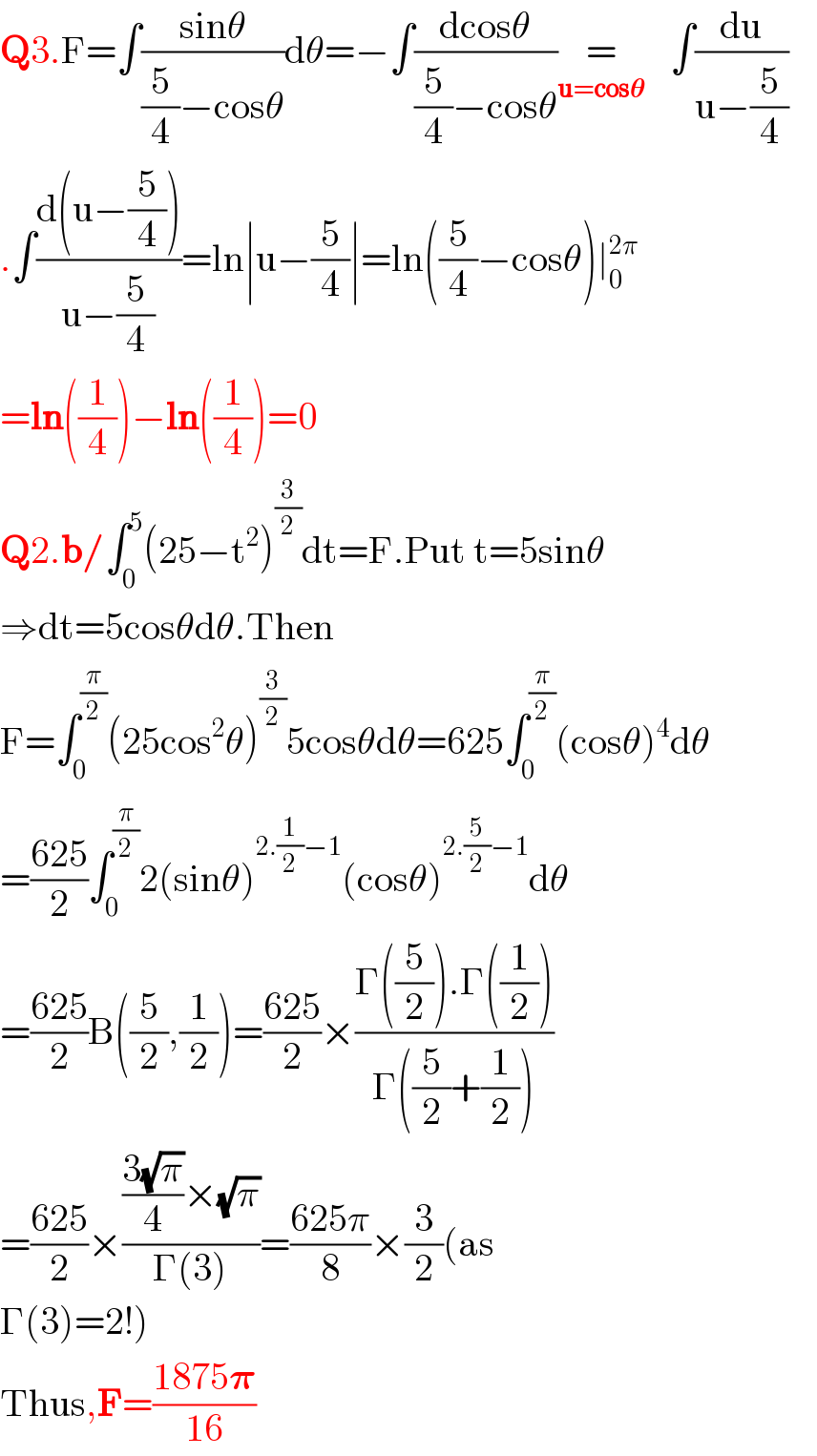
Q3.F=∫((sinθ)/((5/4)−cosθ))dθ=−∫((dcosθ)/((5/4)−cosθ))=_(u=cos𝛉) ∫(du/(u−(5/4))) .∫((d(u−(5/4)))/(u−(5/4)))=ln∣u−(5/4)∣=ln((5/4)−cosθ)∣_0 ^(2π) =ln((1/4))−ln((1/4))=0 Q2.b/∫_0 ^5 (25−t^2 )^(3/2) dt=F.Put t=5sinθ ⇒dt=5cosθdθ.Then F=∫_0 ^(π/2) (25cos^2 θ)^(3/2) 5cosθdθ=625∫_0 ^(π/2) (cosθ)^4 dθ =((625)/2)∫_0 ^(π/2) 2(sinθ)^(2.(1/2)−1) (cosθ)^(2.(5/2)−1) dθ =((625)/2)B((5/2),(1/2))=((625)/2)×((Γ((5/2)).Γ((1/2)))/(Γ((5/2)+(1/2)))) =((625)/2)×((((3(√π))/4)×(√π))/(Γ(3)))=((625π)/8)×(3/2)(as Γ(3)=2!) Thus,F=((1875𝛑)/(16))

$$\boldsymbol{\mathrm{Q}}\mathrm{3}.\mathrm{F}=\int\frac{\mathrm{sin}\theta}{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{cos}\theta}\mathrm{d}\theta=−\int\frac{\mathrm{dcos}\theta}{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{cos}\theta}\underset{\boldsymbol{\mathrm{u}}=\boldsymbol{\mathrm{cos}\theta}} {=}\:\:\:\:\:\:\:\int\frac{\mathrm{du}}{\mathrm{u}−\frac{\mathrm{5}}{\mathrm{4}}} \\ $$$$.\int\frac{\mathrm{d}\left(\mathrm{u}−\frac{\mathrm{5}}{\mathrm{4}}\right)}{\mathrm{u}−\frac{\mathrm{5}}{\mathrm{4}}}=\mathrm{ln}\mid\mathrm{u}−\frac{\mathrm{5}}{\mathrm{4}}\mid=\mathrm{ln}\left(\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{cos}\theta\right)\mid_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$=\boldsymbol{\mathrm{ln}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\boldsymbol{\mathrm{ln}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{Q}}\mathrm{2}.\boldsymbol{\mathrm{b}}/\int_{\mathrm{0}} ^{\mathrm{5}} \left(\mathrm{25}−\mathrm{t}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{dt}=\mathrm{F}.\mathrm{Put}\:\mathrm{t}=\mathrm{5sin}\theta \\ $$$$\Rightarrow\mathrm{dt}=\mathrm{5cos}\theta\mathrm{d}\theta.\mathrm{Then}\: \\ $$$$\mathrm{F}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{25cos}^{\mathrm{2}} \theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{5cos}\theta\mathrm{d}\theta=\mathrm{625}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cos}\theta\right)^{\mathrm{4}} \mathrm{d}\theta \\ $$$$=\frac{\mathrm{625}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{2}\left(\mathrm{sin}\theta\right)^{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{cos}\theta\right)^{\mathrm{2}.\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{1}} \mathrm{d}\theta \\ $$$$=\frac{\mathrm{625}}{\mathrm{2}}\mathrm{B}\left(\frac{\mathrm{5}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{625}}{\mathrm{2}}×\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{625}}{\mathrm{2}}×\frac{\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}×\sqrt{\pi}}{\Gamma\left(\mathrm{3}\right)}=\frac{\mathrm{625}\pi}{\mathrm{8}}×\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{as}\right. \\ $$$$\left.\Gamma\left(\mathrm{3}\right)=\mathrm{2}!\right) \\ $$$$\mathrm{Thus},\boldsymbol{\mathrm{F}}=\frac{\mathrm{1875}\boldsymbol{\pi}}{\mathrm{16}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com