Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 103389 by  M±th+et+s last updated on 14/Jul/20

Commented by  M±th+et+s last updated on 14/Jul/20

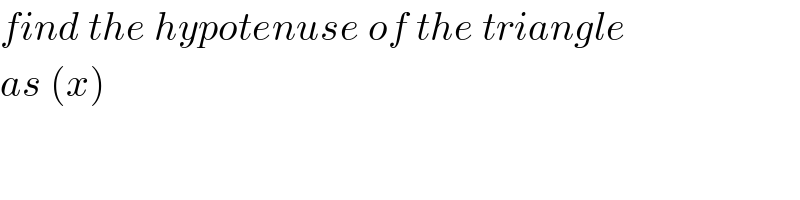
find the hypotenuse of the triangle as (x)

$${find}\:{the}\:{hypotenuse}\:{of}\:{the}\:{triangle} \\ $$$${as}\:\left({x}\right) \\ $$

Answered by OlafThorendsen last updated on 14/Jul/20

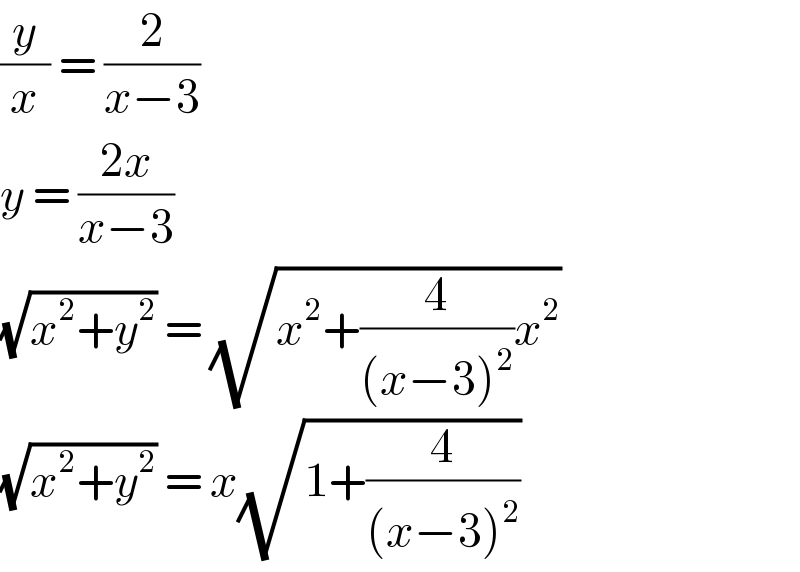
(y/x) = (2/(x−3)) y = ((2x)/(x−3)) (√(x^2 +y^2 )) = (√(x^2 +(4/((x−3)^2 ))x^2 )) (√(x^2 +y^2 )) = x(√(1+(4/((x−3)^2 ))))

$$\frac{{y}}{{x}}\:=\:\frac{\mathrm{2}}{{x}−\mathrm{3}} \\ $$$${y}\:=\:\frac{\mathrm{2}{x}}{{x}−\mathrm{3}} \\ $$$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\:\sqrt{{x}^{\mathrm{2}} +\frac{\mathrm{4}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }{x}^{\mathrm{2}} } \\ $$$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\:{x}\sqrt{\mathrm{1}+\frac{\mathrm{4}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }} \\ $$

Answered by bramlex last updated on 15/Jul/20

Commented by bramlex last updated on 15/Jul/20

((x−3)/3) = (2/(y−2)) ⇒((y−2)/2) = (3/(x−3)) y = (6/(x−3)) + 2 = ((6+2x−6)/(x−3)) y= ((2x)/(x−3)). hypotenusa r = (√(x^2 +y^2 )) r = (√(x^2 +(((2x)/(x−3)))^2 )) r= (√((x^2 (x−3)^2 +4x^2 )/((x−3)^2 ))) r = (x/(x−3)).(√(4+x^2 −6x+9)) r = (x/(x−3)).(√(x^2 −6+13)) ■

$$\frac{\mathrm{x}−\mathrm{3}}{\mathrm{3}}\:=\:\frac{\mathrm{2}}{\mathrm{y}−\mathrm{2}}\:\Rightarrow\frac{\mathrm{y}−\mathrm{2}}{\mathrm{2}}\:=\:\frac{\mathrm{3}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{6}}{\mathrm{x}−\mathrm{3}}\:+\:\mathrm{2}\:=\:\frac{\mathrm{6}+\mathrm{2x}−\mathrm{6}}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{y}=\:\frac{\mathrm{2x}}{\mathrm{x}−\mathrm{3}}.\: \\ $$$$\mathrm{hypotenusa}\:\mathrm{r}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \\ $$$$\mathrm{r}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\left(\frac{\mathrm{2x}}{\mathrm{x}−\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{r}=\:\sqrt{\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4x}^{\mathrm{2}} }{\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{r}\:=\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{3}}.\sqrt{\mathrm{4}+\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}} \\ $$$$\mathrm{r}\:=\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{3}}.\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{6}+\mathrm{13}}\:\blacksquare \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com