Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 103463 by bemath last updated on 15/Jul/20

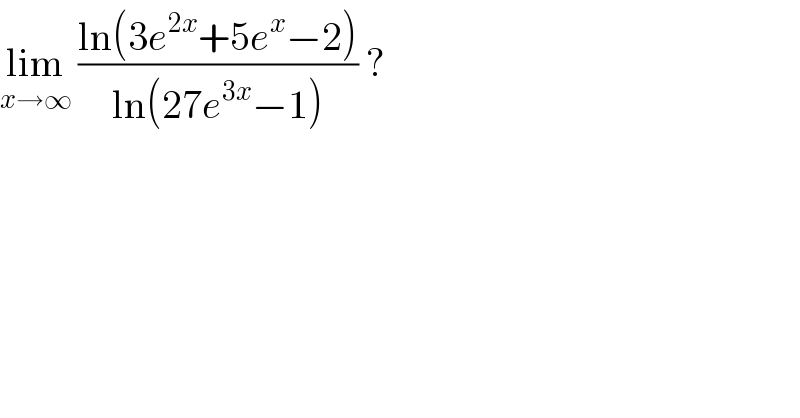
lim_(x→∞) ((ln(3e^(2x) +5e^x −2))/(ln(27e^(3x) −1))) ?

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{3}{e}^{\mathrm{2}{x}} +\mathrm{5}{e}^{{x}} −\mathrm{2}\right)}{\mathrm{ln}\left(\mathrm{27}{e}^{\mathrm{3}{x}} −\mathrm{1}\right)}\:? \\ $$

Answered by Worm_Tail last updated on 15/Jul/20

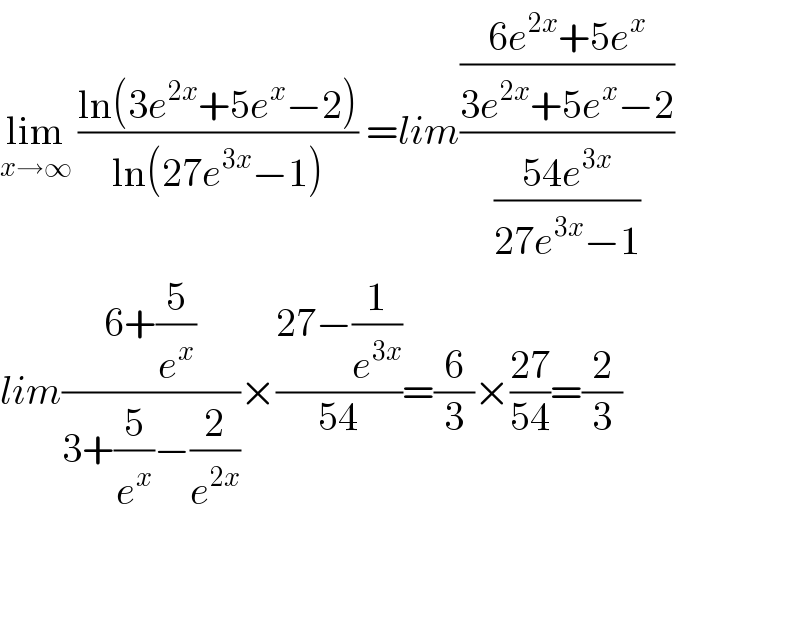
lim_(x→∞) ((ln(3e^(2x) +5e^x −2))/(ln(27e^(3x) −1))) =lim(((6e^(2x) +5e^x )/(3e^(2x) +5e^x −2))/((54e^(3x) )/(27e^(3x) −1))) lim((6+(5/e^x ))/(3+(5/e^x )−(2/e^(2x) )))×((27−(1/e^(3x) ))/(54))=(6/3)×((27)/(54))=(2/3)

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{3}{e}^{\mathrm{2}{x}} +\mathrm{5}{e}^{{x}} −\mathrm{2}\right)}{\mathrm{ln}\left(\mathrm{27}{e}^{\mathrm{3}{x}} −\mathrm{1}\right)}\:={lim}\frac{\frac{\mathrm{6}{e}^{\mathrm{2}{x}} +\mathrm{5}{e}^{{x}} }{\mathrm{3}{e}^{\mathrm{2}{x}} +\mathrm{5}{e}^{{x}} −\mathrm{2}}}{\frac{\mathrm{54}{e}^{\mathrm{3}{x}} }{\mathrm{27}{e}^{\mathrm{3}{x}} −\mathrm{1}}} \\ $$$${lim}\frac{\mathrm{6}+\frac{\mathrm{5}}{{e}^{{x}} }}{\mathrm{3}+\frac{\mathrm{5}}{{e}^{{x}} }−\frac{\mathrm{2}}{{e}^{\mathrm{2}{x}} }}×\frac{\mathrm{27}−\frac{\mathrm{1}}{{e}^{\mathrm{3}{x}} }}{\mathrm{54}}=\frac{\mathrm{6}}{\mathrm{3}}×\frac{\mathrm{27}}{\mathrm{54}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$

Answered by bobhans last updated on 15/Jul/20

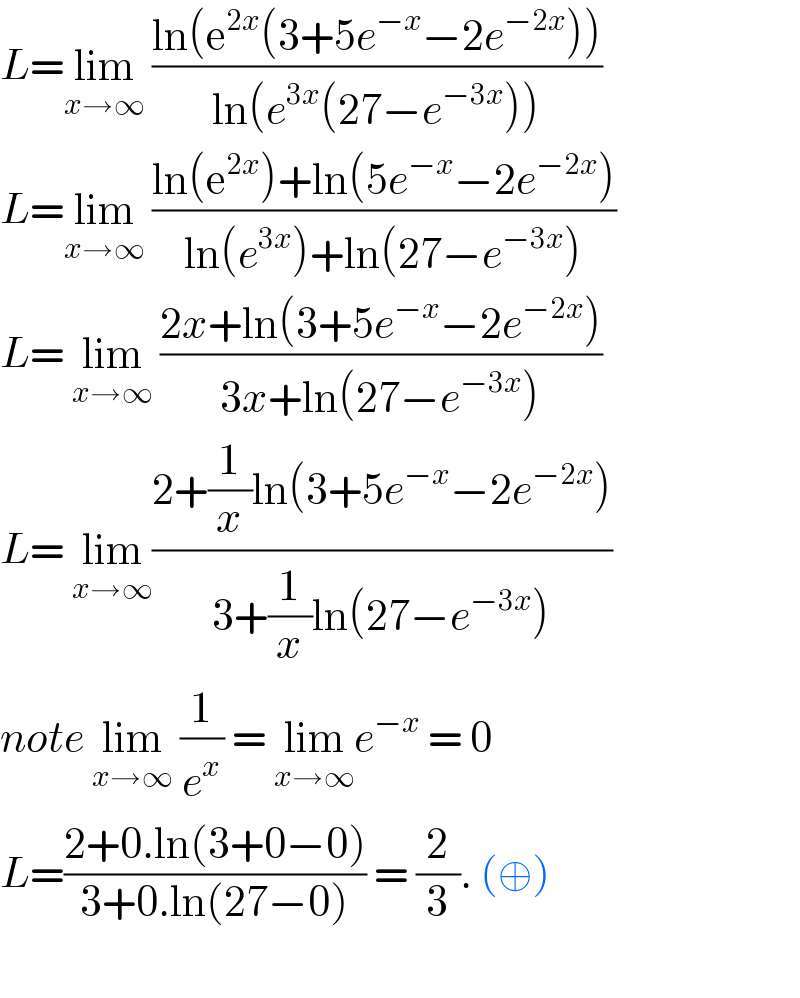
L=lim_(x→∞) ((ln(e^(2x) (3+5e^(−x) −2e^(−2x) )))/(ln(e^(3x) (27−e^(−3x) )))) L=lim_(x→∞) ((ln(e^(2x) )+ln(5e^(−x) −2e^(−2x) ))/(ln(e^(3x) )+ln(27−e^(−3x) ))) L= lim_(x→∞) ((2x+ln(3+5e^(−x) −2e^(−2x) ))/(3x+ln(27−e^(−3x) ))) L= lim_(x→∞) ((2+(1/x)ln(3+5e^(−x) −2e^(−2x) ))/(3+(1/x)ln(27−e^(−3x) ))) note lim_(x→∞) (1/e^x ) = lim_(x→∞) e^(−x) = 0 L=((2+0.ln(3+0−0))/(3+0.ln(27−0))) = (2/3). (⊕)

$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{e}^{\mathrm{2}{x}} \left(\mathrm{3}+\mathrm{5}{e}^{−{x}} −\mathrm{2}{e}^{−\mathrm{2}{x}} \right)\right)}{\mathrm{ln}\left({e}^{\mathrm{3}{x}} \left(\mathrm{27}−{e}^{−\mathrm{3}{x}} \right)\right)} \\ $$$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{e}^{\mathrm{2}{x}} \right)+\mathrm{ln}\left(\mathrm{5}{e}^{−{x}} −\mathrm{2}{e}^{−\mathrm{2}{x}} \right)}{\mathrm{ln}\left({e}^{\mathrm{3}{x}} \right)+\mathrm{ln}\left(\mathrm{27}−{e}^{−\mathrm{3}{x}} \right)} \\ $$$${L}=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2}{x}+\mathrm{ln}\left(\mathrm{3}+\mathrm{5}{e}^{−{x}} −\mathrm{2}{e}^{−\mathrm{2}{x}} \right)}{\mathrm{3}{x}+\mathrm{ln}\left(\mathrm{27}−{e}^{−\mathrm{3}{x}} \right)} \\ $$$${L}=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}+\frac{\mathrm{1}}{{x}}\mathrm{ln}\left(\mathrm{3}+\mathrm{5}{e}^{−{x}} −\mathrm{2}{e}^{−\mathrm{2}{x}} \right)}{\mathrm{3}+\frac{\mathrm{1}}{{x}}\mathrm{ln}\left(\mathrm{27}−{e}^{−\mathrm{3}{x}} \right)} \\ $$$${note}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{e}^{{x}} }\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{e}^{−{x}} \:=\:\mathrm{0} \\ $$$${L}=\frac{\mathrm{2}+\mathrm{0}.\mathrm{ln}\left(\mathrm{3}+\mathrm{0}−\mathrm{0}\right)}{\mathrm{3}+\mathrm{0}.\mathrm{ln}\left(\mathrm{27}−\mathrm{0}\right)}\:=\:\frac{\mathrm{2}}{\mathrm{3}}.\:\left(\oplus\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com