Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 103492 by abony1303 last updated on 15/Jul/20

Q1: Evaluate ∫_(−1) ^( 1) ∣x∣∙(x^3 +1)dx Q2: Find the sum of all integers k for which the equation 2x^3 −6x^2 +k=0 has more than one solution. Q3: Find the shortest distance from a point on the curve y=x^2 −x to the line y=x−3

$$\mathrm{Q1}:\:\:\mathrm{Evaluate}\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} \mid\mathrm{x}\mid\centerdot\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)\mathrm{dx} \\ $$$$ \\ $$$$\mathrm{Q2}:\:\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{integers}\:{k}\:\mathrm{for}\: \\ $$$$\mathrm{which}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{2}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +{k}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{more}\:\mathrm{than}\:\mathrm{one}\:\mathrm{solution}. \\ $$$$ \\ $$$$\mathrm{Q3}:\:\mathrm{Find}\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{from}\:\mathrm{a}\: \\ $$$$\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{curve}\:{y}={x}^{\mathrm{2}} −{x}\:\mathrm{to}\:\mathrm{the}\:\mathrm{line} \\ $$$${y}={x}−\mathrm{3} \\ $$

Commented by abony1303 last updated on 15/Jul/20

pls help

$$\mathrm{pls}\:\mathrm{help} \\ $$

Answered by mr W last updated on 15/Jul/20

Q2 2x^2 (x−3)+k=0 k<0 ⇒one root: x>3 k=0 ⇒two roots: x=0 or 3 k>0: (1/x^3 )−(6/(kx))+(2/k)=0 such that three roots: ((1/k))^2 +(−(2/k))^3 <0 ((1/k))^2 (1−(8/k))<0 1−(8/k)<0 k<8 ⇒k=1,2,3,...,7 Σk=((7(1+7))/2)=28

$${Q}\mathrm{2} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} \left({x}−\mathrm{3}\right)+{k}=\mathrm{0} \\ $$$${k}<\mathrm{0}\:\Rightarrow{one}\:{root}:\:{x}>\mathrm{3} \\ $$$${k}=\mathrm{0}\:\Rightarrow{two}\:{roots}:\:{x}=\mathrm{0}\:{or}\:\mathrm{3} \\ $$$${k}>\mathrm{0}: \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\frac{\mathrm{6}}{{kx}}+\frac{\mathrm{2}}{{k}}=\mathrm{0} \\ $$$${such}\:{that}\:{three}\:{roots}: \\ $$$$\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} +\left(−\frac{\mathrm{2}}{{k}}\right)^{\mathrm{3}} <\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{8}}{{k}}\right)<\mathrm{0} \\ $$$$\mathrm{1}−\frac{\mathrm{8}}{{k}}<\mathrm{0} \\ $$$${k}<\mathrm{8} \\ $$$$\Rightarrow{k}=\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{7} \\ $$$$\Sigma{k}=\frac{\mathrm{7}\left(\mathrm{1}+\mathrm{7}\right)}{\mathrm{2}}=\mathrm{28} \\ $$

Commented by abony1303 last updated on 15/Jul/20

thank you sir. but I drew a graph and k=8 also correct? And pls can you explain the raw such that three roots... and below it.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{but}\:\mathrm{I}\:\mathrm{drew}\:\mathrm{a}\:\mathrm{graph}\:\mathrm{and}\:\mathrm{k}=\mathrm{8} \\ $$$$\mathrm{also}\:\mathrm{correct}?\:\mathrm{And}\:\mathrm{pls}\:\mathrm{can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{the} \\ $$$$\mathrm{raw}\:{such}\:{that}\:{three}\:{roots}...\:{and}\:\mathrm{below}\:{it}. \\ $$

Commented by mr W last updated on 15/Jul/20

i misread the question as: more than two roots. for more than one root: the answer is Σk=0+1+2+3+...+8=36 we have: (1/x^3 )−(6/(kx))+(2/k)=0 let t=(1/x), then t^3 −(6/k)t+(2/k)=0 three roots for x ⇒ three roots for t. let f(t)=t^3 +bt+c if f(t)=0 has three roots, it means f′(t)=0 ⇒3t^2 +b=0⇒t_(1,2) =±(√(−(b/3))) f(t_1 )f(t_2 )<0, see diagram. f(t_1 )=t_1 ^3 +bt_1 +c=(1/3)t_1 (3t_1 ^2 +b)+((2bt_1 )/3)+c=((2bt_1 )/3)+c f(t_2 )=((2bt_2 )/3)+c (((2bt_1 )/3)+c)(((2bt_2 )/3)+c)<0 ((4b^2 )/9)t_1 t_2 +((2b)/3)(t_1 +t_2 )+c^2 <0 ((4b^2 )/9)×(b/3)+((2b)/3)×0+c^2 <0 ⇒((b/3))^3 +((c/2))^2 <0 with b=−(6/k), c=(2/k) ⇒(−(2/k))^3 +((1/k))^2 <0

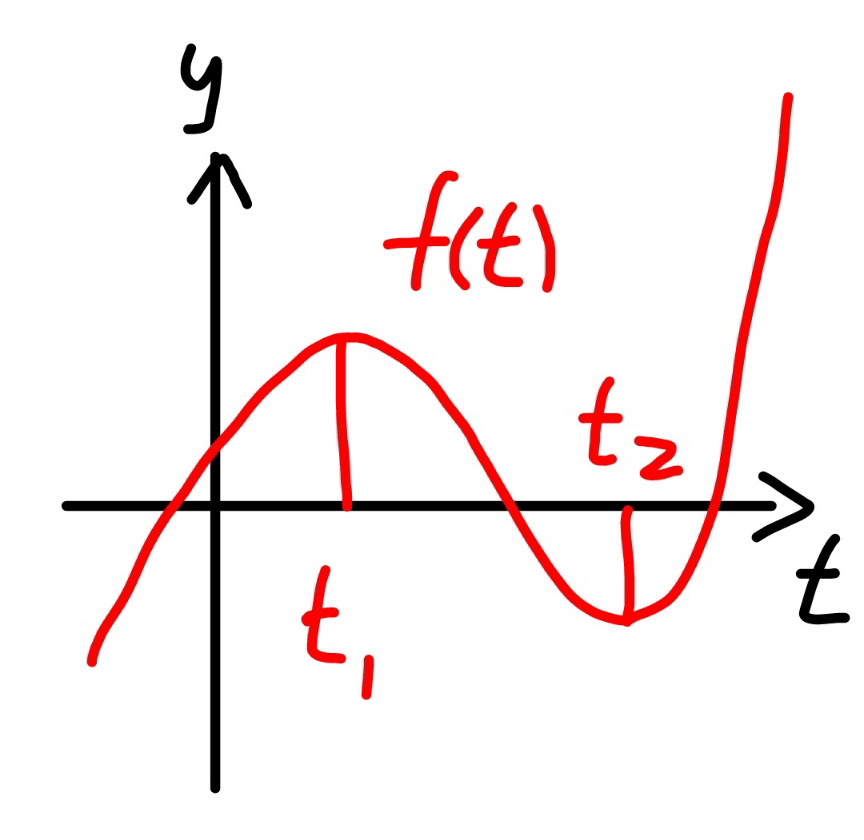
$${i}\:{misread}\:{the}\:{question}\:{as}:\:{more}\:{than} \\ $$$${two}\:{roots}. \\ $$$${for}\:{more}\:{than}\:{one}\:{root}:\:{the}\:{answer} \\ $$$${is}\:\Sigma{k}=\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{8}=\mathrm{36} \\ $$$$ \\ $$$${we}\:{have}: \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\frac{\mathrm{6}}{{kx}}+\frac{\mathrm{2}}{{k}}=\mathrm{0} \\ $$$${let}\:{t}=\frac{\mathrm{1}}{{x}},\:{then} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{6}}{{k}}{t}+\frac{\mathrm{2}}{{k}}=\mathrm{0} \\ $$$${three}\:{roots}\:{for}\:{x}\:\Rightarrow\:{three}\:{roots}\:{for}\:{t}. \\ $$$$ \\ $$$${let}\:{f}\left({t}\right)={t}^{\mathrm{3}} +{bt}+{c} \\ $$$${if}\:{f}\left({t}\right)=\mathrm{0}\:{has}\:{three}\:{roots},\:{it}\:{means} \\ $$$${f}'\left({t}\right)=\mathrm{0}\:\Rightarrow\mathrm{3}{t}^{\mathrm{2}} +{b}=\mathrm{0}\Rightarrow{t}_{\mathrm{1},\mathrm{2}} =\pm\sqrt{−\frac{{b}}{\mathrm{3}}} \\ $$$${f}\left({t}_{\mathrm{1}} \right){f}\left({t}_{\mathrm{2}} \right)<\mathrm{0},\:{see}\:{diagram}. \\ $$$${f}\left({t}_{\mathrm{1}} \right)={t}_{\mathrm{1}} ^{\mathrm{3}} +{bt}_{\mathrm{1}} +{c}=\frac{\mathrm{1}}{\mathrm{3}}{t}_{\mathrm{1}} \left(\mathrm{3}{t}_{\mathrm{1}} ^{\mathrm{2}} +{b}\right)+\frac{\mathrm{2}{bt}_{\mathrm{1}} }{\mathrm{3}}+{c}=\frac{\mathrm{2}{bt}_{\mathrm{1}} }{\mathrm{3}}+{c} \\ $$$${f}\left({t}_{\mathrm{2}} \right)=\frac{\mathrm{2}{bt}_{\mathrm{2}} }{\mathrm{3}}+{c} \\ $$$$\left(\frac{\mathrm{2}{bt}_{\mathrm{1}} }{\mathrm{3}}+{c}\right)\left(\frac{\mathrm{2}{bt}_{\mathrm{2}} }{\mathrm{3}}+{c}\right)<\mathrm{0} \\ $$$$\frac{\mathrm{4}{b}^{\mathrm{2}} }{\mathrm{9}}{t}_{\mathrm{1}} {t}_{\mathrm{2}} +\frac{\mathrm{2}{b}}{\mathrm{3}}\left({t}_{\mathrm{1}} +{t}_{\mathrm{2}} \right)+{c}^{\mathrm{2}} <\mathrm{0} \\ $$$$\frac{\mathrm{4}{b}^{\mathrm{2}} }{\mathrm{9}}×\frac{{b}}{\mathrm{3}}+\frac{\mathrm{2}{b}}{\mathrm{3}}×\mathrm{0}+{c}^{\mathrm{2}} <\mathrm{0} \\ $$$$\Rightarrow\left(\frac{{b}}{\mathrm{3}}\right)^{\mathrm{3}} +\left(\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} <\mathrm{0} \\ $$$${with}\:{b}=−\frac{\mathrm{6}}{{k}},\:{c}=\frac{\mathrm{2}}{{k}} \\ $$$$\Rightarrow\left(−\frac{\mathrm{2}}{{k}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} <\mathrm{0} \\ $$

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

Commented by mr W last updated on 15/Jul/20

three roots only for 1≤k≤7. two roots only for k=0 or 8. one root only for k≤−1 or k≥9.

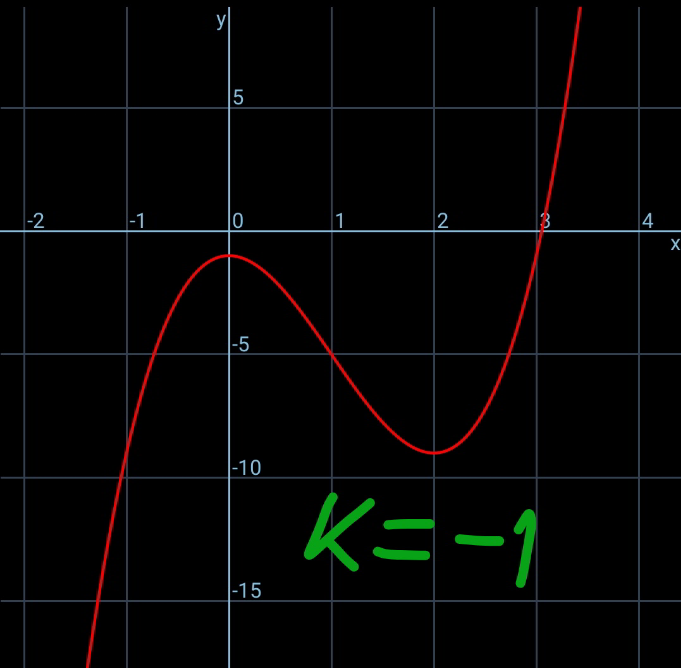
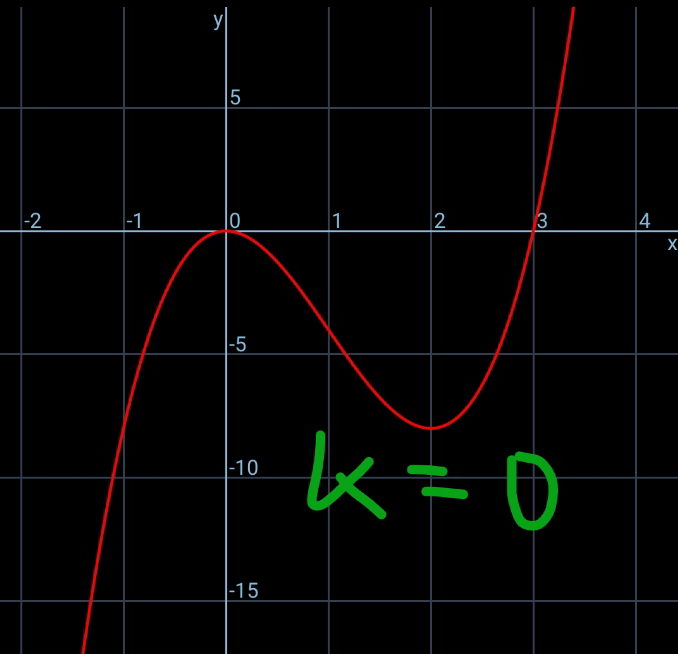
$${three}\:{roots}\:{only}\:{for}\:\mathrm{1}\leqslant{k}\leqslant\mathrm{7}. \\ $$$${two}\:{roots}\:{only}\:{for}\:{k}=\mathrm{0}\:{or}\:\mathrm{8}. \\ $$$${one}\:{root}\:{only}\:{for}\:{k}\leqslant−\mathrm{1}\:{or}\:{k}\geqslant\mathrm{9}. \\ $$

Answered by mr W last updated on 15/Jul/20

Q3 y=x^2 −x y′=2x−1=1 ⇒x=1, y=0 d_(min) =((∣1×1−1×0−3∣)/(√(1^2 +(−1)^2 )))=(√2)

$${Q}\mathrm{3} \\ $$$${y}={x}^{\mathrm{2}} −{x} \\ $$$${y}'=\mathrm{2}{x}−\mathrm{1}=\mathrm{1}\:\Rightarrow{x}=\mathrm{1},\:{y}=\mathrm{0} \\ $$$${d}_{{min}} =\frac{\mid\mathrm{1}×\mathrm{1}−\mathrm{1}×\mathrm{0}−\mathrm{3}\mid}{\sqrt{\mathrm{1}^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} }}=\sqrt{\mathrm{2}} \\ $$

Answered by mr W last updated on 15/Jul/20

Q1 ∫_(−1) ^( 1) ∣x∣∙(x^3 +1)dx =∫_(−1) ^( 1) ∣x∣∙x^3 dx+∫_(−1) ^( 1) ∣x∣dx =0+2∫_0 ^( 1) xdx =1

$${Q}\mathrm{1} \\ $$$$\int_{−\mathrm{1}} ^{\:\mathrm{1}} \mid\mathrm{x}\mid\centerdot\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)\mathrm{dx} \\ $$$$=\int_{−\mathrm{1}} ^{\:\mathrm{1}} \mid\mathrm{x}\mid\centerdot\mathrm{x}^{\mathrm{3}} \mathrm{dx}+\int_{−\mathrm{1}} ^{\:\mathrm{1}} \mid\mathrm{x}\mid\mathrm{dx} \\ $$$$=\mathrm{0}+\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{xdx} \\ $$$$=\mathrm{1} \\ $$

Answered by OlafThorendsen last updated on 15/Jul/20

Q1. I = ∫_(−1) ^1 ∣x∣(x^3 +1)dx I = ∫_(−1) ^0 −x(x^3 +1)dx+∫_0 ^1 x(x^3 +1)dx I = [−(x^5 /5)−(x^2 /2)]_(−1) ^0 +[(x^5 /5)+(x^2 /2)]_0 ^1 I = (−(1/5)+(1/2))+((1/5)+(1/2)) I = 1 Q2. Δ′ = (−3)^2 −(2)(k) = 9−2k More than one solution ⇔ Δ′>0 ⇔ k<(9/2) ⇔ k∈{0;1;2;3;4} ⇒ sum = 0+1+2+3+4 = 10 Q3. A is a point of the curve B is a point of the line A ((a),((a^2 −a)) ) and B ((b),((b−3)) ) AB^2 = (b−a)^2 +(b−3−a^2 +a)^2 for a given a, AB^2 = f(b) f(b) = (b−a)^2 +(b−3−a^2 +a)^2 f′(b) = 2(b−a)+2(b−3−a^2 +a) f′(b) = 4b−2a^2 −6 f′(b) = 0 ⇔ b = ((a^2 +3)/2) Then : AB^2 = (((a^2 +3)/2)−a)^2 +(((a^2 +3)/2)−3−a^2 +a)^2 AB^2 = ((a^2 /2)−a+(3/2))^2 +(−(a^2 /2)+a−(3/2))^2 AB^2 = 2((a^2 /2)−a+(3/2))^2 AB = (√2)∣(a^2 /2)−a+(3/2)∣ and then : A ((a),((a^2 −a)) ) and B ((((a^2 +3)/2)),(((a^2 −3)/2)) )

$$\mathrm{Q1}. \\ $$$$\mathrm{I}\:=\:\int_{−\mathrm{1}} ^{\mathrm{1}} \mid{x}\mid\left({x}^{\mathrm{3}} +\mathrm{1}\right){dx} \\ $$$$\mathrm{I}\:=\:\int_{−\mathrm{1}} ^{\mathrm{0}} −{x}\left({x}^{\mathrm{3}} +\mathrm{1}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left({x}^{\mathrm{3}} +\mathrm{1}\right){dx} \\ $$$$\mathrm{I}\:=\:\left[−\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{−\mathrm{1}} ^{\mathrm{0}} +\left[\frac{{x}^{\mathrm{5}} }{\mathrm{5}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\left(−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{I}\:=\:\mathrm{1} \\ $$$$\mathrm{Q2}. \\ $$$$\Delta'\:=\:\left(−\mathrm{3}\right)^{\mathrm{2}} −\left(\mathrm{2}\right)\left({k}\right)\:=\:\mathrm{9}−\mathrm{2}{k} \\ $$$$\mathrm{More}\:\mathrm{than}\:\mathrm{one}\:\mathrm{solution}\:\Leftrightarrow\:\Delta'>\mathrm{0} \\ $$$$\Leftrightarrow\:{k}<\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\Leftrightarrow\:{k}\in\left\{\mathrm{0};\mathrm{1};\mathrm{2};\mathrm{3};\mathrm{4}\right\} \\ $$$$\Rightarrow\:\mathrm{sum}\:=\:\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}\:=\:\mathrm{10} \\ $$$$\mathrm{Q3}. \\ $$$$\mathrm{A}\:\mathrm{is}\:\mathrm{a}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\mathrm{B}\:\mathrm{is}\:\mathrm{a}\:\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line} \\ $$$$\mathrm{A}\begin{pmatrix}{{a}}\\{{a}^{\mathrm{2}} −{a}}\end{pmatrix}\:\mathrm{and}\:\mathrm{B}\begin{pmatrix}{{b}}\\{{b}−\mathrm{3}}\end{pmatrix} \\ $$$$\mathrm{AB}^{\mathrm{2}} \:=\:\left({b}−{a}\right)^{\mathrm{2}} +\left({b}−\mathrm{3}−{a}^{\mathrm{2}} +{a}\right)^{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{a}\:\mathrm{given}\:{a},\:\mathrm{AB}^{\mathrm{2}} \:=\:{f}\left({b}\right) \\ $$$${f}\left({b}\right)\:=\:\left({b}−{a}\right)^{\mathrm{2}} +\left({b}−\mathrm{3}−{a}^{\mathrm{2}} +{a}\right)^{\mathrm{2}} \\ $$$${f}'\left({b}\right)\:=\:\mathrm{2}\left({b}−{a}\right)+\mathrm{2}\left({b}−\mathrm{3}−{a}^{\mathrm{2}} +{a}\right) \\ $$$${f}'\left({b}\right)\:=\:\mathrm{4}{b}−\mathrm{2}{a}^{\mathrm{2}} −\mathrm{6} \\ $$$${f}'\left({b}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:{b}\:=\:\frac{{a}^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{Then}\:: \\ $$$$\mathrm{AB}^{\mathrm{2}} \:=\:\left(\frac{{a}^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}}−{a}\right)^{\mathrm{2}} +\left(\frac{{a}^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}}−\mathrm{3}−{a}^{\mathrm{2}} +{a}\right)^{\mathrm{2}} \\ $$$$\mathrm{AB}^{\mathrm{2}} \:=\:\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−{a}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{a}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{AB}^{\mathrm{2}} \:=\:\mathrm{2}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−{a}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{AB}\:=\:\sqrt{\mathrm{2}}\mid\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−{a}+\frac{\mathrm{3}}{\mathrm{2}}\mid\:\mathrm{and}\:\mathrm{then}\:: \\ $$$$\mathrm{A}\begin{pmatrix}{{a}}\\{{a}^{\mathrm{2}} −{a}}\end{pmatrix}\:\:\mathrm{and}\:\mathrm{B}\begin{pmatrix}{\frac{{a}^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}}}\\{\frac{{a}^{\mathrm{2}} −\mathrm{3}}{\mathrm{2}}}\end{pmatrix} \\ $$

Commented by abony1303 last updated on 15/Jul/20

no, no it′s ok. :)

$$\left.\mathrm{no},\:\mathrm{no}\:\mathrm{it}'\mathrm{s}\:\mathrm{ok}.\::\right)\: \\ $$

Commented by OlafThorendsen last updated on 15/Jul/20

sorry ! I need to change my glasses ! :−)

$$\mathrm{sorry}\:!\:\mathrm{I}\:\mathrm{need}\:\mathrm{to}\:\mathrm{change}\:\mathrm{my} \\ $$$$\left.\mathrm{glasses}\:!\::−\right) \\ $$

Commented by abony1303 last updated on 15/Jul/20

Thank you ser.Everything is clear, but can you pls explain what is △′ in Q2?

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{ser}.\mathrm{Everything}\:\mathrm{is}\:\mathrm{clear},\:\mathrm{but}\: \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{pls}\:\mathrm{explain}\:\mathrm{what}\:\mathrm{is}\:\bigtriangleup'\:\mathrm{in}\:\mathrm{Q2}? \\ $$

Commented by bemath last updated on 15/Jul/20

Δ = b^2 −4ac discriminant

$$\Delta\:=\:{b}^{\mathrm{2}} −\mathrm{4}{ac}\: \\ $$$${discriminant} \\ $$

Commented by abony1303 last updated on 15/Jul/20

but it′s not the quadratic equation?

$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{equation}? \\ $$

Commented by OlafThorendsen last updated on 15/Jul/20

Δ′ : reduced discriminant (sorry my english is not fluent) x = ((−b±(√Δ))/(2a)) with Δ = b^2 −4ac but when b is even you can use : x = ((−b′±(√(Δ′)))/a) with b′ = (b/2) and Δ′ = b′^2 −ac (the calculation is faster)

$$\Delta'\::\:\mathrm{reduced}\:\mathrm{discriminant} \\ $$$$\left(\mathrm{sorry}\:\mathrm{my}\:\mathrm{english}\:\mathrm{is}\:\mathrm{not}\:\mathrm{fluent}\right) \\ $$$${x}\:=\:\frac{−{b}\pm\sqrt{\Delta}}{\mathrm{2}{a}}\:\mathrm{with}\:\Delta\:=\:{b}^{\mathrm{2}} −\mathrm{4}{ac} \\ $$$$\mathrm{but}\:\mathrm{when}\:{b}\:\mathrm{is}\:\mathrm{even}\:\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:: \\ $$$${x}\:=\:\frac{−{b}'\pm\sqrt{\Delta'}}{{a}} \\ $$$$\mathrm{with}\:{b}'\:=\:\frac{{b}}{\mathrm{2}}\:\mathrm{and}\:\Delta'\:=\:{b}'^{\mathrm{2}} −{ac} \\ $$$$\left(\mathrm{the}\:\mathrm{calculation}\:\mathrm{is}\:\mathrm{faster}\right) \\ $$

Commented by abony1303 last updated on 15/Jul/20

ser but it′s not the quadratic equation?

$$\mathrm{ser}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{equation}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com