Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 103510 by 175mohamed last updated on 15/Jul/20

Commented by Worm_Tail last updated on 15/Jul/20

y=cot^(−1) (x)⇒cot(y)=x tan(y)=(1/x)⇒y=tan^(−1) (1/x) cot^(−1) x=tan^(−1) (1/x) my plot down the comment from geogebra

$${y}={cot}^{−\mathrm{1}} \left({x}\right)\Rightarrow{cot}\left({y}\right)={x} \\ $$$${tan}\left({y}\right)=\frac{\mathrm{1}}{{x}}\Rightarrow{y}={tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}} \\ $$$${cot}^{−\mathrm{1}} {x}={tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}} \\ $$$$ \\ $$$${my}\:\:\:{plot}\:\:\:{down}\:\:\:\:{the}\:\:{comment}\:\:{from}\:\:\:{geogebra} \\ $$$$ \\ $$

Commented by Worm_Tail last updated on 15/Jul/20

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

∵ both are periodic functions but the both do not have the same period of interval. the inverse of tan will be in the domain of −(π/2) to (π/2) and for the cot it is from 0 to π ∴ you can′t replace cot^(−1) by tan^(−1) ((1/x)) in the 0 to −∞ domain.

$$\because\:\mathrm{both}\:\mathrm{are}\:\mathrm{periodic}\:\mathrm{functions}\:\mathrm{but}\:\mathrm{the}\:\mathrm{both}\:\mathrm{do}\:\mathrm{not} \\ $$$$\mathrm{have}\:\mathrm{the}\:\mathrm{same}\:\mathrm{period}\:\mathrm{of}\:\mathrm{interval}. \\ $$$$\mathrm{the}\:\mathrm{inverse}\:\mathrm{of}\:\mathrm{tan}\:\mathrm{will}\:\mathrm{be}\:\mathrm{in}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\: \\ $$$$−\frac{\pi}{\mathrm{2}}\:\mathrm{to}\:\frac{\pi}{\mathrm{2}}\:\mathrm{and}\:\mathrm{for}\:\mathrm{the}\:\mathrm{cot}\:\mathrm{it}\:\mathrm{is}\:\mathrm{from}\:\mathrm{0}\:\mathrm{to}\:\pi \\ $$$$\therefore\:\mathrm{you}\:\mathrm{can}'\mathrm{t}\:\mathrm{replace}\:\mathrm{cot}^{−\mathrm{1}} \:\mathrm{by}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{0}\:\mathrm{to}\:−\infty\:\mathrm{domain}. \\ $$

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

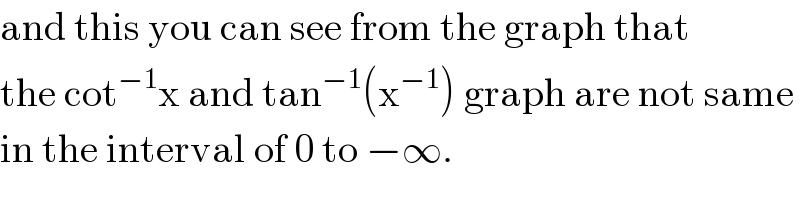
and this you can see from the graph that the cot^(−1) x and tan^(−1) (x^(−1) ) graph are not same in the interval of 0 to −∞.

$$\mathrm{and}\:\mathrm{this}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{from}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{that}\: \\ $$$$\mathrm{the}\:\mathrm{cot}^{−\mathrm{1}} \mathrm{x}\:\mathrm{and}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}^{−\mathrm{1}} \right)\:\mathrm{graph}\:\mathrm{are}\:\mathrm{not}\:\mathrm{same} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{interval}\:\mathrm{of}\:\mathrm{0}\:\mathrm{to}\:−\infty. \\ $$

Commented by abdomathmax last updated on 16/Jul/20

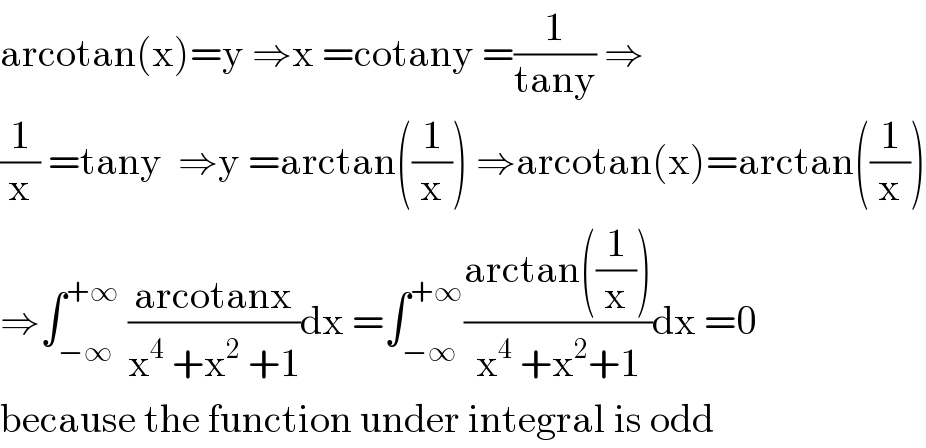
arcotan(x)=y ⇒x =cotany =(1/(tany)) ⇒ (1/x) =tany ⇒y =arctan((1/x)) ⇒arcotan(x)=arctan((1/x)) ⇒∫_(−∞) ^(+∞) ((arcotanx)/(x^4 +x^2 +1))dx =∫_(−∞) ^(+∞) ((arctan((1/x)))/(x^4 +x^2 +1))dx =0 because the function under integral is odd

$$\mathrm{arcotan}\left(\mathrm{x}\right)=\mathrm{y}\:\Rightarrow\mathrm{x}\:=\mathrm{cotany}\:=\frac{\mathrm{1}}{\mathrm{tany}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}\:=\mathrm{tany}\:\:\Rightarrow\mathrm{y}\:=\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\Rightarrow\mathrm{arcotan}\left(\mathrm{x}\right)=\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\frac{\mathrm{arcotanx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{−\infty} ^{+\infty} \frac{\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\mathrm{0} \\ $$$$\mathrm{because}\:\mathrm{the}\:\mathrm{function}\:\mathrm{under}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{odd} \\ $$

Answered by Worm_Tail last updated on 15/Jul/20

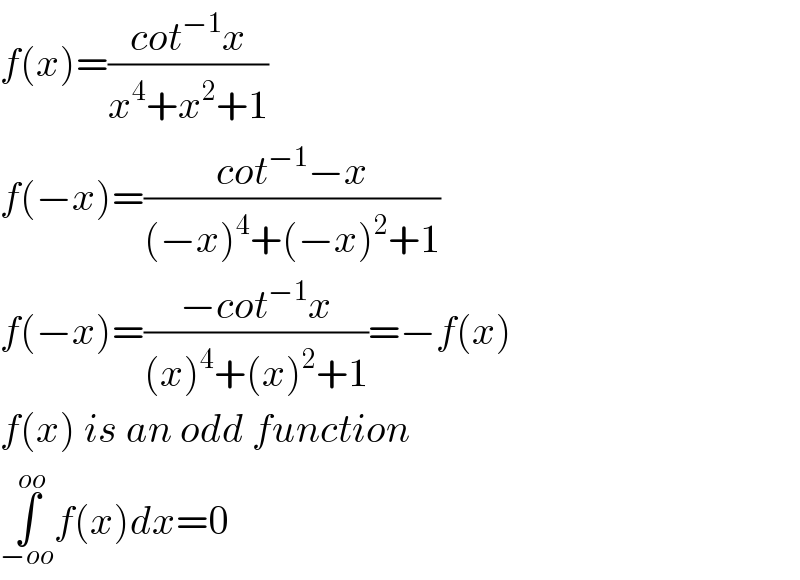
f(x)=((cot^(−1) x)/(x^4 +x^2 +1)) f(−x)=((cot^(−1) −x)/((−x)^4 +(−x)^2 +1)) f(−x)=((−cot^(−1) x)/((x)^4 +(x)^2 +1))=−f(x) f(x) is an odd function ∫_(−oo) ^(oo) f(x)dx=0

$${f}\left({x}\right)=\frac{{cot}^{−\mathrm{1}} {x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\left(−{x}\right)=\frac{{cot}^{−\mathrm{1}} −{x}}{\left(−{x}\right)^{\mathrm{4}} +\left(−{x}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\left(−{x}\right)=\frac{−{cot}^{−\mathrm{1}} {x}}{\left({x}\right)^{\mathrm{4}} +\left({x}\right)^{\mathrm{2}} +\mathrm{1}}=−{f}\left({x}\right) \\ $$$${f}\left({x}\right)\:{is}\:{an}\:{odd}\:{function} \\ $$$$\underset{−{oo}} {\overset{{oo}} {\int}}{f}\left({x}\right){dx}=\mathrm{0} \\ $$

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

it is not an odd function

$$\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function} \\ $$

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

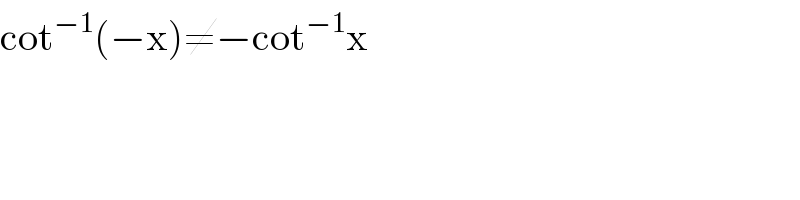
cot^(−1) (−x)≠−cot^(−1) x

$$\mathrm{cot}^{−\mathrm{1}} \left(−\mathrm{x}\right)\neq−\mathrm{cot}^{−\mathrm{1}} \mathrm{x} \\ $$

Commented by PRITHWISH SEN 2 last updated on 15/Jul/20

Commented by Worm_Tail last updated on 15/Jul/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com