Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 103511 by bemath last updated on 15/Jul/20

∫ (dx/((√x) ((x)^(1/4) +1))) =__ (a) −((9 (x)^(1/4) +1)/(18((x)^(1/4) +1)^9 )) + c (b) ((9 (x)^(1/4) +1)/(18((x)^(1/4) +1)^9 )) +c (c) −((9 (x)^(1/4) −1)/(18((x)^(1/4) +1)^9 )) +c (d) ((9 (x)^(1/4) +1)/(8((x)^(1/4) +1)^9 )) + c

$$\int\:\frac{{dx}}{\sqrt{{x}}\:\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)}\:=\_\_ \\ $$$$\left({a}\right)\:−\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}}{\mathrm{18}\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)^{\mathrm{9}} }\:+\:{c}\: \\ $$$$\left({b}\right)\:\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}}{\mathrm{18}\left(\sqrt[{\mathrm{4}}]{{x}}+\mathrm{1}\right)^{\mathrm{9}} }\:+{c} \\ $$$$\left({c}\right)\:−\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}\:−\mathrm{1}}{\mathrm{18}\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)^{\mathrm{9}} }\:+{c} \\ $$$$\left({d}\right)\:\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}+\mathrm{1}}{\mathrm{8}\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)^{\mathrm{9}} }\:+\:{c} \\ $$

Commented by bobhans last updated on 15/Jul/20

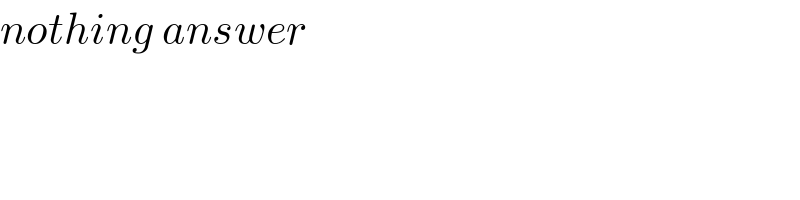
nothing answer

$${nothing}\:{answer} \\ $$

Answered by bramlex last updated on 15/Jul/20

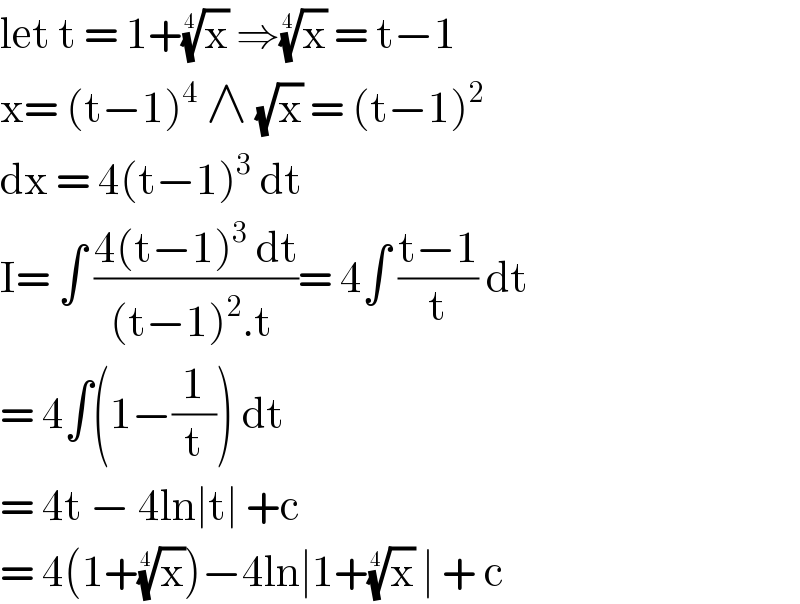
let t = 1+(x)^(1/4) ⇒(x)^(1/4) = t−1 x= (t−1)^4 ∧ (√x) = (t−1)^2 dx = 4(t−1)^3 dt I= ∫ ((4(t−1)^3 dt)/((t−1)^2 .t ))= 4∫ ((t−1)/t) dt = 4∫(1−(1/t)) dt = 4t − 4ln∣t∣ +c = 4(1+(x)^(1/4) )−4ln∣1+(x)^(1/4) ∣ + c

$$\mathrm{let}\:\mathrm{t}\:=\:\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\Rightarrow\sqrt[{\mathrm{4}}]{\mathrm{x}}\:=\:\mathrm{t}−\mathrm{1} \\ $$$$\mathrm{x}=\:\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} \:\wedge\:\sqrt{\mathrm{x}}\:=\:\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{dx}\:=\:\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{3}} \:\mathrm{dt}\: \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{3}} \:\mathrm{dt}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} .\mathrm{t}\:}=\:\mathrm{4}\int\:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}}\:\mathrm{dt} \\ $$$$=\:\mathrm{4}\int\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}}\right)\:\mathrm{dt}\: \\ $$$$=\:\mathrm{4t}\:−\:\mathrm{4ln}\mid\mathrm{t}\mid\:+\mathrm{c}\: \\ $$$$=\:\mathrm{4}\left(\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{x}}\right)−\mathrm{4ln}\mid\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\mid\:+\:\mathrm{c}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com