Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 103512 by bemath last updated on 15/Jul/20

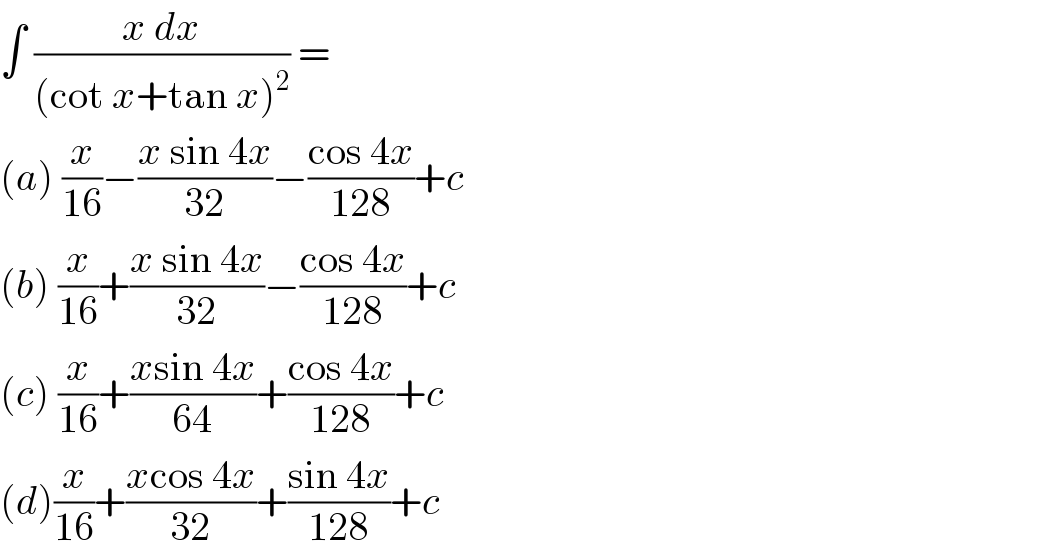
∫ ((x dx)/((cot x+tan x)^2 )) = (a) (x/(16))−((x sin 4x)/(32))−((cos 4x)/(128))+c (b) (x/(16))+((x sin 4x)/(32))−((cos 4x)/(128))+c (c) (x/(16))+((xsin 4x)/(64))+((cos 4x)/(128))+c (d)(x/(16))+((xcos 4x)/(32))+((sin 4x)/(128))+c

$$\int\:\frac{{x}\:{dx}}{\left(\mathrm{cot}\:{x}+\mathrm{tan}\:{x}\right)^{\mathrm{2}} }\:= \\ $$$$\left({a}\right)\:\frac{{x}}{\mathrm{16}}−\frac{{x}\:\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{32}}−\frac{\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{128}}+{c} \\ $$$$\left({b}\right)\:\frac{{x}}{\mathrm{16}}+\frac{{x}\:\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{32}}−\frac{\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{128}}+{c} \\ $$$$\left({c}\right)\:\frac{{x}}{\mathrm{16}}+\frac{{x}\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{64}}+\frac{\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{128}}+{c} \\ $$$$\left({d}\right)\frac{{x}}{\mathrm{16}}+\frac{{x}\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{32}}+\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{128}}+{c} \\ $$

Commented by bobhans last updated on 15/Jul/20

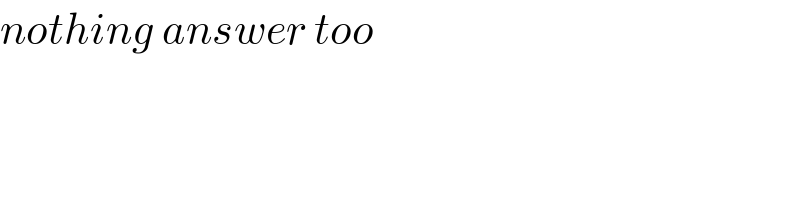
nothing answer too

$${nothing}\:{answer}\:{too} \\ $$

Commented by bemath last updated on 15/Jul/20

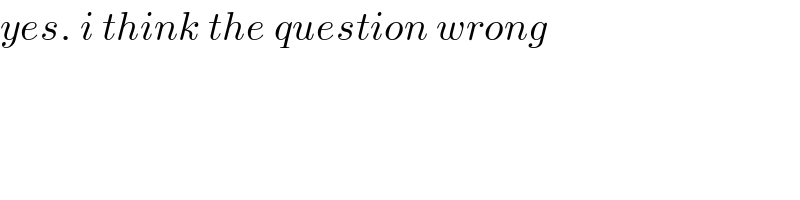
yes. i think the question wrong

$${yes}.\:{i}\:{think}\:{the}\:{question}\:{wrong} \\ $$

Answered by Dwaipayan Shikari last updated on 15/Jul/20

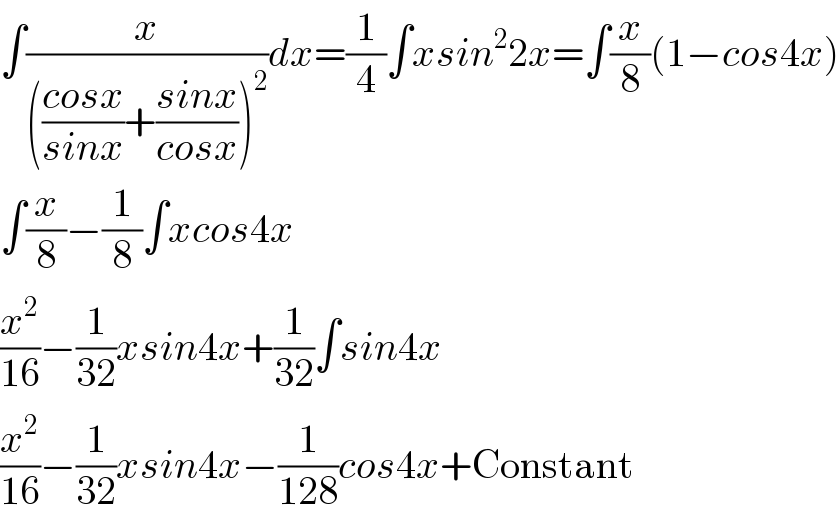
∫(x/((((cosx)/(sinx))+((sinx)/(cosx)))^2 ))dx=(1/4)∫xsin^2 2x=∫(x/8)(1−cos4x) ∫(x/8)−(1/8)∫xcos4x (x^2 /(16))−(1/(32))xsin4x+(1/(32))∫sin4x (x^2 /(16))−(1/(32))xsin4x−(1/(128))cos4x+Constant

$$\int\frac{{x}}{\left(\frac{{cosx}}{{sinx}}+\frac{{sinx}}{{cosx}}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int{xsin}^{\mathrm{2}} \mathrm{2}{x}=\int\frac{{x}}{\mathrm{8}}\left(\mathrm{1}−{cos}\mathrm{4}{x}\right) \\ $$$$\int\frac{{x}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}\int{xcos}\mathrm{4}{x} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{32}}{xsin}\mathrm{4}{x}+\frac{\mathrm{1}}{\mathrm{32}}\int{sin}\mathrm{4}{x} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{32}}{xsin}\mathrm{4}{x}−\frac{\mathrm{1}}{\mathrm{128}}{cos}\mathrm{4}{x}+\mathrm{Constant} \\ $$

Answered by bramlex last updated on 15/Jul/20

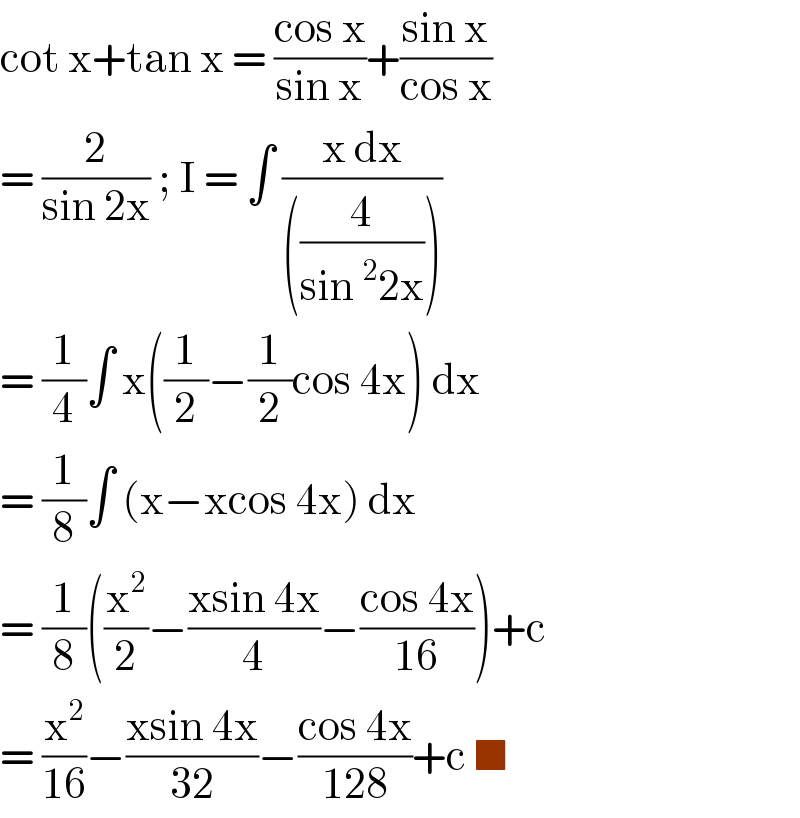
cot x+tan x = ((cos x)/(sin x))+((sin x)/(cos x)) = (2/(sin 2x)) ; I = ∫ ((x dx)/(((4/(sin^2 2x))))) = (1/4)∫ x((1/2)−(1/2)cos 4x) dx = (1/8)∫ (x−xcos 4x) dx = (1/8)((x^2 /2)−((xsin 4x)/4)−((cos 4x)/(16)))+c = (x^2 /(16))−((xsin 4x)/(32))−((cos 4x)/(128))+c ■

$$\mathrm{cot}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\:=\:\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}+\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{2x}}\:;\:\mathrm{I}\:=\:\int\:\frac{\mathrm{x}\:\mathrm{dx}}{\left(\frac{\mathrm{4}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4x}\right)\:\mathrm{dx}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\int\:\left(\mathrm{x}−\mathrm{xcos}\:\mathrm{4x}\right)\:\mathrm{dx}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{xsin}\:\mathrm{4x}}{\mathrm{4}}−\frac{\mathrm{cos}\:\mathrm{4x}}{\mathrm{16}}\right)+\mathrm{c} \\ $$$$=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{xsin}\:\mathrm{4x}}{\mathrm{32}}−\frac{\mathrm{cos}\:\mathrm{4x}}{\mathrm{128}}+\mathrm{c}\:\blacksquare \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com