Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 103537 by TMSF last updated on 15/Jul/20

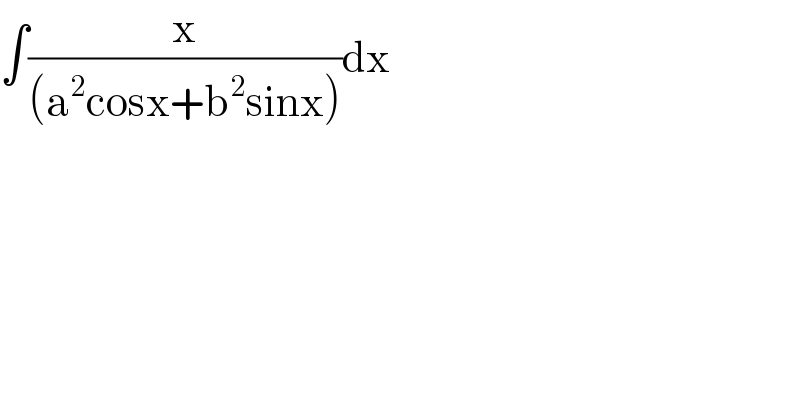
$$\int \frac{\mathrm{x}}{({\mathrm{a}}^2\mathrm{cosx}+{\mathrm{b}}^2\mathrm{sinx})}\mathrm{dx}$$

Answered by mathmax by abdo last updated on 15/Jul/20

$$\mathrm{let}\mathrm{I}=\int \frac{\mathrm{xdx}}{{\mathrm{a}}^2\mathrm{cosx}+{\mathrm{b}}^2\mathrm{sinx}}\mathrm{we}\mathrm{put}{\mathrm{a}}^2=\alpha \mathrm{and}{\mathrm{b}}^2=\beta \Rightarrow$$$$\mathrm{I}=\int \frac{\mathrm{xdx}}{\alpha \mathrm{cosx}+\beta \mathrm{sinx}}\mathrm{changement}\tan \left(\frac{\mathrm{x}}{2}\right)=\mathrm{t}\mathrm{give}$$$$\mathrm{I}=\int \frac{2\arctan \left(\mathrm{t}\right)}{\alpha \times \frac{1-{\mathrm{t}}^2}{1+{\mathrm{t}}^2}+\beta \times \frac{2\mathrm{t}}{1+{\mathrm{t}}^2}}\times \frac{2\mathrm{dt}}{1+{\mathrm{t}}^2}$$$$=4\int \frac{\arctan \left(\mathrm{t}\right)}{\alpha -\alpha {\mathrm{t}}^2+2\beta \mathrm{t}}\mathrm{dt}=-4\int \frac{\arctan \left(\mathrm{t}\right)}{\alpha {\mathrm{t}}^2-2\beta \mathrm{t}-\alpha }\mathrm{dt}$$$$\mathrm{let}\mathrm{f}\left(\xi \right)=\int \frac{\arctan \left(\xi \mathrm{t}\right)}{\alpha {\mathrm{t}}^2-2\beta \mathrm{t}-\alpha }\mathrm{dt}\mathrm{we}\mathrm{have}$$$${\mathrm{f}}^{{}^{\prime }}\left(\xi \right)=\int \frac{\mathrm{t}}{(1+{\xi }^2{\mathrm{t}}^2)(\alpha {\mathrm{t}}^2-2\beta \mathrm{t}-\alpha )}\mathrm{dt}$$$${=}_{\xi \mathrm{t}=\mathrm{u}}\int \frac{\mathrm{u}}{\xi (1+{\mathrm{u}}^2)(\alpha \frac{{\mathrm{u}}^2}{{\xi }^2}-2\beta \frac{\mathrm{u}}{\xi }-\alpha )}\frac{\mathrm{du}}{\xi }$$$$=\int \frac{\mathrm{udu}}{{\xi }^2({\mathrm{u}}^2+1)(\alpha \frac{{\mathrm{u}}^2}{{\xi }^2}-2\beta \frac{\mathrm{u}}{\xi }-\alpha )}=\int \frac{\mathrm{udu}}{({\mathrm{u}}^2+1)(\alpha {\mathrm{u}}^2-2\beta \xi \mathrm{u}-\alpha {\xi }^2)}$$$$\mathrm{let}\mathrm{decompose}\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{u}}{({\mathrm{u}}^2+1)(\alpha {\mathrm{u}}^2-2\beta \xi \mathrm{u}-\alpha {\xi }^2)}$$$$\alpha {\mathrm{u}}^2-2\beta \xi \mathrm{u}-\alpha {\xi }^2\to {\mathrm{\Delta }}^{{}^{\prime }}={\beta }^2{\xi }^2-{\alpha }^2{\xi }^2={\xi }^2({\beta }^2-{\alpha }^2)={\xi }^2({\mathrm{b}}^4-{\mathrm{a}}^4)$$$$\mathrm{case}1\mid \mathrm{b}\mid >\mid \mathrm{a}\mid \Rightarrow {\mathrm{u}}_1=\frac{\beta \xi +\xi \sqrt{{\beta }^2-{\alpha }^2}}{\alpha }\mathrm{and}{\mathrm{u}}_2=\frac{\beta \xi -\xi \sqrt{{\beta }^2-{\alpha }^2}}{\alpha }\Rightarrow$$$$\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{u}}{({\mathrm{u}}^2+1)\alpha (\mathrm{u}-{\mathrm{u}}_1)(\mathrm{u}-{\mathrm{u}}_2)}=\frac{{\mathrm{a}}_1}{\mathrm{u}-{\mathrm{u}}_1}+\frac{{\mathrm{a}}_2}{\mathrm{u}-{\mathrm{u}}_2}+\frac{{\mathrm{b}}_1\mathrm{u}+{\mathrm{b}}_2}{{\mathrm{u}}^2+1}$$$$\mathrm{eazy}\mathrm{to}\mathrm{find}{\mathrm{a}}_{\mathrm{i}}\mathrm{and}{\mathrm{b}}_{\mathrm{i}}\Rightarrow$$$${\mathrm{f}}^{{}^{\prime }}\left(\xi \right)={\mathrm{a}}_1\ln \mid \mathrm{u}-{\mathrm{u}}_1\mid +{\mathrm{a}}_2\ln \mid \mathrm{u}-{\mathrm{u}}_2\mid +\frac{{\mathrm{b}}_1}{2}\ln ({\mathrm{u}}^2+1)+{\mathrm{b}}_2\arctan \left(\mathrm{u}\right)+\mathrm{c}\Rightarrow$$$$\mathrm{f}\left(\xi \right)={\mathrm{a}}_1\int \ln \mid \mathrm{u}-{\mathrm{u}}_1\mid \mathrm{d}\xi +{\mathrm{a}}_2\int \ln \mid \mathrm{u}-{\mathrm{u}}_2\mid \mathrm{d}\xi +\frac{{\mathrm{b}}_1}{2}\int \ln \mid {\mathrm{u}}^2+1\mid \mathrm{d}\xi +{\mathrm{b}}_2\int \mathrm{arctanu}\mathrm{d}\xi +\mathrm{c}\xi$$$$...\mathrm{be}\mathrm{continued}...$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com