
Question Number 103560 by abony1303 last updated on 15/Jul/20
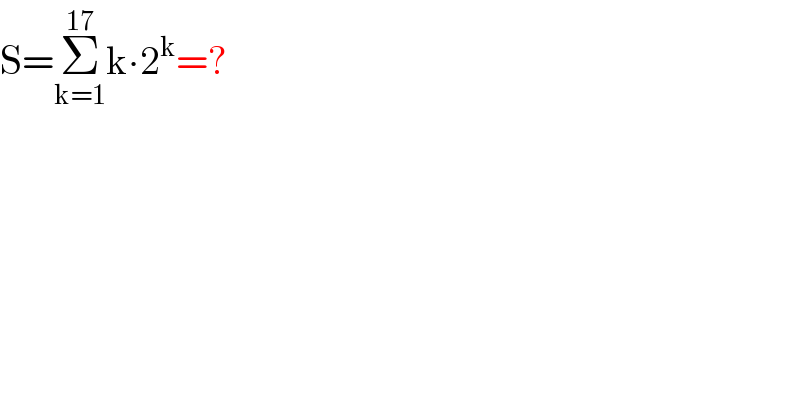
$$\mathrm{S}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{17}} {\sum}}\mathrm{k}\centerdot\mathrm{2}^{\mathrm{k}} =? \\ $$
Commented by abony1303 last updated on 15/Jul/20

$$\mathrm{pls}\:\mathrm{help} \\ $$
Answered by mr W last updated on 15/Jul/20
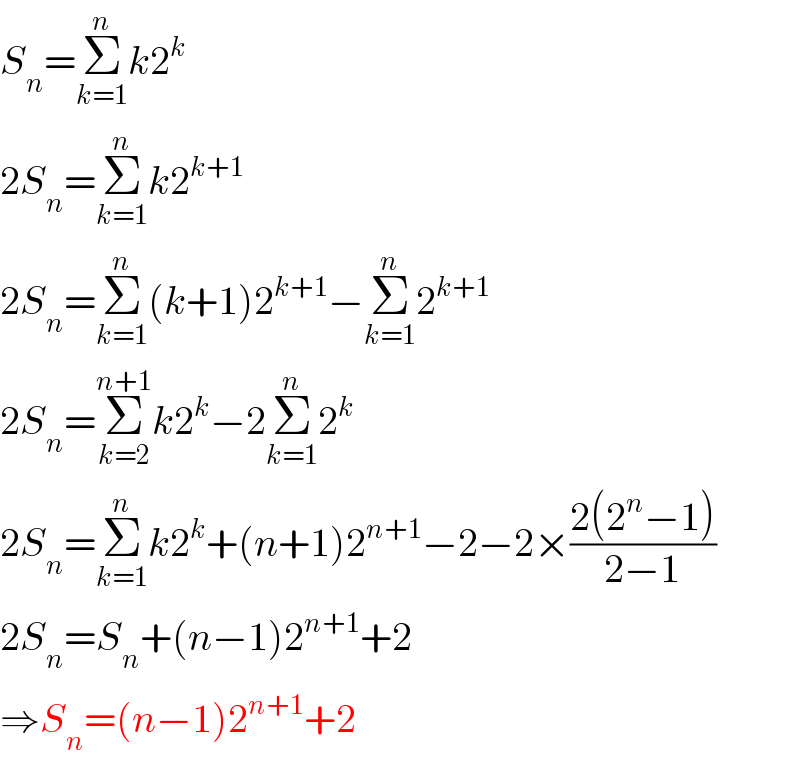
$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}} \\ $$$$\mathrm{2}{S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}+\mathrm{1}} \\ $$$$\mathrm{2}{S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}\right)\mathrm{2}^{{k}+\mathrm{1}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}+\mathrm{1}} \\ $$$$\mathrm{2}{S}_{{n}} =\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{k}\mathrm{2}^{{k}} −\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \\ $$$$\mathrm{2}{S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}} +\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{2}−\mathrm{2}×\frac{\mathrm{2}\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}−\mathrm{1}} \\ $$$$\mathrm{2}{S}_{{n}} ={S}_{{n}} +\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{2} \\ $$$$\Rightarrow{S}_{{n}} =\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{2} \\ $$
Answered by Dwaipayan Shikari last updated on 15/Jul/20

$${S}_{{n}} =\mathrm{1}.\mathrm{2}+\mathrm{2}.\mathrm{2}^{\mathrm{2}} +\mathrm{3}.\mathrm{2}^{\mathrm{3}} +...........+{n}.\mathrm{2}^{{n}} \\ $$$$ \\ $$$$\mathrm{2}{S}_{{n}} =\mathrm{1}.\mathrm{2}^{\mathrm{2}} +\mathrm{2}.\mathrm{2}^{\mathrm{3}} +.....+\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}} +{n}\mathrm{2}^{{n}+\mathrm{1}} \\ $$$$............{Subtracting} \\ $$$$−{S}_{{n}} =\mathrm{1}.\mathrm{2}+\mathrm{1}.\mathrm{2}^{\mathrm{2}} +\mathrm{1}.\mathrm{2}^{\mathrm{3}} +....+\mathrm{2}^{{n}} −{n}\mathrm{2}^{{n}+\mathrm{1}} \\ $$$${S}_{{n}} ={n}\mathrm{2}^{{n}+\mathrm{1}} −\left(\mathrm{1}.\mathrm{2}+\frac{\mathrm{2}^{{n}} −\mathrm{1}}{\mathrm{1}}\right) \\ $$$${S}_{{n}} =\left({n}−\mathrm{1}\right)^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{2} \\ $$$${S}_{\mathrm{17}} =\mathrm{16}.\mathrm{2}^{\mathrm{18}} +\mathrm{2}\:\:\left(\circledast\blacksquare\bigstar\:\:\mathrm{DS}\right) \\ $$
Answered by OlafThorendsen last updated on 15/Jul/20
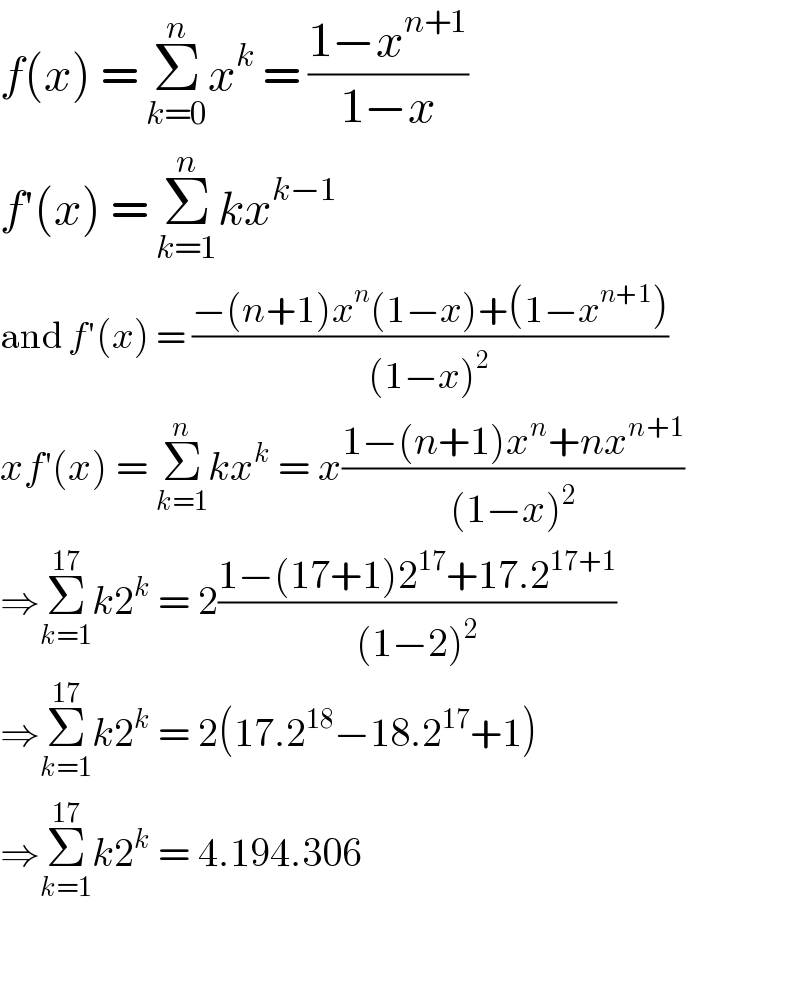
$${f}\left({x}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{k}} \:=\:\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}} \\ $$$${f}'\left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{kx}^{{k}−\mathrm{1}} \\ $$$$\mathrm{and}\:{f}'\left({x}\right)\:=\:\frac{−\left({n}+\mathrm{1}\right){x}^{{n}} \left(\mathrm{1}−{x}\right)+\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${xf}'\left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{kx}^{{k}} \:=\:{x}\frac{\mathrm{1}−\left({n}+\mathrm{1}\right){x}^{{n}} +{nx}^{{n}+\mathrm{1}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\mathrm{17}} {\sum}}{k}\mathrm{2}^{{k}} \:=\:\mathrm{2}\frac{\mathrm{1}−\left(\mathrm{17}+\mathrm{1}\right)\mathrm{2}^{\mathrm{17}} +\mathrm{17}.\mathrm{2}^{\mathrm{17}+\mathrm{1}} }{\left(\mathrm{1}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\mathrm{17}} {\sum}}{k}\mathrm{2}^{{k}} \:=\:\mathrm{2}\left(\mathrm{17}.\mathrm{2}^{\mathrm{18}} −\mathrm{18}.\mathrm{2}^{\mathrm{17}} +\mathrm{1}\right) \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\mathrm{17}} {\sum}}{k}\mathrm{2}^{{k}} \:=\:\mathrm{4}.\mathrm{194}.\mathrm{306} \\ $$$$ \\ $$
