Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 103563 by mohammad17 last updated on 15/Jul/20

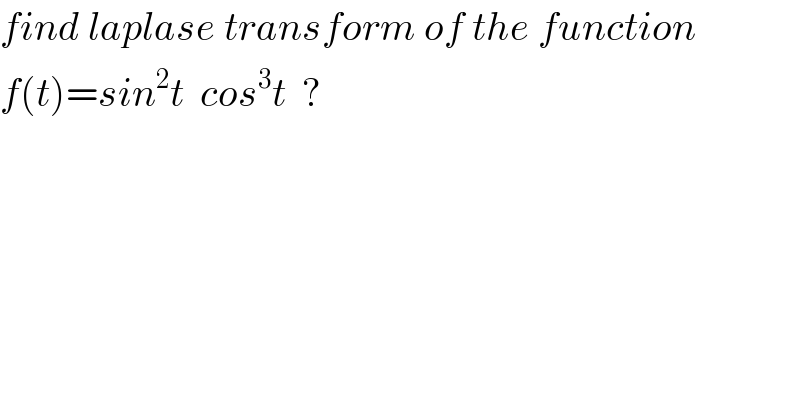
find laplase transform of the function f(t)=sin^2 t cos^3 t ?

$${find}\:{laplase}\:{transform}\:{of}\:{the}\:{function} \\ $$$${f}\left({t}\right)={sin}^{\mathrm{2}} {t}\:\:{cos}^{\mathrm{3}} {t}\:\:? \\ $$

Answered by MAB last updated on 15/Jul/20

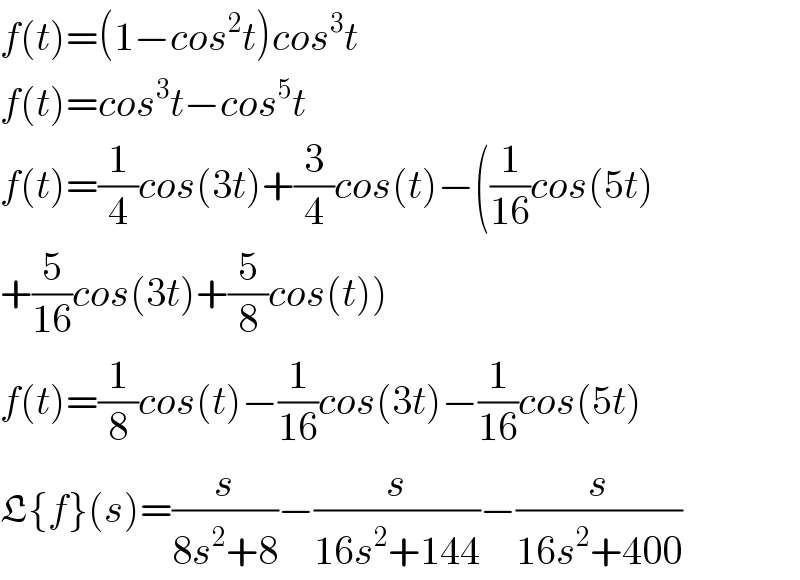
f(t)=(1−cos^2 t)cos^3 t f(t)=cos^3 t−cos^5 t f(t)=(1/4)cos(3t)+(3/4)cos(t)−((1/(16))cos(5t) +(5/(16))cos(3t)+(5/8)cos(t)) f(t)=(1/8)cos(t)−(1/(16))cos(3t)−(1/(16))cos(5t) L{f}(s)=(s/(8s^2 +8))−(s/(16s^2 +144))−(s/(16s^2 +400))

$${f}\left({t}\right)=\left(\mathrm{1}−{cos}^{\mathrm{2}} {t}\right){cos}^{\mathrm{3}} {t} \\ $$$${f}\left({t}\right)={cos}^{\mathrm{3}} {t}−{cos}^{\mathrm{5}} {t} \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{3}{t}\right)+\frac{\mathrm{3}}{\mathrm{4}}{cos}\left({t}\right)−\left(\frac{\mathrm{1}}{\mathrm{16}}{cos}\left(\mathrm{5}{t}\right)\right. \\ $$$$\left.+\frac{\mathrm{5}}{\mathrm{16}}{cos}\left(\mathrm{3}{t}\right)+\frac{\mathrm{5}}{\mathrm{8}}{cos}\left({t}\right)\right) \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{8}}{cos}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{16}}{cos}\left(\mathrm{3}{t}\right)−\frac{\mathrm{1}}{\mathrm{16}}{cos}\left(\mathrm{5}{t}\right) \\ $$$$\mathfrak{L}\left\{{f}\right\}\left({s}\right)=\frac{{s}}{\mathrm{8}{s}^{\mathrm{2}} +\mathrm{8}}−\frac{{s}}{\mathrm{16}{s}^{\mathrm{2}} +\mathrm{144}}−\frac{{s}}{\mathrm{16}{s}^{\mathrm{2}} +\mathrm{400}} \\ $$

Answered by mathmax by abdo last updated on 16/Jul/20

f(t)=sin^2 t cos^3 t ⇒f(t) =sin^2 t .cos^2 t cost =((1/2)sin(2t))^2 cost =(1/4) sin^2 (2t)cost =(1/4)(((1−cos(4t))/2))cost =(1/8)cost−(1/8)cost cos(4t) =(1/8)cost−(1/(16)){ cos(5t)+cos(3t)} ⇒L(f(t))=(1/8)L(cost)−(1/(16))L(cos(5t)) −(1/(16))L(cos(3t)) but L(cos(wt))=∫_0 ^∞ cos(wx)e^(−tx) dt =Re(∫_0 ^∞ e^(iwx−tx) dt and ∫_0 ^∞ e^((−t+iw)x) dx =[(1/(−t+iw))e^((−t+iw)x) ]_0 ^∞ =((−1)/(−t+iw)) =(1/(t−iw)) =((t+iw)/(t^2 +w^2 )) ⇒ L(cos(wt)) =(t/(t^2 +w^2 )) ⇒ L(f(t)) =(t/(8(t^2 +1)))−(1/6)×(t/(t^2 +25))−(1/(16))×(t/(t^2 +9))

$$\mathrm{f}\left(\mathrm{t}\right)=\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:\mathrm{cos}^{\mathrm{3}} \mathrm{t}\:\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)\:=\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:.\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{cost} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2t}\right)\right)^{\mathrm{2}} \mathrm{cost}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2t}\right)\mathrm{cost} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4t}\right)}{\mathrm{2}}\right)\mathrm{cost}\:=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cost}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cost}\:\mathrm{cos}\left(\mathrm{4t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cost}−\frac{\mathrm{1}}{\mathrm{16}}\left\{\:\mathrm{cos}\left(\mathrm{5t}\right)+\mathrm{cos}\left(\mathrm{3t}\right)\right\}\:\Rightarrow\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{L}\left(\mathrm{cost}\right)−\frac{\mathrm{1}}{\mathrm{16}}\mathrm{L}\left(\mathrm{cos}\left(\mathrm{5t}\right)\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{16}}\mathrm{L}\left(\mathrm{cos}\left(\mathrm{3t}\right)\right) \\ $$$$\mathrm{but}\:\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{wx}\right)\mathrm{e}^{−\mathrm{tx}} \mathrm{dt}\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\mathrm{iwx}−\mathrm{tx}} \mathrm{dt}\:\mathrm{and}\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\left(−\mathrm{t}+\mathrm{iw}\right)\mathrm{x}} \mathrm{dx}\:=\left[\frac{\mathrm{1}}{−\mathrm{t}+\mathrm{iw}}\mathrm{e}^{\left(−\mathrm{t}+\mathrm{iw}\right)\mathrm{x}} \right]_{\mathrm{0}} ^{\infty} \:=\frac{−\mathrm{1}}{−\mathrm{t}+\mathrm{iw}}\:=\frac{\mathrm{1}}{\mathrm{t}−\mathrm{iw}}\:=\frac{\mathrm{t}+\mathrm{iw}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)\:=\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\frac{\mathrm{t}}{\mathrm{8}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{25}}−\frac{\mathrm{1}}{\mathrm{16}}×\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}} \\ $$

Commented by mathmax by abdo last updated on 16/Jul/20

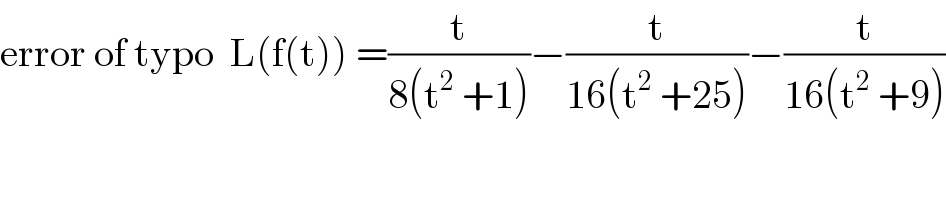
error of typo L(f(t)) =(t/(8(t^2 +1)))−(t/(16(t^2 +25)))−(t/(16(t^2 +9)))

$$\mathrm{error}\:\mathrm{of}\:\mathrm{typo}\:\:\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\frac{\mathrm{t}}{\mathrm{8}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}−\frac{\mathrm{t}}{\mathrm{16}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{25}\right)}−\frac{\mathrm{t}}{\mathrm{16}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com