Question Number 103607 by bemath last updated on 16/Jul/20

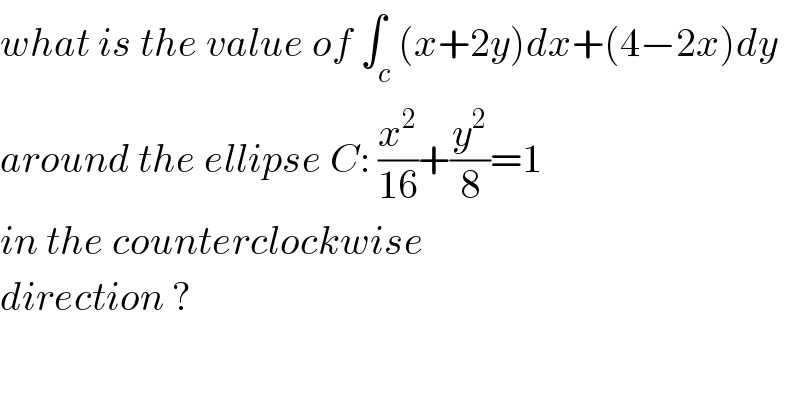
what is the value of ∫_c (x+2y)dx+(4−2x)dy around the ellipse C: (x^2 /(16))+(y^2 /8)=1 in the counterclockwise direction ?

Answered by bobhans last updated on 16/Jul/20

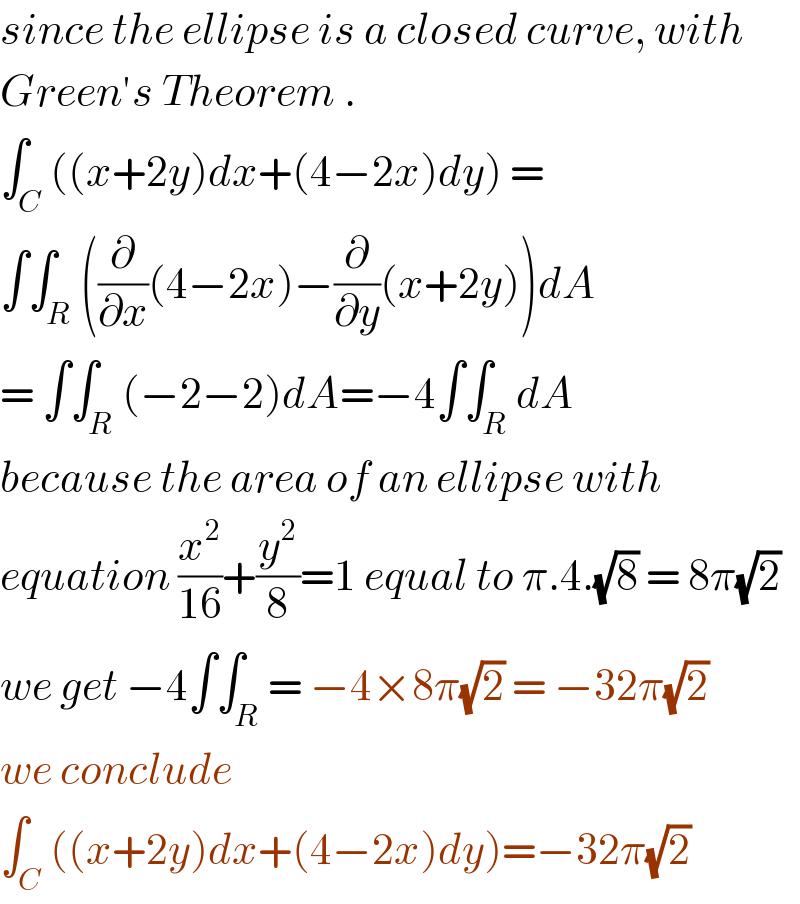
since the ellipse is a closed curve, with Green′s Theorem . ∫_C ((x+2y)dx+(4−2x)dy) = ∫∫_R ((∂/∂x)(4−2x)−(∂/∂y)(x+2y))dA = ∫∫_R (−2−2)dA=−4∫∫_R dA because the area of an ellipse with equation (x^2 /(16))+(y^2 /8)=1 equal to π.4.(√8) = 8π(√2) we get −4∫∫_R = −4×8π(√2) = −32π(√2) we conclude ∫_C ((x+2y)dx+(4−2x)dy)=−32π(√2)