Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 103622 by bobhans last updated on 16/Jul/20

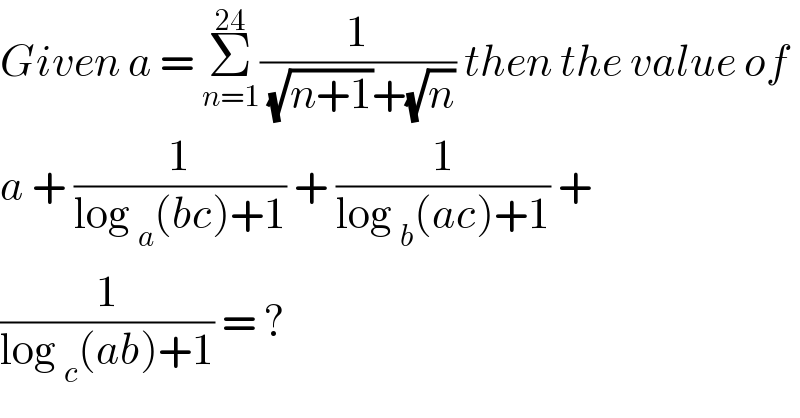
Given a = Σ_(n=1) ^(24) (1/((√(n+1))+(√n))) then the value of a + (1/(log _a (bc)+1)) + (1/(log _b (ac)+1)) + (1/(log _c (ab)+1)) = ?

$${Given}\:{a}\:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{24}} {\sum}}\frac{\mathrm{1}}{\sqrt{{n}+\mathrm{1}}+\sqrt{{n}}}\:{then}\:{the}\:{value}\:{of} \\ $$$${a}\:+\:\frac{\mathrm{1}}{\mathrm{log}\:_{{a}} \left({bc}\right)+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{log}\:_{{b}} \left({ac}\right)+\mathrm{1}}\:+ \\ $$$$\frac{\mathrm{1}}{\mathrm{log}\:_{{c}} \left({ab}\right)+\mathrm{1}}\:=\:? \\ $$

Answered by OlafThorendsen last updated on 16/Jul/20

(1/((√(n+1))+(√n))) = (√(n+1))−(√n) Then a = Σ_(n=1) ^(24) ((√(n+1))−(√n)) = (√(25)) = 5 5+(1/(log_5 (bc)+1))+(1/(log_b (5c)+1))+(1/(log_c (5b)+1)) 5+(1/(((ln(bc))/(ln5))+1))+(1/(((ln(5c))/(lnb))+1))+(1/(((ln(5b))/(lnc))+1)) 5+((ln5)/(ln(bc)+ln5))+((lnb)/(ln(5c)+lnb))+((lnc)/(ln(5b)+lnc)) 5+((ln5)/(ln(5bc)))+((lnb)/(ln(5bc)))+((lnc)/(ln(5bc))) 5+((ln(5bc))/(ln(5bc))) = 5+1 = 6

$$\frac{\mathrm{1}}{\sqrt{{n}+\mathrm{1}}+\sqrt{{n}}}\:=\:\sqrt{{n}+\mathrm{1}}−\sqrt{{n}} \\ $$$$\mathrm{Then}\:{a}\:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{24}} {\sum}}\left(\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}\right)\:=\:\sqrt{\mathrm{25}}\:=\:\mathrm{5} \\ $$$$\mathrm{5}+\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{5}} \left({bc}\right)+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{log}_{{b}} \left(\mathrm{5}{c}\right)+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{log}_{{c}} \left(\mathrm{5}{b}\right)+\mathrm{1}} \\ $$$$\mathrm{5}+\frac{\mathrm{1}}{\frac{\mathrm{ln}\left({bc}\right)}{\mathrm{ln5}}+\mathrm{1}}+\frac{\mathrm{1}}{\frac{\mathrm{ln}\left(\mathrm{5}{c}\right)}{\mathrm{ln}{b}}+\mathrm{1}}+\frac{\mathrm{1}}{\frac{\mathrm{ln}\left(\mathrm{5}{b}\right)}{\mathrm{ln}{c}}+\mathrm{1}} \\ $$$$\mathrm{5}+\frac{\mathrm{ln5}}{\mathrm{ln}\left({bc}\right)+\mathrm{ln5}}+\frac{\mathrm{ln}{b}}{\mathrm{ln}\left(\mathrm{5}{c}\right)+\mathrm{ln}{b}}+\frac{\mathrm{ln}{c}}{\mathrm{ln}\left(\mathrm{5}{b}\right)+\mathrm{ln}{c}} \\ $$$$\mathrm{5}+\frac{\mathrm{ln5}}{\mathrm{ln}\left(\mathrm{5}{bc}\right)}+\frac{\mathrm{ln}{b}}{\mathrm{ln}\left(\mathrm{5}{bc}\right)}+\frac{\mathrm{ln}{c}}{\mathrm{ln}\left(\mathrm{5}{bc}\right)} \\ $$$$\mathrm{5}+\frac{\mathrm{ln}\left(\mathrm{5}{bc}\right)}{\mathrm{ln}\left(\mathrm{5}{bc}\right)}\:=\:\mathrm{5}+\mathrm{1}\:=\:\mathrm{6} \\ $$$$ \\ $$

Commented by bobhans last updated on 16/Jul/20

cooll

$${cooll} \\ $$

Commented by bemath last updated on 16/Jul/20

wrong sir Σ_(n=1) ^(24) (√(n+1))−(√n) = 4

$${wrong}\:{sir}\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{24}} {\sum}}\:\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}\:=\:\mathrm{4}\: \\ $$

Commented by OlafThorendsen last updated on 16/Jul/20

exact sir. you are right.

$$\mathrm{exact}\:\mathrm{sir}.\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}. \\ $$

Answered by bemath last updated on 16/Jul/20

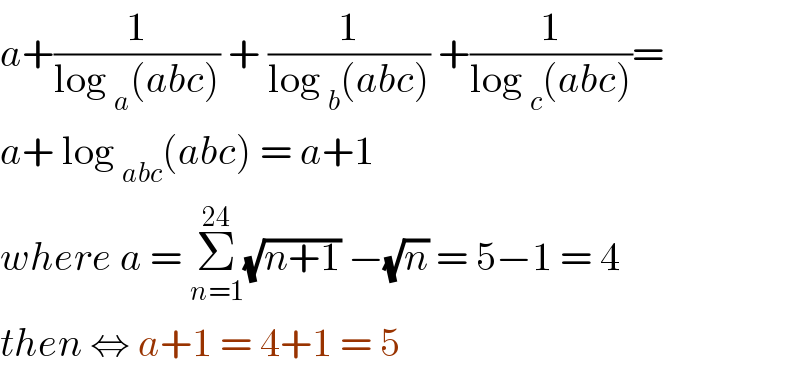
a+(1/(log _a (abc))) + (1/(log _b (abc))) +(1/(log _c (abc)))= a+ log _(abc) (abc) = a+1 where a = Σ_(n=1) ^(24) (√(n+1)) −(√n) = 5−1 = 4 then ⇔ a+1 = 4+1 = 5

$${a}+\frac{\mathrm{1}}{\mathrm{log}\:_{{a}} \left({abc}\right)}\:+\:\frac{\mathrm{1}}{\mathrm{log}\:_{{b}} \left({abc}\right)}\:+\frac{\mathrm{1}}{\mathrm{log}\:_{{c}} \left({abc}\right)}= \\ $$$${a}+\:\mathrm{log}\:_{{abc}} \left({abc}\right)\:=\:{a}+\mathrm{1}\: \\ $$$${where}\:{a}\:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{24}} {\sum}}\sqrt{{n}+\mathrm{1}}\:−\sqrt{{n}}\:=\:\mathrm{5}−\mathrm{1}\:=\:\mathrm{4} \\ $$$${then}\:\Leftrightarrow\:{a}+\mathrm{1}\:=\:\mathrm{4}+\mathrm{1}\:=\:\mathrm{5}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com