Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 103623 by Lordose last updated on 16/Jul/20

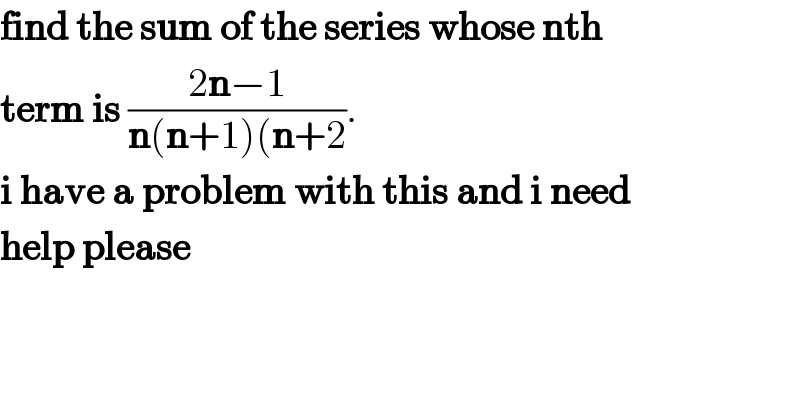
find the sum of the series whose nth term is ((2n−1)/(n(n+1)(n+2)). i have a problem with this and i need help please

$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{series}}\:\boldsymbol{\mathrm{whose}}\:\boldsymbol{\mathrm{nth}} \\ $$$$\boldsymbol{\mathrm{term}}\:\boldsymbol{\mathrm{is}}\:\frac{\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}}{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}+\mathrm{2}\right.}. \\ $$$$\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{problem}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{need}} \\ $$$$\boldsymbol{\mathrm{help}}\:\boldsymbol{\mathrm{please}} \\ $$

Answered by OlafThorendsen last updated on 16/Jul/20

find the sum of the series whose nth term is ((2n−1)/(n(n+1)(n+2)). i have a problem with this and i need help please u_n = ((2n−1)/(n(n+1)(n+2))) u_n = −(1/2).(1/n)+(3/(n+1))−(5/2).(1/(n+2)) Σ_(n=1) ^p u_n = −(1/2)Σ_(n=1) ^p (1/n)+3Σ_(n=1) ^p (1/(n+1))−(5/2)Σ_(n=1) ^p (1/(n+2)) Σ_(n=1) ^p u_n = −(1/2)Σ_(n=1) ^p (1/n)+3Σ_(n=2) ^(p+1) (1/n)−(5/2)Σ_(n=3) ^(p+2) (1/n) Σ_(n=1) ^p u_n = −(1/2)(1+(1/2))+3((1/2))+3((1/(p+1)))−(5/2)((1/(p+1))+(1/(p+2))) Σ_(n=1) ^p u_n = (3/4)+(1/2)((1/(p+1)))−(5/2)((1/(p+2))) Σ_(n=1) ^p u_n = (3/4)−((2p+(3/2))/((p+1)(p+2))) and Σ_(n=1) ^∞ u_n = (3/4)

$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{series}}\:\boldsymbol{\mathrm{whose}}\:\boldsymbol{\mathrm{nth}} \\ $$$$\boldsymbol{\mathrm{term}}\:\boldsymbol{\mathrm{is}}\:\frac{\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}}{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}+\mathrm{2}\right.}. \\ $$$$\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{problem}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{need}} \\ $$$$\boldsymbol{\mathrm{help}}\:\boldsymbol{\mathrm{please}} \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{2}{n}−\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$${u}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{{n}}+\frac{\mathrm{3}}{{n}+\mathrm{1}}−\frac{\mathrm{5}}{\mathrm{2}}.\frac{\mathrm{1}}{{n}+\mathrm{2}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}{u}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\frac{\mathrm{1}}{{n}}+\mathrm{3}\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{5}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{2}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}{u}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\frac{\mathrm{1}}{{n}}+\mathrm{3}\underset{{n}=\mathrm{2}} {\overset{{p}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{5}}{\mathrm{2}}\underset{{n}=\mathrm{3}} {\overset{{p}+\mathrm{2}} {\sum}}\frac{\mathrm{1}}{{n}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}{u}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3}\left(\frac{\mathrm{1}}{{p}+\mathrm{1}}\right)−\frac{\mathrm{5}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{p}+\mathrm{1}}+\frac{\mathrm{1}}{{p}+\mathrm{2}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}{u}_{{n}} \:=\:\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{p}+\mathrm{1}}\right)−\frac{\mathrm{5}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{p}+\mathrm{2}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}{u}_{{n}} \:=\:\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{2}{p}+\frac{\mathrm{3}}{\mathrm{2}}}{\left({p}+\mathrm{1}\right)\left({p}+\mathrm{2}\right)} \\ $$$$\mathrm{and}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}} \:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$

Commented by Lordose last updated on 16/Jul/20

sir i don′t understand the 4th line can you explain pls

$$\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{don}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{understand}}\:\boldsymbol{\mathrm{the}}\:\mathrm{4}\boldsymbol{\mathrm{th}}\:\boldsymbol{\mathrm{line}} \\ $$$$\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{explain}}\:\boldsymbol{\mathrm{pls}} \\ $$

Answered by bobhans last updated on 16/Jul/20

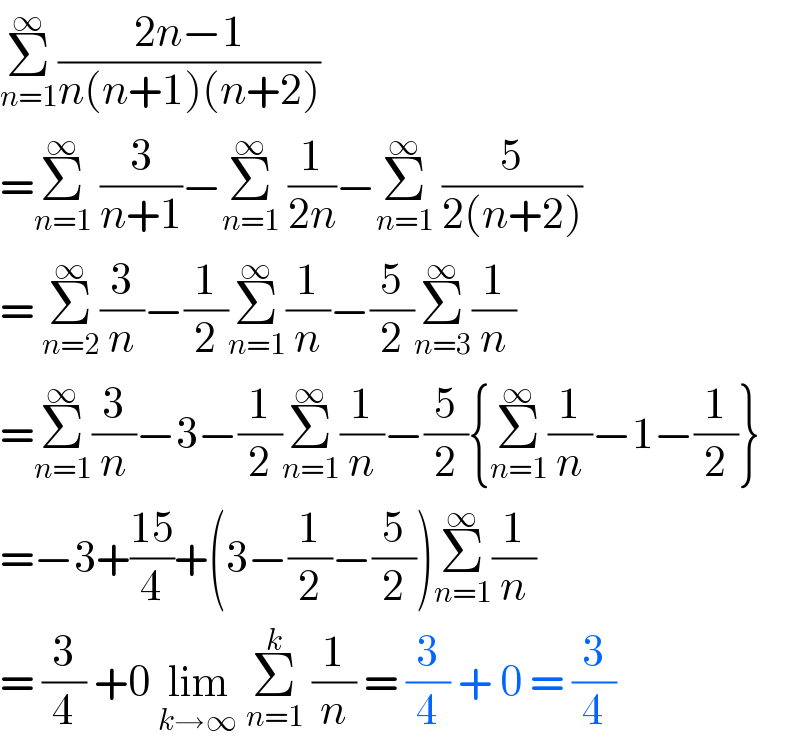
Σ_(n=1) ^∞ ((2n−1)/(n(n+1)(n+2))) =Σ_(n=1) ^∞ (3/(n+1))−Σ_(n=1) ^∞ (1/(2n))−Σ_(n=1) ^∞ (5/(2(n+2))) = Σ_(n=2) ^∞ (3/n)−(1/2)Σ_(n=1) ^∞ (1/n)−(5/2)Σ_(n=3) ^∞ (1/n) =Σ_(n=1) ^∞ (3/n)−3−(1/2)Σ_(n=1) ^∞ (1/n)−(5/2){Σ_(n=1) ^∞ (1/n)−1−(1/2)} =−3+((15)/4)+(3−(1/2)−(5/2))Σ_(n=1) ^∞ (1/n) = (3/4) +0 lim_(k→∞) Σ_(n=1) ^k (1/n) = (3/4) + 0 = (3/4)

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}−\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{3}}{{n}+\mathrm{1}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}{n}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{5}}{\mathrm{2}\left({n}+\mathrm{2}\right)} \\ $$$$=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{3}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{5}}{\mathrm{2}}\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}}{{n}}−\mathrm{3}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{5}}{\mathrm{2}}\left\{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right\} \\ $$$$=−\mathrm{3}+\frac{\mathrm{15}}{\mathrm{4}}+\left(\mathrm{3}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{2}}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{4}}\:+\mathrm{0}\:\underset{{k}\rightarrow\infty} {\mathrm{lim}}\:\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\:\frac{\mathrm{1}}{{n}}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\mathrm{0}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Commented by Lordose last updated on 16/Jul/20

can anyone make me understand pls

$$\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{anyone}}\:\boldsymbol{\mathrm{make}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{understand}}\:\boldsymbol{\mathrm{pls}} \\ $$

Commented by bobhans last updated on 16/Jul/20

what part you don′t understand?

$${what}\:{part}\:{you}\:{don}'{t}\:{understand}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com