
Question Number 103644 by dw last updated on 16/Jul/20

Commented by dw last updated on 16/Jul/20
![[Trigonometric Substit.]](Q103646.png)
$$\left[{Trigonometric}\:{Substit}.\right] \\ $$
Answered by 1549442205 last updated on 16/Jul/20
![putting x=cosϕ(ϕ∈[0,π])we have ((5cosϕ)/(sinϕ))−6cosϕsinϕ=2⇔5cosϕ−6cosϕsin^2 ϕ=2sinϕ Putting tan(ϕ/2)=t we get ((5(1−t^2 ))/(1+t^2 ))−((6(1−t^2 )4t^2 )/((1+t^2 )^3 ))=((4t)/(1+t^2 )) 5(1−t^4 )(1+t^2 )−24(t^2 −t^4 )=4t(t^4 +2t^2 +1) −5t^6 −5t^4 +5t^2 +5−24t^2 +24t^4 =4t^5 +8t^3 +4t ⇔5t^6 +4t^5 −19t^4 +8t^3 +19t^2 +4t−5=0 ⇔5(t^3 −(1/t^3 ))+4(t^2 +(1/t^2 ))−19(t−(1/t))+8=0(1) Putting (t−(1/t))=y⇒t^3 −(1/t^3 )−3(t−(1/t))=y^3 t^2 +(1/t^2 )=y^2 +2.Hence, (1)⇔5y^3 +4y^2 +8−4y+8=0 ⇔5y^3 +4y^2 −4y+16=0 ⇔(y+2)(5y^2 −6y+8)=0 ⇔y+2=0 (because 5y^2 −6y+8=y^2 +(2y−(3/2))^2 +((23)/4)>0) ⇔y=−2⇔t−(1/t)=−2⇔t^2 +2t−1=0 ⇔t=−1±(√2) i)For t=−1+(√2) ⇒t^2 =3−2(√2) we get x=cosϕ=((1−t^2 )/(1+t^2 ))=((2(√2)−2)/(4−2(√2)))=(((√2)−1)/(2−(√2)))=(1/(√2)) ii)For t=−1−(√2) ⇒t^2 =3+2(√2) we get x=cosϕ=((1−t^2 )/(1+t^2 ))=((−2(1+(√2)))/(2(2+(√(2)))))=((−1)/(√2)) Thus ,x∈{−(1/2);((√2)/(√2))} second way: ((5x)/(√(1−x^2 )))+6x(√(1−x^2 ))=2⇔5x−6x(1−x^2 )=2(√(1−x^2 )) ⇔(6x^3 −x)^2 =4(1−x^2 ) ⇔36x^6 −12x^4 +x^2 =4−4x^2 Putting x^2 =y we get 36y^3 −12y^2 +5y−4=0 ⇔(2y−1)(18y^2 −3y+4)=0 ⇔2y−1=0 because 18y^2 −3y+4=17y^2 +(y−(3/2))^2 +(7/4)>0 ⇔y=(1/2)⇔x^2 =(1/2)⇔x=±((√2)/2)](Q103657.png)
$$\mathrm{putting}\:\mathrm{x}=\mathrm{cos}\varphi\left(\varphi\in\left[\mathrm{0},\pi\right]\right)\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{5cos}\varphi}{\mathrm{sin}\varphi}−\mathrm{6cos}\varphi\mathrm{sin}\varphi=\mathrm{2}\Leftrightarrow\mathrm{5cos}\varphi−\mathrm{6cos}\varphi\mathrm{sin}^{\mathrm{2}} \varphi=\mathrm{2sin}\varphi \\ $$$$\mathrm{Putting}\:\mathrm{tan}\frac{\varphi}{\mathrm{2}}=\mathrm{t}\:\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{5}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{6}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{4t}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{\mathrm{4t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{5}\left(\mathrm{1}−\mathrm{t}^{\mathrm{4}} \right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)−\mathrm{24}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}^{\mathrm{4}} \right)=\mathrm{4t}\left(\mathrm{t}^{\mathrm{4}} +\mathrm{2t}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$−\mathrm{5t}^{\mathrm{6}} −\mathrm{5t}^{\mathrm{4}} +\mathrm{5t}^{\mathrm{2}} +\mathrm{5}−\mathrm{24t}^{\mathrm{2}} +\mathrm{24t}^{\mathrm{4}} =\mathrm{4t}^{\mathrm{5}} +\mathrm{8t}^{\mathrm{3}} +\mathrm{4t} \\ $$$$\Leftrightarrow\mathrm{5t}^{\mathrm{6}} +\mathrm{4t}^{\mathrm{5}} −\mathrm{19t}^{\mathrm{4}} +\mathrm{8t}^{\mathrm{3}} +\mathrm{19t}^{\mathrm{2}} +\mathrm{4t}−\mathrm{5}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{5}\left(\mathrm{t}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\right)+\mathrm{4}\left(\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)−\mathrm{19}\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)+\mathrm{8}=\mathrm{0}\left(\mathrm{1}\right) \\ $$$$\mathrm{Putting}\:\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)=\mathrm{y}\Rightarrow\mathrm{t}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }−\mathrm{3}\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)=\mathrm{y}^{\mathrm{3}} \\ $$$$\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }=\mathrm{y}^{\mathrm{2}} +\mathrm{2}.\mathrm{Hence}, \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{5y}^{\mathrm{3}} +\mathrm{4y}^{\mathrm{2}} +\mathrm{8}−\mathrm{4y}+\mathrm{8}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{5y}^{\mathrm{3}} +\mathrm{4y}^{\mathrm{2}} −\mathrm{4y}+\mathrm{16}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{y}+\mathrm{2}\right)\left(\mathrm{5y}^{\mathrm{2}} −\mathrm{6y}+\mathrm{8}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{y}+\mathrm{2}=\mathrm{0}\:\left(\mathrm{because}\:\mathrm{5y}^{\mathrm{2}} −\mathrm{6y}+\mathrm{8}=\mathrm{y}^{\mathrm{2}} +\left(\mathrm{2y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{23}}{\mathrm{4}}>\mathrm{0}\right) \\ $$$$\Leftrightarrow\mathrm{y}=−\mathrm{2}\Leftrightarrow\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}=−\mathrm{2}\Leftrightarrow\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{t}=−\mathrm{1}\pm\sqrt{\mathrm{2}} \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{t}=−\mathrm{1}+\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{t}^{\mathrm{2}} =\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}=\mathrm{cos}\varphi=\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\left.\mathrm{ii}\right)\mathrm{For}\:\mathrm{t}=−\mathrm{1}−\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{t}^{\mathrm{2}} =\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}=\mathrm{cos}\varphi=\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\frac{−\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}\left(\mathrm{2}+\sqrt{\left.\mathrm{2}\right)}\right.}=\frac{−\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\boldsymbol{\mathrm{Thus}}\:,\boldsymbol{\mathrm{x}}\in\left\{−\frac{\mathrm{1}}{\mathrm{2}};\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}}\right\} \\ $$$$\boldsymbol{\mathrm{second}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\frac{\mathrm{5x}}{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}+\mathrm{6x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }=\mathrm{2}\Leftrightarrow\mathrm{5x}−\mathrm{6x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)=\mathrm{2}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\left(\mathrm{6x}^{\mathrm{3}} −\mathrm{x}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\mathrm{36x}^{\mathrm{6}} −\mathrm{12x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} =\mathrm{4}−\mathrm{4x}^{\mathrm{2}} \\ $$$$\mathrm{Putting}\:\mathrm{x}^{\mathrm{2}} =\mathrm{y}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{36y}^{\mathrm{3}} −\mathrm{12y}^{\mathrm{2}} +\mathrm{5y}−\mathrm{4}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{2y}−\mathrm{1}\right)\left(\mathrm{18y}^{\mathrm{2}} −\mathrm{3y}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2y}−\mathrm{1}=\mathrm{0}\:\mathrm{because}\:\mathrm{18y}^{\mathrm{2}} −\mathrm{3y}+\mathrm{4}=\mathrm{17y}^{\mathrm{2}} +\left(\mathrm{y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{4}}>\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}}\Leftrightarrow\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\Leftrightarrow\boldsymbol{\mathrm{x}}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by maths mind last updated on 16/Jul/20
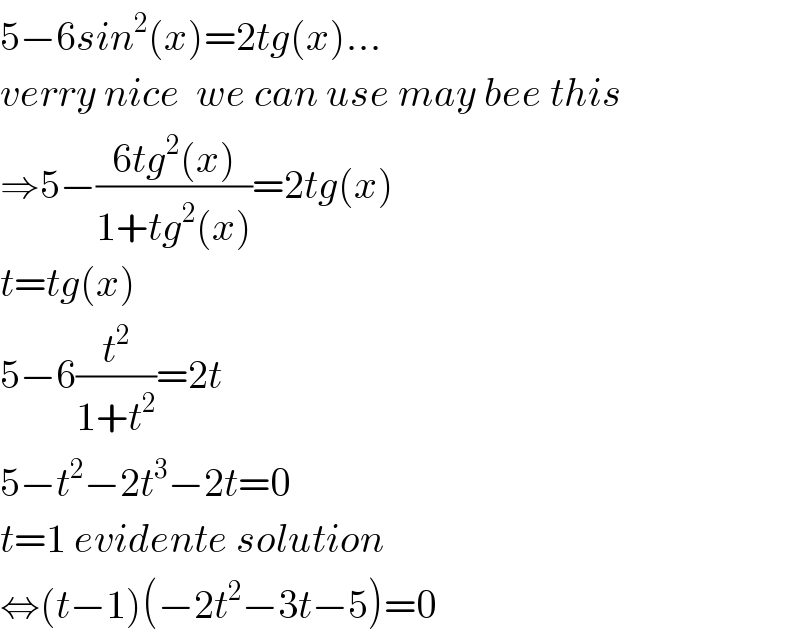
$$\mathrm{5}−\mathrm{6}{sin}^{\mathrm{2}} \left({x}\right)=\mathrm{2}{tg}\left({x}\right)... \\ $$$${verry}\:{nice}\:\:{we}\:{can}\:{use}\:{may}\:{bee}\:{this} \\ $$$$\Rightarrow\mathrm{5}−\frac{\mathrm{6}{tg}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)}=\mathrm{2}{tg}\left({x}\right) \\ $$$${t}={tg}\left({x}\right) \\ $$$$\mathrm{5}−\mathrm{6}\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }=\mathrm{2}{t} \\ $$$$\mathrm{5}−{t}^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}=\mathrm{0} \\ $$$${t}=\mathrm{1}\:{evidente}\:{solution}\: \\ $$$$\Leftrightarrow\left({t}−\mathrm{1}\right)\left(−\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{5}\right)=\mathrm{0} \\ $$
