Question Number 103648 by Lordose last updated on 16/Jul/20

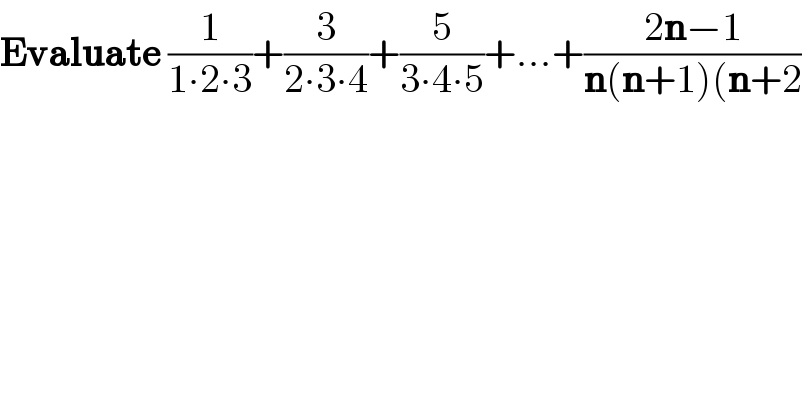
Evaluate (1/(1∙2∙3))+(3/(2∙3∙4))+(5/(3∙4∙5))+...+((2n−1)/(n(n+1)(n+2))

Answered by Dwaipayan Shikari last updated on 16/Jul/20

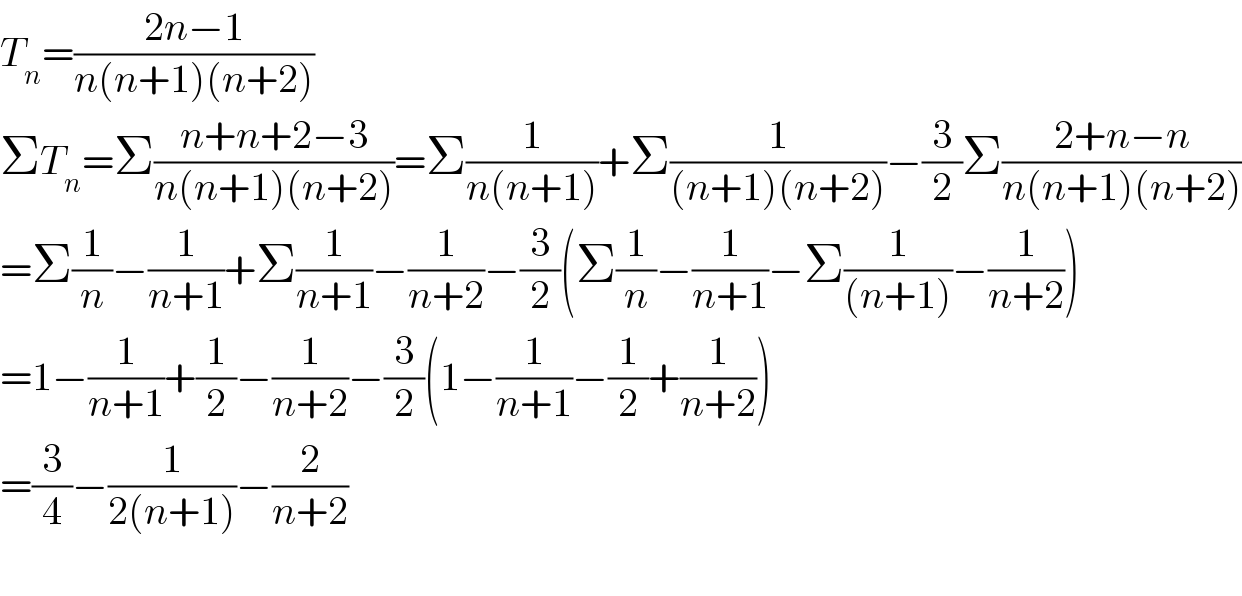
T_n =((2n−1)/(n(n+1)(n+2))) ΣT_n =Σ((n+n+2−3)/(n(n+1)(n+2)))=Σ(1/(n(n+1)))+Σ(1/((n+1)(n+2)))−(3/2)Σ((2+n−n)/(n(n+1)(n+2))) =Σ(1/n)−(1/(n+1))+Σ(1/(n+1))−(1/(n+2))−(3/2)(Σ(1/n)−(1/(n+1))−Σ(1/((n+1)))−(1/(n+2))) =1−(1/(n+1))+(1/2)−(1/(n+2))−(3/2)(1−(1/(n+1))−(1/2)+(1/(n+2))) =(3/4)−(1/(2(n+1)))−(2/(n+2))

Answered by mathmax by abdo last updated on 16/Jul/20

let A_n =Σ_(k=1) ^n ((2k−1)/(k(k+1)(k+2))) ⇒ let decompose F(x) =((2x−1)/(x(x+1)(x+2))) ⇒F(x) =(a/x)+(b/(x+1)) +(c/(x+2)) a =−(1/2) , b =((−3)/(−1)) =3 ,c =((−5)/((−2)(−1))) =−(5/2) ⇒F(x)=−(1/(2x))+(3/(x+1))−(5/(2(x+2))) ⇒A_n =Σ_(k=1) ^n F(k) =−(1/2)Σ_(k=1) ^n (1/k) +3Σ_(k=1) ^n (1/(k+1))−(5/2)Σ_(k=1) ^n (1/(k+2)) Σ_(k=1) ^n (1/k) =H_n Σ_(k=1) ^n (1/(k+1)) =Σ_(k=2) ^(n+1) (1/k) =Σ_(k=1) ^n (1/k) +(1/(n+1))−1 Σ_(k=1) ^n (1/(k+2)) =Σ_(k=3) ^(n+2) (1/k) =Σ_(k=1) ^n (1/k) +(1/(n+2))−(3/2) ⇒ A_n =−(1/2)H_n +3(H_n +(1/(n+1))−1)−(5/2)(H_n +(1/(n+2))−(3/2)) =−(1/2)H_n +3H_n −(5/2) H_n +(3/(n+1))−3 −(5/(2(n+2))) +((15)/4) =(3/(n+1))−(5/(2(n+2))) +((15)/4)−3 =(3/(n+1))−(5/(2(n+2))) +(3/4)