Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 103659 by abony1303 last updated on 16/Jul/20

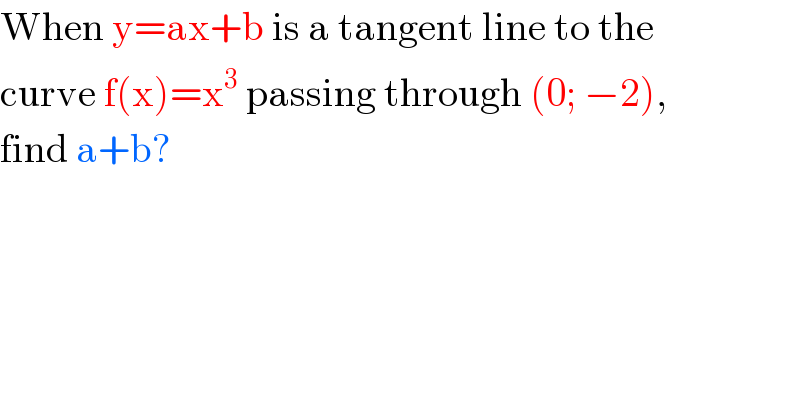
When y=ax+b is a tangent line to the curve f(x)=x^3 passing through (0; −2), find a+b?

$$\mathrm{When}\:\mathrm{y}=\mathrm{ax}+\mathrm{b}\:\mathrm{is}\:\mathrm{a}\:\mathrm{tangent}\:\mathrm{line}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{curve}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} \:\mathrm{passing}\:\mathrm{through}\:\left(\mathrm{0};\:−\mathrm{2}\right), \\ $$$$\mathrm{find}\:\mathrm{a}+\mathrm{b}? \\ $$

Commented by abony1303 last updated on 16/Jul/20

pls help

$$\mathrm{pls}\:\mathrm{help} \\ $$

Answered by Aziztisffola last updated on 16/Jul/20

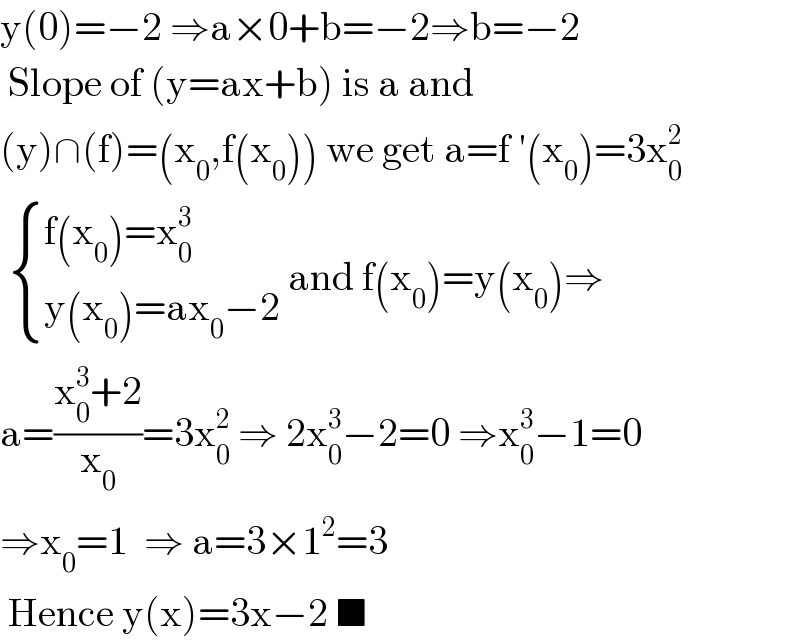
y(0)=−2 ⇒a×0+b=−2⇒b=−2 Slope of (y=ax+b) is a and (y)∩(f)=(x_0 ,f(x_0 )) we get a=f ′(x_0 )=3x_0 ^2 { ((f(x_0 )=x_0 ^3 )),((y(x_0 )=ax_0 −2)) :} and f(x_0 )=y(x_0 )⇒ a=((x_0 ^3 +2)/x_0 )=3x_0 ^2 ⇒ 2x_0 ^3 −2=0 ⇒x_0 ^3 −1=0 ⇒x_0 =1 ⇒ a=3×1^2 =3 Hence y(x)=3x−2 ■

$$\mathrm{y}\left(\mathrm{0}\right)=−\mathrm{2}\:\Rightarrow\mathrm{a}×\mathrm{0}+\mathrm{b}=−\mathrm{2}\Rightarrow\mathrm{b}=−\mathrm{2} \\ $$$$\:\mathrm{Slope}\:\mathrm{of}\:\left(\mathrm{y}=\mathrm{ax}+\mathrm{b}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{and} \\ $$$$\left(\mathrm{y}\right)\cap\left(\mathrm{f}\right)=\left(\mathrm{x}_{\mathrm{0}} ,\mathrm{f}\left(\mathrm{x}_{\mathrm{0}} \right)\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}=\mathrm{f}\:'\left(\mathrm{x}_{\mathrm{0}} \right)=\mathrm{3x}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\:\begin{cases}{\mathrm{f}\left(\mathrm{x}_{\mathrm{0}} \right)=\mathrm{x}_{\mathrm{0}} ^{\mathrm{3}} }\\{\mathrm{y}\left(\mathrm{x}_{\mathrm{0}} \right)=\mathrm{ax}_{\mathrm{0}} −\mathrm{2}}\end{cases}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{x}_{\mathrm{0}} \right)=\mathrm{y}\left(\mathrm{x}_{\mathrm{0}} \right)\Rightarrow \\ $$$$\mathrm{a}=\frac{\mathrm{x}_{\mathrm{0}} ^{\mathrm{3}} +\mathrm{2}}{\mathrm{x}_{\mathrm{0}} }=\mathrm{3x}_{\mathrm{0}} ^{\mathrm{2}} \:\Rightarrow\:\mathrm{2x}_{\mathrm{0}} ^{\mathrm{3}} −\mathrm{2}=\mathrm{0}\:\Rightarrow\mathrm{x}_{\mathrm{0}} ^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{0}} =\mathrm{1}\:\:\Rightarrow\:\mathrm{a}=\mathrm{3}×\mathrm{1}^{\mathrm{2}} =\mathrm{3} \\ $$$$\:\mathrm{Hence}\:\mathrm{y}\left(\mathrm{x}\right)=\mathrm{3x}−\mathrm{2}\:\blacksquare \\ $$

Answered by bemath last updated on 16/Jul/20

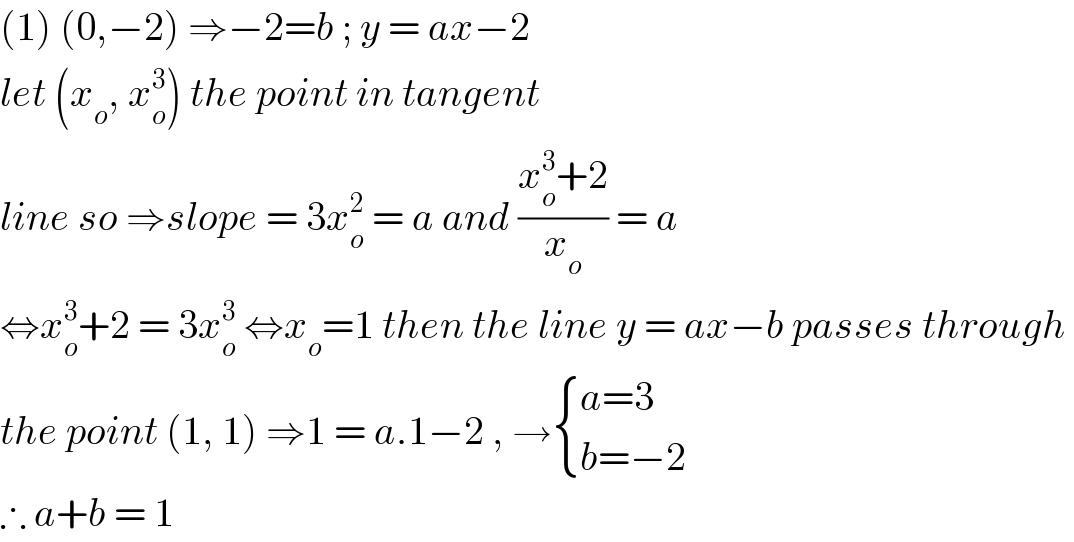
(1) (0,−2) ⇒−2=b ; y = ax−2 let (x_o , x_o ^3 ) the point in tangent line so ⇒slope = 3x_o ^2 = a and ((x_o ^3 +2)/x_o ) = a ⇔x_o ^3 +2 = 3x_o ^3 ⇔x_o =1 then the line y = ax−b passes through the point (1, 1) ⇒1 = a.1−2 , → { ((a=3)),((b=−2)) :} ∴ a+b = 1

$$\left(\mathrm{1}\right)\:\left(\mathrm{0},−\mathrm{2}\right)\:\Rightarrow−\mathrm{2}={b}\:;\:{y}\:=\:{ax}−\mathrm{2} \\ $$$${let}\:\left({x}_{{o}} ,\:{x}_{{o}} ^{\mathrm{3}} \right)\:{the}\:{point}\:{in}\:{tangent} \\ $$$${line}\:{so}\:\Rightarrow{slope}\:=\:\mathrm{3}{x}_{{o}} ^{\mathrm{2}} \:=\:{a}\:{and}\:\frac{{x}_{{o}} ^{\mathrm{3}} +\mathrm{2}}{{x}_{{o}} }\:=\:{a} \\ $$$$\Leftrightarrow{x}_{{o}} ^{\mathrm{3}} +\mathrm{2}\:=\:\mathrm{3}{x}_{{o}} ^{\mathrm{3}} \:\Leftrightarrow{x}_{{o}} =\mathrm{1}\:{then}\:{the}\:{line}\:{y}\:=\:{ax}−{b}\:{passes}\:{through}\: \\ $$$${the}\:{point}\:\left(\mathrm{1},\:\mathrm{1}\right)\:\Rightarrow\mathrm{1}\:=\:{a}.\mathrm{1}−\mathrm{2}\:,\:\rightarrow\begin{cases}{{a}=\mathrm{3}}\\{{b}=−\mathrm{2}}\end{cases} \\ $$$$\therefore\:{a}+{b}\:=\:\mathrm{1}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com