
Question Number 103669 by 175mohamed last updated on 16/Jul/20

$${prove}\:{that}\:: \\ $$$$\left.{a}\right)\:\int_{−\mathrm{3}} ^{−\mathrm{1}} {x}^{\mathrm{2}} {dx}\:\geqslant\int_{\mathrm{1}} ^{\mathrm{3}} \left(\mathrm{2}{x}−\mathrm{1}\right){dx} \\ $$$$\left.{b}\right)\int_{−\mathrm{2}} ^{\mathrm{0}} {xdx}\:\leqslant\int_{\mathrm{0}} ^{\mathrm{2}} \left({x}^{\mathrm{2}} \:+\:{x}\:\right){dx} \\ $$$$\left.{c}\right)\int_{\mathrm{1}} ^{\mathrm{4}} \left({x}^{\mathrm{2}} \:+\:\mathrm{2}\right){dx}\:\:\geqslant\int_{\mathrm{2}} ^{\mathrm{5}} \left(\mathrm{2}{x}\:−\mathrm{5}\right){dx} \\ $$$$\left.{d}\right)\int_{−\pi} ^{−\frac{\mathrm{3}\pi}{\mathrm{4}}} \mathrm{cos}\:\mathrm{2}{x}\:{dx}\:\geqslant\int_{\frac{\mathrm{3}\pi}{\mathrm{4}}} ^{\pi} \mathrm{sin}\:\mathrm{2}{x}\:{dx} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Aziztisffola last updated on 16/Jul/20

$$\mathrm{Just}\:\mathrm{calculat}\:\mathrm{each}\:\mathrm{integral}. \\ $$
Answered by abdomathmax last updated on 17/Jul/20
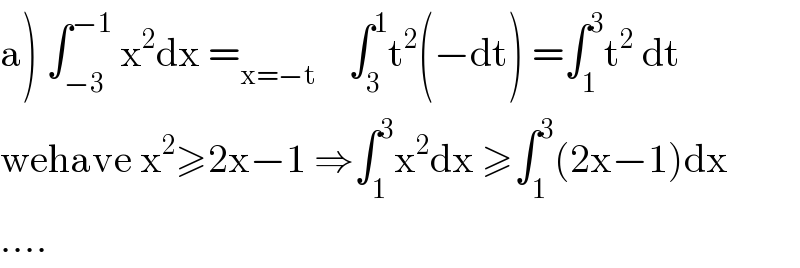
$$\left.\mathrm{a}\right)\:\int_{−\mathrm{3}} ^{−\mathrm{1}} \:\mathrm{x}^{\mathrm{2}} \mathrm{dx}\:=_{\mathrm{x}=−\mathrm{t}} \:\:\:\:\int_{\mathrm{3}} ^{\mathrm{1}} \mathrm{t}^{\mathrm{2}} \left(−\mathrm{dt}\right)\:=\int_{\mathrm{1}} ^{\mathrm{3}} \mathrm{t}^{\mathrm{2}} \:\mathrm{dt}\: \\ $$$$\mathrm{wehave}\:\mathrm{x}^{\mathrm{2}} \geqslant\mathrm{2x}−\mathrm{1}\:\Rightarrow\int_{\mathrm{1}} ^{\mathrm{3}} \mathrm{x}^{\mathrm{2}} \mathrm{dx}\:\geqslant\int_{\mathrm{1}} ^{\mathrm{3}} \left(\mathrm{2x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$.... \\ $$
