Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 103670 by bobhans last updated on 16/Jul/20

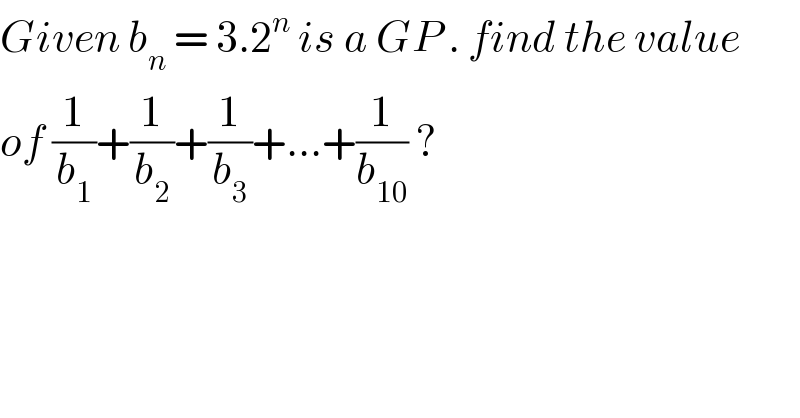
Given b_n = 3.2^n is a GP . find the value of (1/b_1 )+(1/b_2 )+(1/b_3 )+...+(1/b_(10) ) ?

$${Given}\:{b}_{{n}} \:=\:\mathrm{3}.\mathrm{2}^{{n}} \:{is}\:{a}\:{GP}\:.\:{find}\:{the}\:{value} \\ $$$${of}\:\frac{\mathrm{1}}{{b}_{\mathrm{1}} }+\frac{\mathrm{1}}{{b}_{\mathrm{2}} }+\frac{\mathrm{1}}{{b}_{\mathrm{3}} }+...+\frac{\mathrm{1}}{{b}_{\mathrm{10}} }\:?\: \\ $$

Answered by bramlex last updated on 16/Jul/20

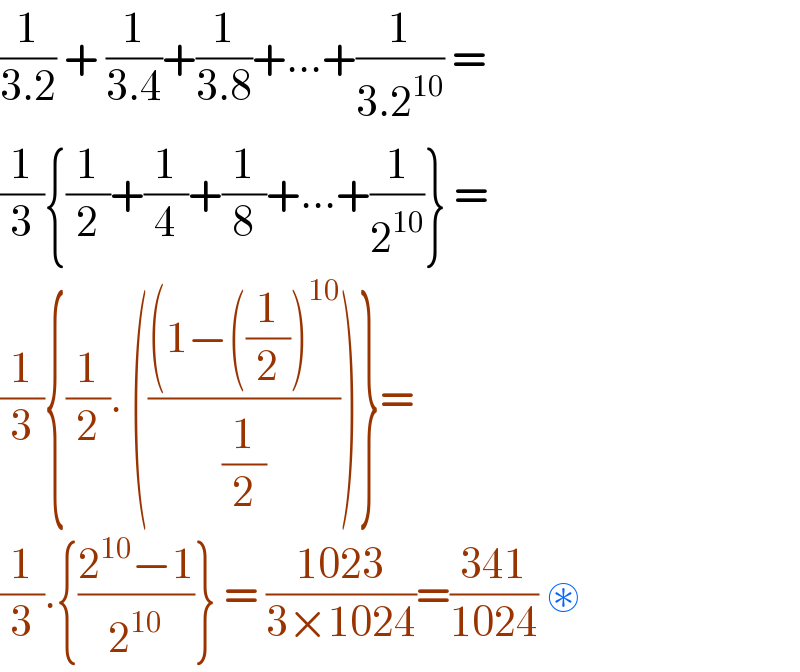
(1/(3.2)) + (1/(3.4))+(1/(3.8))+...+(1/(3.2^(10) )) = (1/3){(1/2)+(1/4)+(1/8)+...+(1/2^(10) )} = (1/3){(1/2). ((((1−((1/2))^(10) )/(1/2)))}= (1/3).{((2^(10) −1)/2^(10) )} = ((1023)/(3×1024))=((341)/(1024)) ⊛

$$\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{3}.\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}.\mathrm{8}}+...+\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}^{\mathrm{10}} }\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+...+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\right\}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{\mathrm{1}}{\mathrm{2}}.\:\left(\frac{\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{10}} \right.}{\frac{\mathrm{1}}{\mathrm{2}}}\right)\right\}= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}.\left\{\frac{\mathrm{2}^{\mathrm{10}} −\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\right\}\:=\:\frac{\mathrm{1023}}{\mathrm{3}×\mathrm{1024}}=\frac{\mathrm{341}}{\mathrm{1024}}\:\circledast \\ $$

Answered by Worm_Tail last updated on 16/Jul/20

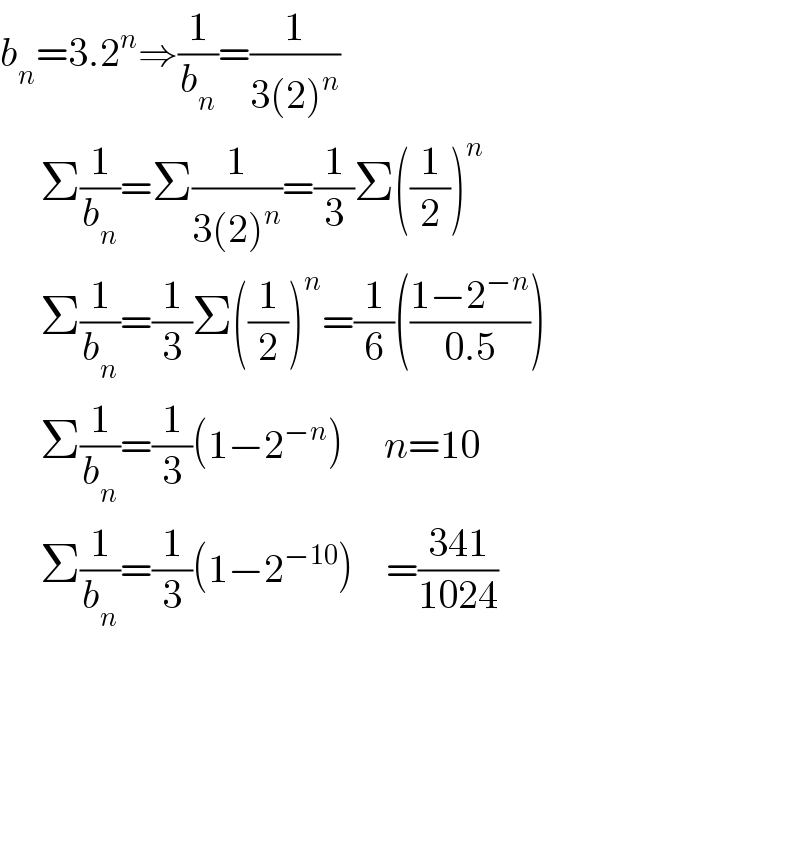
b_n =3.2^n ⇒(1/b_n )=(1/(3(2)^n )) Σ(1/b_n )=Σ(1/(3(2)^n ))=(1/3)Σ((1/2))^n Σ(1/b_n )=(1/3)Σ((1/2))^n =(1/6)(((1−2^(−n) )/(0.5))) Σ(1/b_n )=(1/3)(1−2^(−n) ) n=10 Σ(1/b_n )=(1/3)(1−2^(−10) ) =((341)/(1024))

$${b}_{{n}} =\mathrm{3}.\mathrm{2}^{{n}} \Rightarrow\frac{\mathrm{1}}{{b}_{{n}} }=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{2}\right)^{{n}} } \\ $$$$\:\:\:\:\:\Sigma\frac{\mathrm{1}}{{b}_{{n}} }=\Sigma\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{2}\right)^{{n}} }=\frac{\mathrm{1}}{\mathrm{3}}\Sigma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$$\:\:\:\:\:\Sigma\frac{\mathrm{1}}{{b}_{{n}} }=\frac{\mathrm{1}}{\mathrm{3}}\Sigma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} =\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{1}−\mathrm{2}^{−{n}} }{\mathrm{0}.\mathrm{5}}\right) \\ $$$$\:\:\:\:\:\Sigma\frac{\mathrm{1}}{{b}_{{n}} }=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}−\mathrm{2}^{−{n}} \right)\:\:\:\:\:{n}=\mathrm{10} \\ $$$$\:\:\:\:\:\Sigma\frac{\mathrm{1}}{{b}_{{n}} }=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}−\mathrm{2}^{−\mathrm{10}} \right)\:\:\:\:=\frac{\mathrm{341}}{\mathrm{1024}} \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\: \\ $$

Answered by Dwaipayan Shikari last updated on 16/Jul/20

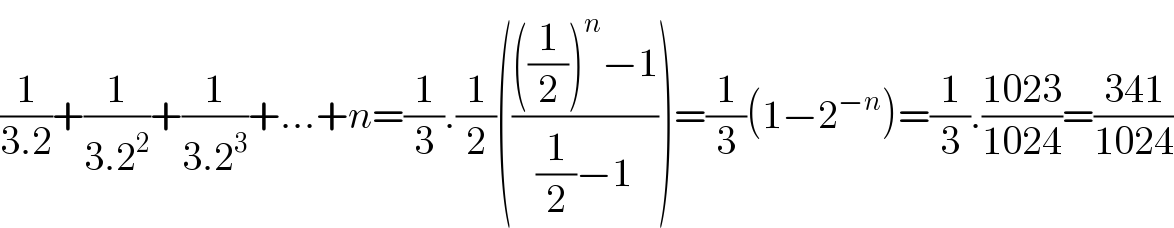
(1/(3.2))+(1/(3.2^2 ))+(1/(3.2^3 ))+...+n=(1/3).(1/2)(((((1/2))^n −1)/((1/2)−1)))=(1/3)(1−2^(−n) )=(1/3).((1023)/(1024))=((341)/(1024))

$$\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}^{\mathrm{3}} }+...+{n}=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} −\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}−\mathrm{2}^{−{n}} \right)=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{1023}}{\mathrm{1024}}=\frac{\mathrm{341}}{\mathrm{1024}} \\ $$

Answered by mathmax by abdo last updated on 16/Jul/20

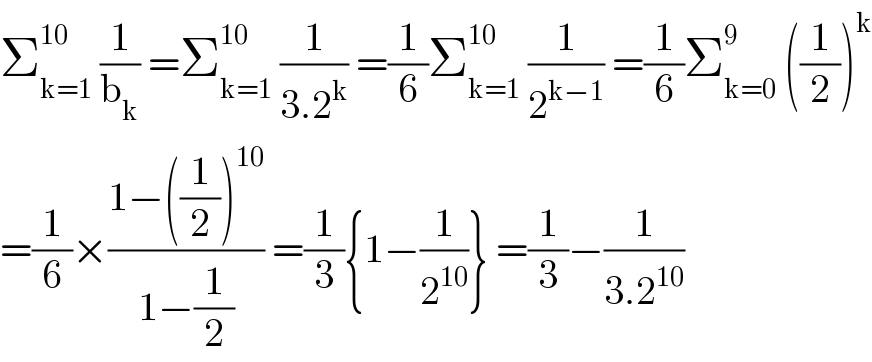
Σ_(k=1) ^(10) (1/b_k ) =Σ_(k=1) ^(10) (1/(3.2^k )) =(1/6)Σ_(k=1) ^(10) (1/2^(k−1) ) =(1/6)Σ_(k=0) ^9 ((1/2))^k =(1/6)×((1−((1/2))^(10) )/(1−(1/2))) =(1/3){1−(1/2^(10) )} =(1/3)−(1/(3.2^(10) ))

$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{10}} \:\frac{\mathrm{1}}{\mathrm{b}_{\mathrm{k}} }\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{10}} \:\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}^{\mathrm{k}} }\:=\frac{\mathrm{1}}{\mathrm{6}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{10}} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{1}} }\:=\frac{\mathrm{1}}{\mathrm{6}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{9}} \:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{10}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{3}}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\right\}\:=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}^{\mathrm{10}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com