Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 103673 by bobhans last updated on 16/Jul/20

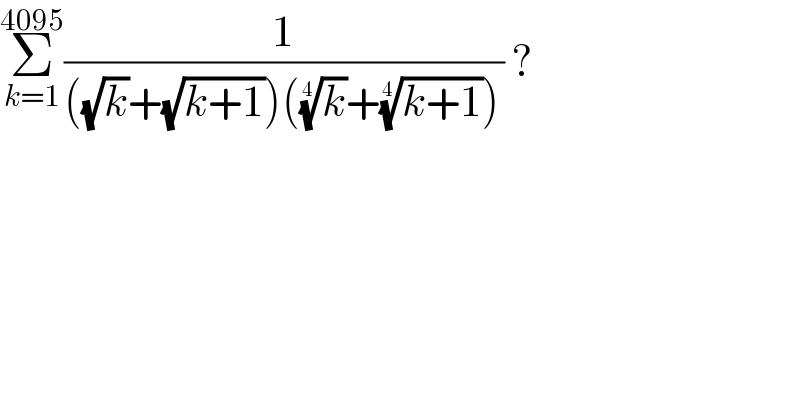
Σ_(k=1) ^(4095) (1/(((√k)+(√(k+1)))((k)^(1/4) +((k+1))^(1/4) ))) ?

$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{4095}} {\sum}}\frac{\mathrm{1}}{\left(\sqrt{{k}}+\sqrt{{k}+\mathrm{1}}\right)\left(\sqrt[{\mathrm{4}}]{{k}}+\sqrt[{\mathrm{4}}]{{k}+\mathrm{1}}\right)}\:? \\ $$

Answered by bramlex last updated on 16/Jul/20

(1/(((√k)+(√(k+1)))((k)^(1/4) +((k+1))^(1/4) ))) ×((((k+1))^(1/4) −(k)^(1/4) )/(((k+1))^(1/4) −(k)^(1/4) ))= ((((k+1))^(1/4) −(k)^(1/4) )/(((√(k+1))+(√k))((√(k+1))−(√k)))) = ((k+1))^(1/4) −(k)^(1/4) now S= Σ_(k=1) ^(4095) (((k+1))^(1/4) −(k)^(1/4) ) =((4096))^(1/4) −1=7 (note telecoping series)

$$\frac{\mathrm{1}}{\left(\sqrt{\mathrm{k}}+\sqrt{\mathrm{k}+\mathrm{1}}\right)\left(\sqrt[{\mathrm{4}}]{\mathrm{k}}+\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}\right)}\:×\frac{\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}}{\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}}= \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}}{\left(\sqrt{\mathrm{k}+\mathrm{1}}+\sqrt{\mathrm{k}}\right)\left(\sqrt{\mathrm{k}+\mathrm{1}}−\sqrt{\mathrm{k}}\right)}\:=\:\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}} \\ $$$$\mathrm{now}\:\mathrm{S}=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{4095}} {\sum}}\left(\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}\right)\:=\sqrt[{\mathrm{4}}]{\mathrm{4096}}−\mathrm{1}=\mathrm{7} \\ $$$$\left(\mathrm{note}\:\mathrm{telecoping}\:\mathrm{series}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com