Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 103716 by mr W last updated on 16/Jul/20

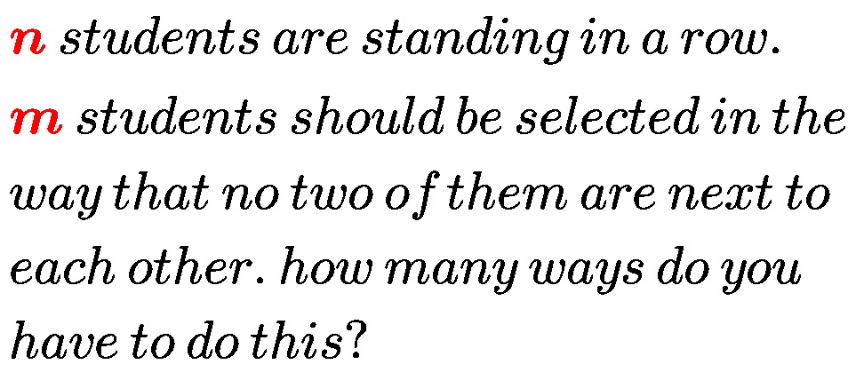
Commented by mr W last updated on 16/Jul/20

after thinking about it for two days, i think i have found the general solution which is simply C_m ^(n−m+1) . please give a try, prove or disprove it!

$${after}\:{thinking}\:{about}\:{it}\:{for}\:{two}\:{days}, \\ $$$${i}\:{think}\:{i}\:{have}\:{found}\:{the}\:{general} \\ $$$${solution}\:{which}\:{is}\:{simply} \\ $$$$\boldsymbol{{C}}_{\boldsymbol{{m}}} ^{\boldsymbol{{n}}−\boldsymbol{{m}}+\mathrm{1}} . \\ $$$${please}\:{give}\:{a}\:{try},\:{prove}\:{or}\:{disprove}\:{it}! \\ $$

Commented by prakash jain last updated on 16/Jul/20

s_1 s_2 s_3 s_4 ...s_n if we draw m bars and select student to the left of bar we have total n postion for bars. s_1 ∙ s_2 ∙ s_3 ∙s_4 ∙...∙s_n So for example 6,2 case s∣ s s s s∣ s We need m bars, the first bar can have 1 or more students to the left. The remaining bars can only have 2 or more student to the left of bar. 0 or more student can be present after last bar. Σ_(i=1) ^n x(Σ_(i=2) ^n x^2 )^(m−1) Σ_(i=0) ^n x^i ((x(1−x^n ))/(1−x))×((x^(2(m−1)) (1−x^(n−1) )^(m−1) )/((1−x)^(m−1) ))×(((1−x^(n+1) ))/(1−x)) m≥1 =x^(2m−1) ×(1/((1−x)^(m+1) )) =x^(2m−1) Σ_(i=0) ^∞ C_i ^(m+i) x^i sum of student must be n 2m−1+i=n⇒i=n+1−2m Required result C_(n+1−2m) ^(m+n+1−2m) =C_(n+1−2m) ^(n−m+1) =C_((n−m+1)−(n+1−2m)) ^(n−m+1) =C_m ^(n−m+1) Please feedback.

$$\mathrm{s}_{\mathrm{1}} \:\mathrm{s}_{\mathrm{2}} \:\:\mathrm{s}_{\mathrm{3}} \:\:\mathrm{s}_{\mathrm{4}} \:...\mathrm{s}_{\mathrm{n}} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{draw}\:{m}\:\mathrm{bars}\:\mathrm{and}\:\mathrm{select} \\ $$$$\mathrm{student}\:\mathrm{to}\:\mathrm{the}\:\mathrm{left}\:\mathrm{of}\:\mathrm{bar}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{total}\:\mathrm{n}\:\mathrm{postion}\:\mathrm{for}\:\mathrm{bars}. \\ $$$$\mathrm{s}_{\mathrm{1}} \centerdot\:\mathrm{s}_{\mathrm{2}} \centerdot\:\:\mathrm{s}_{\mathrm{3}} \:\:\centerdot\mathrm{s}_{\mathrm{4}} \:\centerdot...\centerdot\mathrm{s}_{\mathrm{n}} \\ $$$$\mathrm{So}\:\mathrm{for}\:\mathrm{example}\:\mathrm{6},\mathrm{2}\:\mathrm{case} \\ $$$$\mathrm{s}\mid\:\mathrm{s}\:\mathrm{s}\:\mathrm{s}\:\mathrm{s}\mid\:\mathrm{s} \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{m}\:\mathrm{bars}, \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{bar}\:\mathrm{can}\:\mathrm{have}\:\mathrm{1}\:\mathrm{or}\:\mathrm{more} \\ $$$$\mathrm{students}\:\mathrm{to}\:\mathrm{the}\:\mathrm{left}.\:\mathrm{The}\:\mathrm{remaining} \\ $$$$\mathrm{bars}\:\mathrm{can}\:\mathrm{only}\:\mathrm{have}\:\mathrm{2}\:\mathrm{or}\:\mathrm{more} \\ $$$$\mathrm{student}\:\mathrm{to}\:\mathrm{the}\:\mathrm{left}\:\mathrm{of}\:\mathrm{bar}. \\ $$$$\mathrm{0}\:\mathrm{or}\:\mathrm{more}\:\mathrm{student}\:\mathrm{can}\:\mathrm{be}\:\mathrm{present} \\ $$$$\mathrm{after}\:\mathrm{last}\:\mathrm{bar}. \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}\left(\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}{x}^{\mathrm{2}} \right)^{{m}−\mathrm{1}} \underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} \\ $$$$\frac{{x}\left(\mathrm{1}−{x}^{{n}} \right)}{\mathrm{1}−{x}}×\frac{{x}^{\mathrm{2}\left({m}−\mathrm{1}\right)} \left(\mathrm{1}−{x}^{{n}−\mathrm{1}} \right)^{{m}−\mathrm{1}} }{\left(\mathrm{1}−{x}\right)^{{m}−\mathrm{1}} }×\frac{\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)}{\mathrm{1}−{x}} \\ $$$${m}\geqslant\mathrm{1} \\ $$$$={x}^{\mathrm{2}{m}−\mathrm{1}} ×\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{{m}+\mathrm{1}} } \\ $$$$={x}^{\mathrm{2}{m}−\mathrm{1}} \underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{i}} ^{{m}+{i}} {x}^{{i}} \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{student}\:\mathrm{must}\:\mathrm{be}\:{n} \\ $$$$\mathrm{2}{m}−\mathrm{1}+{i}={n}\Rightarrow{i}={n}+\mathrm{1}−\mathrm{2}{m} \\ $$$$\mathrm{Required}\:\mathrm{result} \\ $$$$\mathrm{C}_{{n}+\mathrm{1}−\mathrm{2}{m}} ^{{m}+{n}+\mathrm{1}−\mathrm{2}{m}} ={C}_{{n}+\mathrm{1}−\mathrm{2}{m}} ^{{n}−{m}+\mathrm{1}} \\ $$$$={C}_{\left({n}−{m}+\mathrm{1}\right)−\left({n}+\mathrm{1}−\mathrm{2}{m}\right)} ^{{n}−{m}+\mathrm{1}} ={C}_{{m}} ^{{n}−{m}+\mathrm{1}} \\ $$$$\mathrm{Please}\:\mathrm{feedback}. \\ $$

Commented by mr W last updated on 16/Jul/20

correct sir!

$${correct}\:{sir}! \\ $$

Answered by mr W last updated on 17/Jul/20

this is my solution ★ stand for m selected students ♦⧫ stand for places for other students ♦★⧫★⧫★⧫★⧫...⧫★⧫★◊ ◊ may be empty or occupied by any number of students ⧫ must be occupied by at least one student we have two ◊ places, generating function of each one is 1+x+x^2 +x^3 +...=(1/(1−x)) we have (m−1) ⧫ places, generating function of each one is x+x^2 +x^3 +...=(x/(1−x)) the total number of students who occupy the ◊ and ⧫ places is (n−m). the number of ways to occupy these places is the coefficient of the x^(n−m) term of the following generating function (1+x+x^2 +x^3 +...)^2 (x+x^2 +x^3 +...)^(m−1) =((1/(1−x)))^2 ((x/(1−x)))^(m−1) =(x^(m−1) /((1−x)^(m+1) )) =x^(m−1) Σ_(k=0) ^∞ C_m ^(k+m) x^k m−1+k=n−m ⇒k+m=n−m+1 ⇒the coefficient of x^(n−m) term is therefore C_m ^(n−m+1) which is the answer we need.

$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{my}}\:\boldsymbol{{solution}} \\ $$$$ \\ $$$$\bigstar\:{stand}\:{for}\:{m}\:{selected}\:{students} \\ $$$$\diamondsuit\blacklozenge\:{stand}\:{for}\:{places}\:{for}\:{other}\:{students} \\ $$$$ \\ $$$$\diamondsuit\bigstar\blacklozenge\bigstar\blacklozenge\bigstar\blacklozenge\bigstar\blacklozenge...\blacklozenge\bigstar\blacklozenge\bigstar\lozenge \\ $$$$ \\ $$$$\lozenge\:{may}\:{be}\:{empty}\:{or}\:{occupied}\:{by}\:{any} \\ $$$${number}\:{of}\:{students} \\ $$$$\blacklozenge\:{must}\:{be}\:{occupied}\:{by}\:{at}\:{least}\:{one} \\ $$$${student} \\ $$$$ \\ $$$${we}\:{have}\:{two}\:\lozenge\:{places},\:{generating} \\ $$$${function}\:{of}\:{each}\:{one}\:{is} \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$ \\ $$$${we}\:{have}\:\left({m}−\mathrm{1}\right)\:\blacklozenge\:{places},\:{generating} \\ $$$${function}\:{of}\:{each}\:{one}\:{is} \\ $$$${x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...=\frac{{x}}{\mathrm{1}−{x}} \\ $$$$ \\ $$$${the}\:{total}\:{number}\:{of}\:{students}\:{who} \\ $$$${occupy}\:{the}\:\lozenge\:{and}\:\blacklozenge\:{places}\:{is}\:\left({n}−{m}\right). \\ $$$$ \\ $$$${the}\:{number}\:{of}\:{ways}\:{to}\:{occupy}\:{these} \\ $$$${places}\:{is}\:{the}\:{coefficient}\:{of}\:{the}\:{x}^{{n}−{m}} \\ $$$${term}\:{of}\:{the}\:{following}\:{generating} \\ $$$${function} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...\right)^{\mathrm{2}} \left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...\right)^{{m}−\mathrm{1}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)^{\mathrm{2}} \left(\frac{{x}}{\mathrm{1}−{x}}\right)^{{m}−\mathrm{1}} =\frac{{x}^{{m}−\mathrm{1}} }{\left(\mathrm{1}−{x}\right)^{{m}+\mathrm{1}} } \\ $$$$={x}^{{m}−\mathrm{1}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{m}} ^{{k}+{m}} {x}^{{k}} \\ $$$${m}−\mathrm{1}+{k}={n}−{m}\:\Rightarrow{k}+{m}={n}−{m}+\mathrm{1} \\ $$$$\Rightarrow{the}\:{coefficient}\:{of}\:{x}^{{n}−{m}} \:{term}\:{is} \\ $$$${therefore}\:{C}_{{m}} ^{{n}−{m}+\mathrm{1}} \:{which}\:{is}\:{the} \\ $$$${answer}\:{we}\:{need}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com