Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 103741 by mathmax by abdo last updated on 17/Jul/20

$$\mathrm{calculate}{\int }_0^{\mathrm{\infty }}\frac{\arctan \left(\mathrm{ch}\left(\mathrm{x}\right)\right)}{{\mathrm{x}}^2+9}\mathrm{dx}$$

Answered by mathmax by abdo last updated on 17/Jul/20

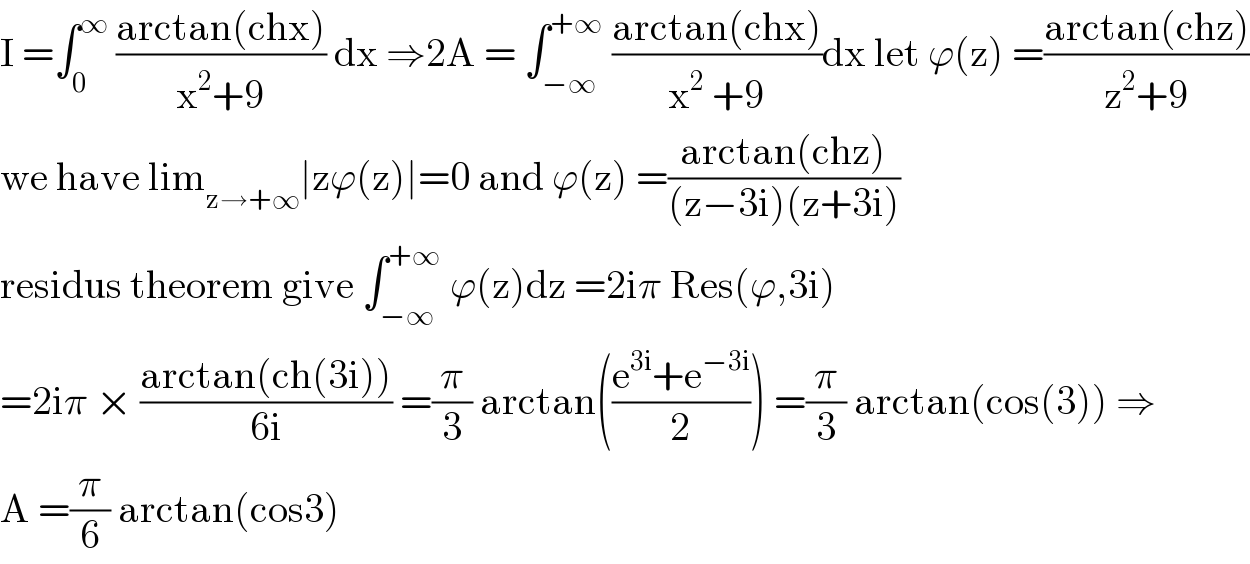
$$\mathrm{I}={\int }_0^{\mathrm{\infty }}\frac{\arctan \left(\mathrm{chx}\right)}{{\mathrm{x}}^2+9}\mathrm{dx}\Rightarrow 2\mathrm{A}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\arctan \left(\mathrm{chx}\right)}{{\mathrm{x}}^2+9}\mathrm{dx}\mathrm{let}\phi \left(\mathrm{z}\right)=\frac{\arctan \left(\mathrm{chz}\right)}{{\mathrm{z}}^2+9}$$$$\mathrm{we}\mathrm{have}{\lim }_{\mathrm{z}\to +\mathrm{\infty }}\mid \mathrm{z}\phi \left(\mathrm{z}\right)\mid =0\mathrm{and}\phi \left(\mathrm{z}\right)=\frac{\arctan \left(\mathrm{chz}\right)}{(\mathrm{z}-3\mathrm{i})(\mathrm{z}+3\mathrm{i})}$$$$\mathrm{residus}\mathrm{theorem}\mathrm{give}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\phi \left(\mathrm{z}\right)\mathrm{dz}=2\mathrm{i}\pi \mathrm{Res}(\phi ,3\mathrm{i})$$$$=2\mathrm{i}\pi \times \frac{\arctan \left(\mathrm{ch}\left(3\mathrm{i}\right)\right)}{6\mathrm{i}}=\frac{\pi }{3}\arctan \left(\frac{{\mathrm{e}}^{3\mathrm{i}}+{\mathrm{e}}^{-3\mathrm{i}}}{2}\right)=\frac{\pi }{3}\arctan \left(\cos \left(3\right)\right)\Rightarrow$$$$\mathrm{A}=\frac{\pi }{6}\arctan \left(\cos 3\right)$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com