
Question Number 103751 by hardylanes last updated on 17/Jul/20
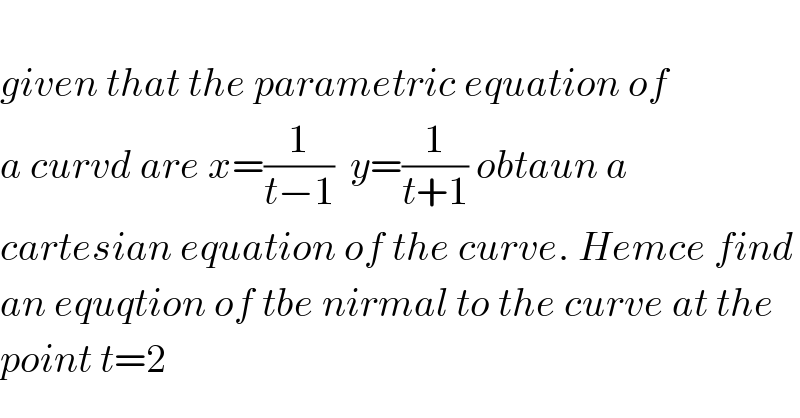
$$ \\ $$$${given}\:{that}\:{the}\:{parametric}\:{equation}\:{of}\: \\ $$$${a}\:{curvd}\:{are}\:{x}=\frac{\mathrm{1}}{{t}−\mathrm{1}}\:\:{y}=\frac{\mathrm{1}}{{t}+\mathrm{1}}\:{obtaun}\:{a}\: \\ $$$${cartesian}\:{equation}\:{of}\:{the}\:{curve}.\:{Hemce}\:{find} \\ $$$${an}\:{equqtion}\:{of}\:{tbe}\:{nirmal}\:{to}\:{the}\:{curve}\:{at}\:{the}\: \\ $$$${point}\:{t}=\mathrm{2} \\ $$
Answered by bobhans last updated on 17/Jul/20
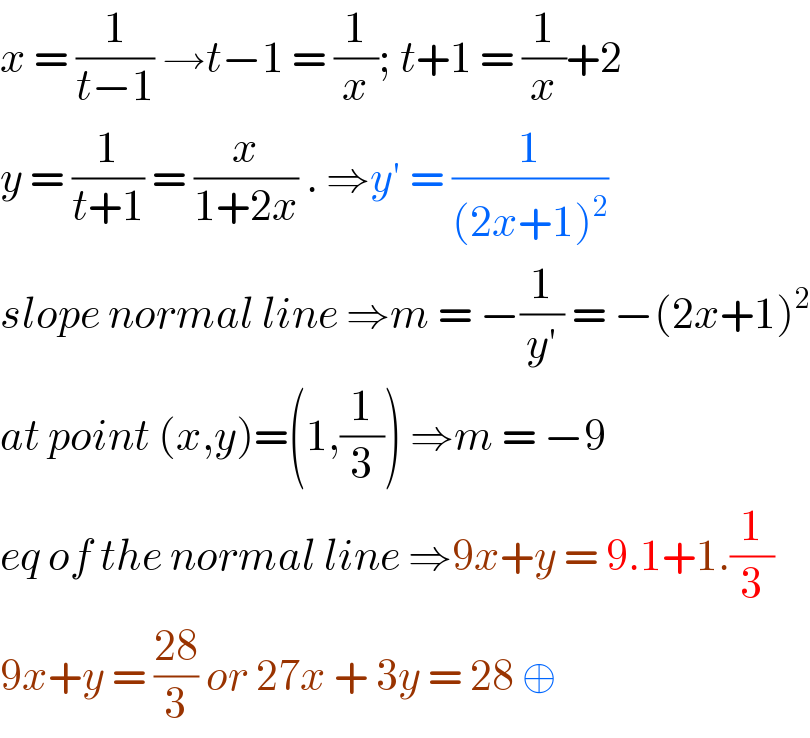
$${x}\:=\:\frac{\mathrm{1}}{{t}−\mathrm{1}}\:\rightarrow{t}−\mathrm{1}\:=\:\frac{\mathrm{1}}{{x}};\:{t}+\mathrm{1}\:=\:\frac{\mathrm{1}}{{x}}+\mathrm{2} \\ $$$${y}\:=\:\frac{\mathrm{1}}{{t}+\mathrm{1}}\:=\:\frac{{x}}{\mathrm{1}+\mathrm{2}{x}}\:.\:\Rightarrow{y}'\:=\:\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${slope}\:{normal}\:{line}\:\Rightarrow{m}\:=\:−\frac{\mathrm{1}}{{y}'}\:=\:−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${at}\:{point}\:\left({x},{y}\right)=\left(\mathrm{1},\frac{\mathrm{1}}{\mathrm{3}}\right)\:\Rightarrow{m}\:=\:−\mathrm{9} \\ $$$${eq}\:{of}\:{the}\:{normal}\:{line}\:\Rightarrow\mathrm{9}{x}+{y}\:=\:\mathrm{9}.\mathrm{1}+\mathrm{1}.\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{9}{x}+{y}\:=\:\frac{\mathrm{28}}{\mathrm{3}}\:{or}\:\mathrm{27}{x}\:+\:\mathrm{3}{y}\:=\:\mathrm{28}\:\oplus\: \\ $$
Commented by bobhans last updated on 17/Jul/20
$${what}\:{do}\:{you}\:{meant}\:??? \\ $$
