
Previous in Differential Equation Next in Differential Equation
Question Number 103759 by bemath last updated on 17/Jul/20
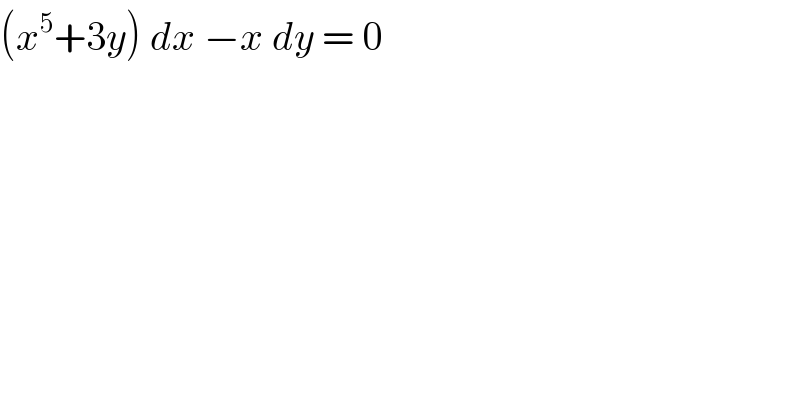
$$\left({x}^{\mathrm{5}} +\mathrm{3}{y}\right)\:{dx}\:−{x}\:{dy}\:=\:\mathrm{0}\: \\ $$
Answered by MAB last updated on 17/Jul/20
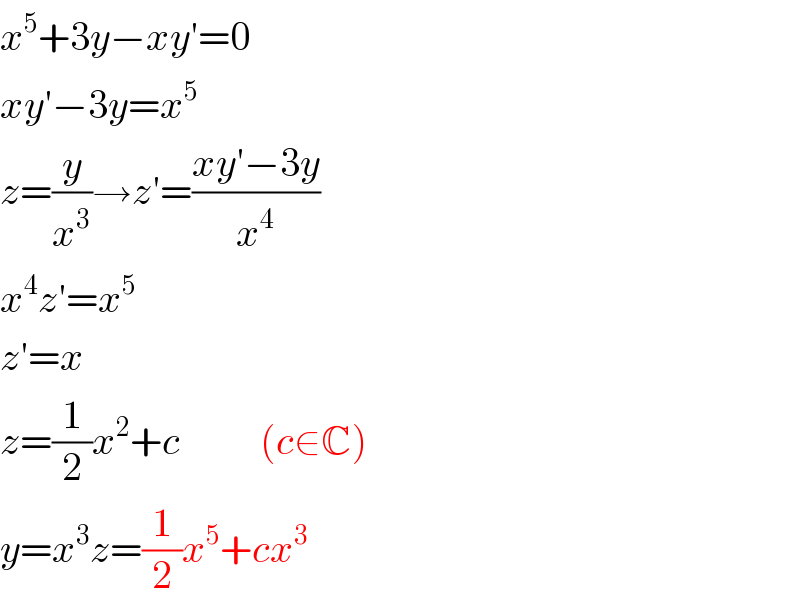
$${x}^{\mathrm{5}} +\mathrm{3}{y}−{xy}'=\mathrm{0} \\ $$$${xy}'−\mathrm{3}{y}={x}^{\mathrm{5}} \\ $$$${z}=\frac{{y}}{{x}^{\mathrm{3}} }\rightarrow{z}'=\frac{{xy}'−\mathrm{3}{y}}{{x}^{\mathrm{4}} } \\ $$$${x}^{\mathrm{4}} {z}'={x}^{\mathrm{5}} \\ $$$${z}'={x} \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{c}\:\:\:\:\:\:\:\:\:\:\left({c}\in\mathbb{C}\right) \\ $$$${y}={x}^{\mathrm{3}} {z}=\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{5}} +{cx}^{\mathrm{3}} \\ $$
Answered by john santu last updated on 17/Jul/20

$${x}\:\frac{{dy}}{{dx}}\:−\mathrm{3}{y}\:=\:{x}^{\mathrm{5}} \: \\ $$$$\frac{{dy}}{{dx}}−\:\frac{\mathrm{3}}{{x}}{y}\:=\:{x}^{\mathrm{4}} \: \\ $$$${Integrating}\:{factor}\: \\ $$$${IF}\:{u}\left({x}\right)\:=\:{e}^{\int−\frac{\mathrm{3}}{{x}}\:{dx}} =\:{e}^{\mathrm{ln}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)} \\ $$$${u}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:\Rightarrow{y}\:=\:\frac{\int\frac{\mathrm{1}}{{x}^{\mathrm{3}} }.{x}^{\mathrm{4}} \:{dx}+{C}}{\frac{\mathrm{1}}{{x}^{\mathrm{3}} }} \\ $$$${y}\:=\:{x}^{\mathrm{3}} \left\{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{C}\right\}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{5}} +{Cx}^{\mathrm{3}} \\ $$$$\left({JS}\:\circledast\right)\: \\ $$
Commented by Ar Brandon last updated on 17/Jul/20
��
Answered by bemath last updated on 17/Jul/20

