
Previous in Differential Equation Next in Differential Equation
Question Number 103769 by bemath last updated on 17/Jul/20
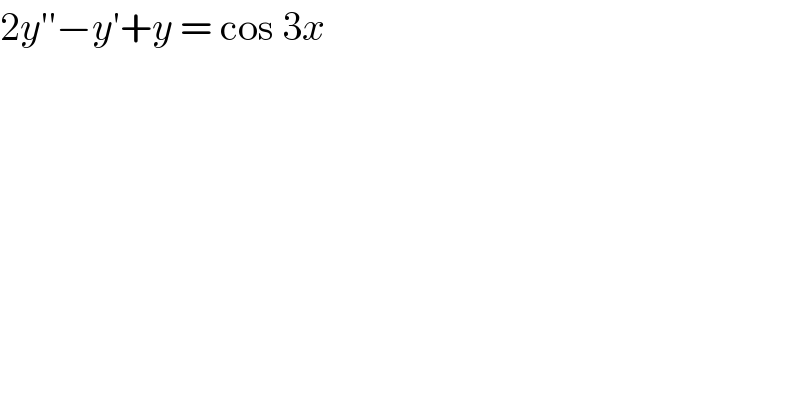
$$\mathrm{2}{y}''−{y}'+{y}\:=\:\mathrm{cos}\:\mathrm{3}{x} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/20
![let solve by laplace transform e ⇒2L(y^(′′) )−L(y^′ )+L(y) =L(cos(3x)) ⇒ 2{x^2 L(y)−xy(o)−y^′ (o)}−(xL(y)−y(o)) +L(y) =L(cos(3x)) ⇒ (2x^2 −x+1)L(y)−(2x−1)y(o)−2y^′ (o) =L(cos(3x)) ⇒ (2x^2 −x+1)L(y) =(2x−1)y(0)+2y^′ (o)+L(cos(3x)) L(cos(3x))=∫_0 ^∞ cos(3t)e^(−xt) dt =Re(∫_0 ^∞ e^((−x+3i)t) dt) and ∫_0 ^∞ e^((−x+3i)t) dt =[(1/(−x+3i))e^((−x+3i)t) ]_0 ^∞ =−(1/(−x+3i)) =(1/(x−3i)) =((x+3i)/(x^2 +9)) ⇒ L(cos(3x)) =(x/(x^2 +9)) e ⇒L(y) =((2x−1)/((2x^2 −x+1)))y(o)+(2/(2x^2 −x+1))y^′ (o) +(x/((x^2 +9)(2x^2 −x+1))) ⇒ y(x) =y(o)L^(−1) (((2x−1)/(2x^2 −x+1)))+2y^′ (0)L^(−1) ((1/(2x^2 −x+1)))+L^(−1) ((x/((x^2 +9)(2x^2 −x+1)))) f(x) =((2x−1)/(2x^2 −x+1)) Δ =1−8 =−7 ⇒x_1 =((1+i(√7))/4) and x_2 =((1−i(√7))/2) f(x) =((2x−1)/(2(x−x_1 )(x−x_2 ))) =(a/(x−x_1 )) +(b/(x−x_2 )) eazy to find a and b ⇒ L^(−1) (f) =a e^(x_1 x) +b e^(x_2 x) →e^(x/2) { a^′ cos(((√7)/2)x) +b^′ sin(((√7)/2)x)} L^(−1) ((1/(2x^2 −x+1))) =e^(x/2) (α cos(((√7)/2)x) +βsin(((√7)/2)x)} g(x) =(x/((x^2 +9)(2x^2 −x+1))) =(a/(x−3i)) +(b/(x+3i)) +(c/(x−x_1 )) +(d/(x−x_2 )) ⇒ L^(−1) (g) =a e^(3ix) +b e^(−3ix) + e^(x/2) { α cos(((√7)/2)x) +βsis(((√7)/2)x)} =a^′ cos(3x) +b^′ sin(3x) +e^(x/2) {α cos(((√7)/2)x) +β sin(((√7)/2)x)}...](Q103814.png)
$$\mathrm{let}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{laplace}\:\mathrm{transform} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{2L}\left(\mathrm{y}^{''} \right)−\mathrm{L}\left(\mathrm{y}^{'} \right)+\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{cos}\left(\mathrm{3x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{2}\left\{\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{o}\right)−\mathrm{y}^{'} \left(\mathrm{o}\right)\right\}−\left(\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{o}\right)\right)\:+\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{cos}\left(\mathrm{3x}\right)\right)\:\Rightarrow \\ $$$$\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)−\left(\mathrm{2x}−\mathrm{1}\right)\mathrm{y}\left(\mathrm{o}\right)−\mathrm{2y}^{'} \left(\mathrm{o}\right)\:=\mathrm{L}\left(\mathrm{cos}\left(\mathrm{3x}\right)\right)\:\Rightarrow \\ $$$$\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\left(\mathrm{2x}−\mathrm{1}\right)\mathrm{y}\left(\mathrm{0}\right)+\mathrm{2y}^{'} \left(\mathrm{o}\right)+\mathrm{L}\left(\mathrm{cos}\left(\mathrm{3x}\right)\right) \\ $$$$\mathrm{L}\left(\mathrm{cos}\left(\mathrm{3x}\right)\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{3t}\right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dt}\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \mathrm{dt}\right)\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{3i}}\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:=−\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{3i}}\:=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{3i}}\:=\frac{\mathrm{x}+\mathrm{3i}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{cos}\left(\mathrm{3x}\right)\right)\:=\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{2x}−\mathrm{1}}{\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\mathrm{y}\left(\mathrm{o}\right)+\frac{\mathrm{2}}{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{y}^{'} \left(\mathrm{o}\right)\:+\frac{\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9}\right)\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{y}\left(\mathrm{o}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right)+\mathrm{2y}^{'} \left(\mathrm{0}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right)+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}} \\ $$$$\Delta\:=\mathrm{1}−\mathrm{8}\:=−\mathrm{7}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{7}}}{\mathrm{4}}\:\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{2}\left(\mathrm{x}−\mathrm{x}_{\mathrm{1}} \right)\left(\mathrm{x}−\mathrm{x}_{\mathrm{2}} \right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{x}_{\mathrm{1}} }\:+\frac{\mathrm{b}}{\mathrm{x}−\mathrm{x}_{\mathrm{2}} }\:\:\mathrm{eazy}\:\mathrm{to}\:\mathrm{find}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\right)\:=\mathrm{a}\:\mathrm{e}^{\mathrm{x}_{\mathrm{1}} \mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{\mathrm{x}_{\mathrm{2}} \mathrm{x}} \:\rightarrow\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \left\{\:\mathrm{a}^{'} \:\mathrm{cos}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\:+\mathrm{b}^{'} \mathrm{sin}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\right\} \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right)\:=\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \left(\alpha\:\mathrm{cos}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\:+\beta\mathrm{sin}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\right\} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{3i}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{3i}}\:+\frac{\mathrm{c}}{\mathrm{x}−\mathrm{x}_{\mathrm{1}} }\:+\frac{\mathrm{d}}{\mathrm{x}−\mathrm{x}_{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{g}\right)\:=\mathrm{a}\:\mathrm{e}^{\mathrm{3ix}} \:+\mathrm{b}\:\mathrm{e}^{−\mathrm{3ix}} \:+\:\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \left\{\:\alpha\:\mathrm{cos}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\:+\beta\mathrm{sis}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\right\} \\ $$$$=\mathrm{a}^{'} \:\mathrm{cos}\left(\mathrm{3x}\right)\:+\mathrm{b}^{'} \:\mathrm{sin}\left(\mathrm{3x}\right)\:+\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \left\{\alpha\:\mathrm{cos}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\:+\beta\:\mathrm{sin}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{x}\right)\right\}... \\ $$
