
Question Number 103773 by bemath last updated on 17/Jul/20
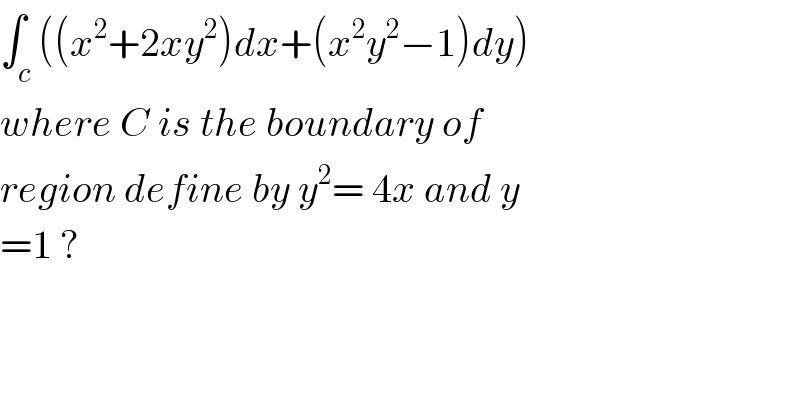
$$\int_{{c}} \left(\left({x}^{\mathrm{2}} +\mathrm{2}{xy}^{\mathrm{2}} \right){dx}+\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}\right){dy}\right) \\ $$$${where}\:{C}\:{is}\:{the}\:{boundary}\:{of} \\ $$$${region}\:{define}\:{by}\:{y}^{\mathrm{2}} =\:\mathrm{4}{x}\:{and}\:{y} \\ $$$$=\mathrm{1}\:? \\ $$
Answered by bramlex last updated on 17/Jul/20
![note that C is a closed curve . observe that y^2 =4x intersects x=1 when y = ± 2 Green′s Theorem yields ∫_c ((x^2 +2xy^2 )dx+(x^2 y^2 −1)dy)= ∫_(−2) ^2 ∫_(y^2 /4) ^1 (2xy^2 −4xy) dxdy =∫_(−2) ^2 {(x^2 y^2 −2x^2 y)}∣_(y^2 /4) ^1 dy = 2∫_0 ^2 (y^2 −(y^6 /(16))) dy [ even function] = [(2/3)y^3 −(y^7 /(112)) ]_9 ^2 = ((16)/3) −((128)/(112)) =((16)/3)−(8/7) = ((88)/(21))](Q103775.png)
$${note}\:{that}\:{C}\:{is}\:{a}\:{closed}\:{curve}\:. \\ $$$${observe}\:{that}\:{y}^{\mathrm{2}} =\mathrm{4}{x}\:{intersects} \\ $$$${x}=\mathrm{1}\:{when}\:{y}\:=\:\pm\:\mathrm{2} \\ $$$${Green}'{s}\:{Theorem}\:{yields} \\ $$$$\int_{{c}} \left(\left({x}^{\mathrm{2}} +\mathrm{2}{xy}^{\mathrm{2}} \right){dx}+\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{1}\right){dy}\right)= \\ $$$$\underset{−\mathrm{2}} {\overset{\mathrm{2}} {\int}}\:\underset{{y}^{\mathrm{2}} /\mathrm{4}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{2}{xy}^{\mathrm{2}} −\mathrm{4}{xy}\right)\:{dxdy}\: \\ $$$$=\underset{−\mathrm{2}} {\overset{\mathrm{2}} {\int}}\left\{\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {y}\right)\right\}\mid_{{y}^{\mathrm{2}} /\mathrm{4}} ^{\mathrm{1}} \:{dy} \\ $$$$=\:\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\left({y}^{\mathrm{2}} −\frac{{y}^{\mathrm{6}} }{\mathrm{16}}\right)\:{dy}\:\:\left[\:{even}\right. \\ $$$$\left.{function}\right] \\ $$$$=\:\left[\frac{\mathrm{2}}{\mathrm{3}}{y}^{\mathrm{3}} −\frac{{y}^{\mathrm{7}} }{\mathrm{112}}\:\right]_{\mathrm{9}} ^{\mathrm{2}} =\:\frac{\mathrm{16}}{\mathrm{3}}\:−\frac{\mathrm{128}}{\mathrm{112}} \\ $$$$=\frac{\mathrm{16}}{\mathrm{3}}−\frac{\mathrm{8}}{\mathrm{7}}\:=\:\frac{\mathrm{88}}{\mathrm{21}} \\ $$
