Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 103863 by mohammad17 last updated on 17/Jul/20

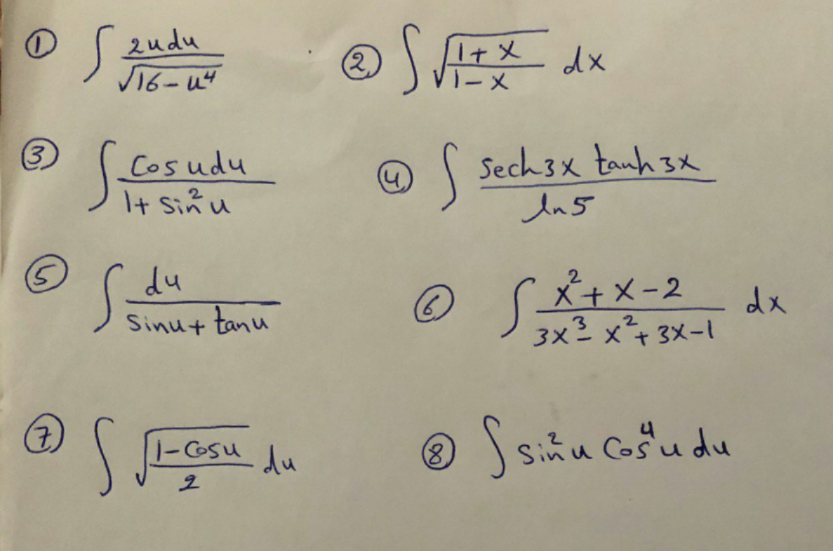
Answered by Dwaipayan Shikari last updated on 17/Jul/20

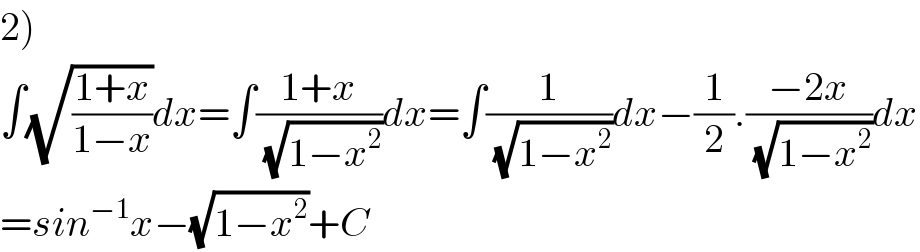
2) ∫(√((1+x)/(1−x)))dx=∫((1+x)/(√(1−x^2 )))dx=∫(1/(√(1−x^2 )))dx−(1/2).((−2x)/(√(1−x^2 )))dx =sin^(−1) x−(√(1−x^2 ))+C

$$\left.\mathrm{2}\right) \\ $$$$\int\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}{dx}=\int\frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\int\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{−\mathrm{2}{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$={sin}^{−\mathrm{1}} {x}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{C} \\ $$

Answered by Dwaipayan Shikari last updated on 17/Jul/20

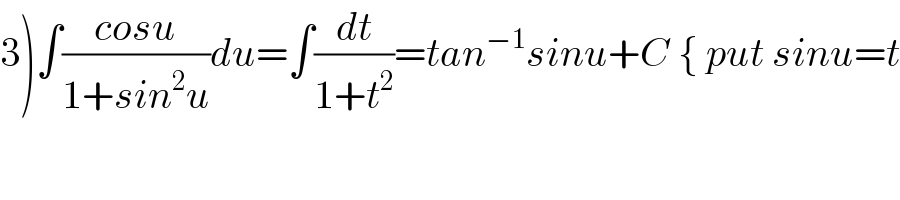
3)∫((cosu)/(1+sin^2 u))du=∫(dt/(1+t^2 ))=tan^(−1) sinu+C { put sinu=t

$$\left.\mathrm{3}\right)\int\frac{{cosu}}{\mathrm{1}+{sin}^{\mathrm{2}} {u}}{du}=\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }={tan}^{−\mathrm{1}} {sinu}+{C}\:\left\{\:{put}\:{sinu}={t}\right. \\ $$

Answered by Dwaipayan Shikari last updated on 17/Jul/20

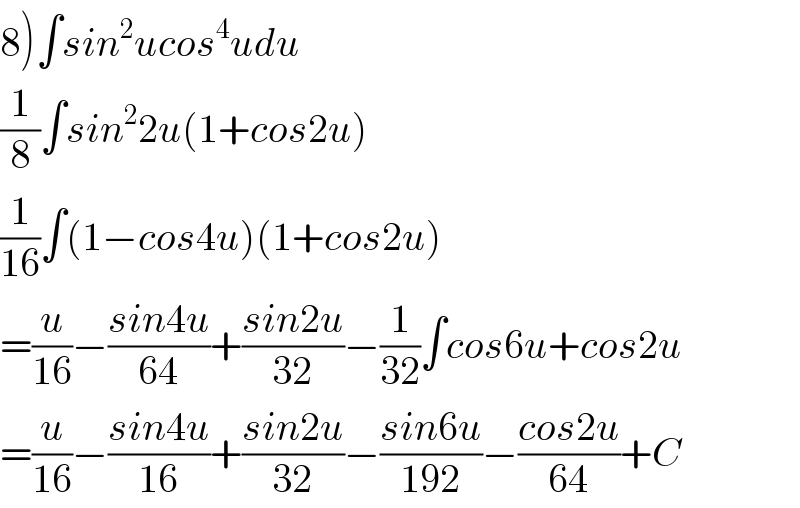
8)∫sin^2 ucos^4 udu (1/8)∫sin^2 2u(1+cos2u) (1/(16))∫(1−cos4u)(1+cos2u) =(u/(16))−((sin4u)/(64))+((sin2u)/(32))−(1/(32))∫cos6u+cos2u =(u/(16))−((sin4u)/(16))+((sin2u)/(32))−((sin6u)/(192))−((cos2u)/(64))+C

$$\left.\mathrm{8}\right)\int{sin}^{\mathrm{2}} {ucos}^{\mathrm{4}} {udu} \\ $$$$\frac{\mathrm{1}}{\mathrm{8}}\int{sin}^{\mathrm{2}} \mathrm{2}{u}\left(\mathrm{1}+{cos}\mathrm{2}{u}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\int\left(\mathrm{1}−{cos}\mathrm{4}{u}\right)\left(\mathrm{1}+{cos}\mathrm{2}{u}\right) \\ $$$$=\frac{{u}}{\mathrm{16}}−\frac{{sin}\mathrm{4}{u}}{\mathrm{64}}+\frac{{sin}\mathrm{2}{u}}{\mathrm{32}}−\frac{\mathrm{1}}{\mathrm{32}}\int{cos}\mathrm{6}{u}+{cos}\mathrm{2}{u} \\ $$$$=\frac{{u}}{\mathrm{16}}−\frac{{sin}\mathrm{4}{u}}{\mathrm{16}}+\frac{{sin}\mathrm{2}{u}}{\mathrm{32}}−\frac{{sin}\mathrm{6}{u}}{\mathrm{192}}−\frac{{cos}\mathrm{2}{u}}{\mathrm{64}}+{C} \\ $$

Answered by Dwaipayan Shikari last updated on 17/Jul/20

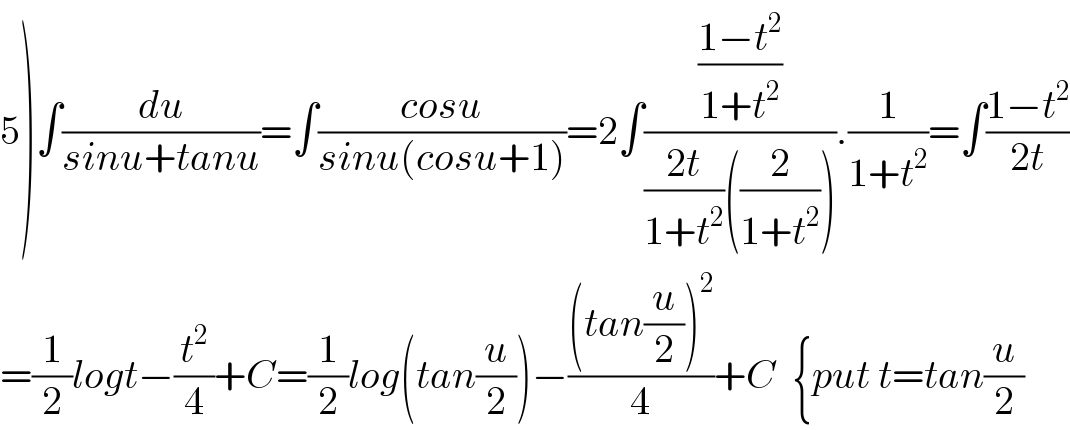
5)∫(du/(sinu+tanu))=∫((cosu)/(sinu(cosu+1)))=2∫(((1−t^2 )/(1+t^2 ))/(((2t)/(1+t^2 ))((2/(1+t^2 ))))).(1/(1+t^2 ))=∫((1−t^2 )/(2t)) =(1/2)logt−(t^2 /4)+C=(1/2)log(tan(u/2))−(((tan(u/2))^2 )/4)+C {put t=tan(u/2)

$$\left.\mathrm{5}\right)\int\frac{{du}}{{sinu}+{tanu}}=\int\frac{{cosu}}{{sinu}\left({cosu}+\mathrm{1}\right)}=\mathrm{2}\int\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\left(\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }=\int\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{logt}−\frac{{t}^{\mathrm{2}} }{\mathrm{4}}+{C}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left({tan}\frac{{u}}{\mathrm{2}}\right)−\frac{\left({tan}\frac{{u}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}}+{C}\:\:\left\{{put}\:{t}={tan}\frac{{u}}{\mathrm{2}}\right. \\ $$

Answered by mathmax by abdo last updated on 17/Jul/20

1) I =∫ ((2udu)/(√(16−u^4 ))) changement u^2 =x give 2udu =dx ⇒ I =∫ (dx/(√(16−x^2 ))) =_(x =4t) ∫ ((4dt)/(4(√(1−t^2 )))) =arcsint +C =arcsin((x/4)) +c =arcsin((u^2 /4)) +c .

$$\left.\mathrm{1}\right)\:\mathrm{I}\:=\int\:\:\frac{\mathrm{2udu}}{\sqrt{\mathrm{16}−\mathrm{u}^{\mathrm{4}} }}\:\:\mathrm{changement}\:\mathrm{u}^{\mathrm{2}} \:=\mathrm{x}\:\mathrm{give}\:\mathrm{2udu}\:=\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\sqrt{\mathrm{16}−\mathrm{x}^{\mathrm{2}} }}\:=_{\mathrm{x}\:=\mathrm{4t}} \:\:\:\:\int\:\:\frac{\mathrm{4dt}}{\mathrm{4}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:=\mathrm{arcsint}\:+\mathrm{C} \\ $$$$=\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{4}}\right)\:+\mathrm{c}\:=\mathrm{arcsin}\left(\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{4}}\right)\:+\mathrm{c}\:. \\ $$

Answered by mathmax by abdo last updated on 17/Jul/20

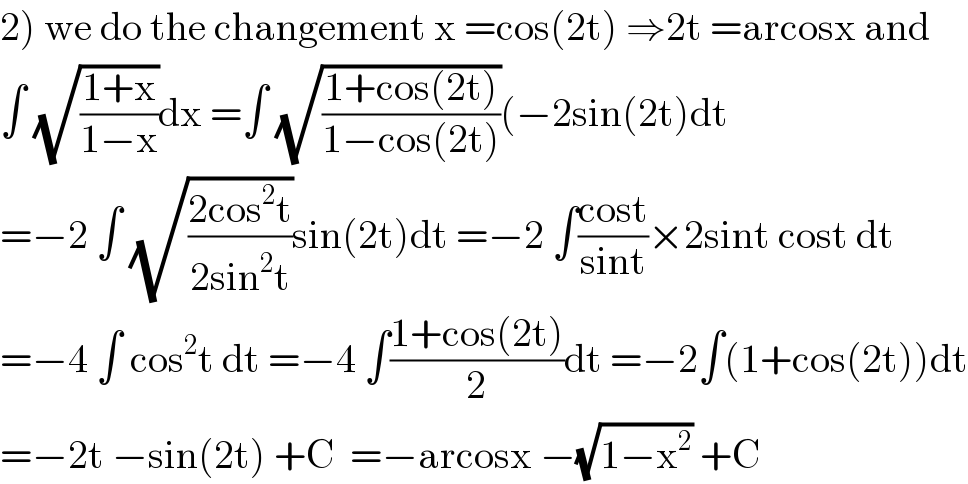
2) we do the changement x =cos(2t) ⇒2t =arcosx and ∫ (√((1+x)/(1−x)))dx =∫ (√((1+cos(2t))/(1−cos(2t))))(−2sin(2t)dt =−2 ∫ (√((2cos^2 t)/(2sin^2 t)))sin(2t)dt =−2 ∫((cost)/(sint))×2sint cost dt =−4 ∫ cos^2 t dt =−4 ∫((1+cos(2t))/2)dt =−2∫(1+cos(2t))dt =−2t −sin(2t) +C =−arcosx −(√(1−x^2 )) +C

$$\left.\mathrm{2}\right)\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{cos}\left(\mathrm{2t}\right)\:\Rightarrow\mathrm{2t}\:=\mathrm{arcosx}\:\mathrm{and} \\ $$$$\int\:\sqrt{\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\mathrm{dx}\:=\int\:\sqrt{\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{1}−\mathrm{cos}\left(\mathrm{2t}\right)}}\left(−\mathrm{2sin}\left(\mathrm{2t}\right)\mathrm{dt}\right. \\ $$$$=−\mathrm{2}\:\int\:\sqrt{\frac{\mathrm{2cos}^{\mathrm{2}} \mathrm{t}}{\mathrm{2sin}^{\mathrm{2}} \mathrm{t}}}\mathrm{sin}\left(\mathrm{2t}\right)\mathrm{dt}\:=−\mathrm{2}\:\int\frac{\mathrm{cost}}{\mathrm{sint}}×\mathrm{2sint}\:\mathrm{cost}\:\mathrm{dt} \\ $$$$=−\mathrm{4}\:\int\:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=−\mathrm{4}\:\int\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\mathrm{dt}\:=−\mathrm{2}\int\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{dt} \\ $$$$=−\mathrm{2t}\:−\mathrm{sin}\left(\mathrm{2t}\right)\:+\mathrm{C}\:\:=−\mathrm{arcosx}\:−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:+\mathrm{C} \\ $$

Answered by bemath last updated on 18/Jul/20

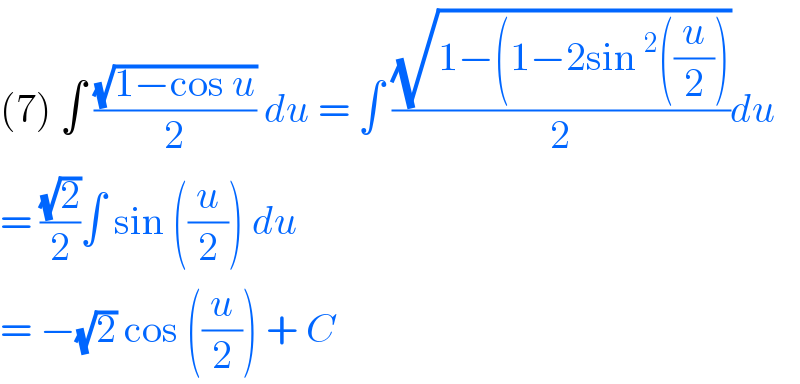
(7) ∫ ((√(1−cos u))/2) du = ∫ ((√(1−(1−2sin^2 ((u/2))))/2)du = ((√2)/2)∫ sin ((u/2)) du = −(√2) cos ((u/2)) + C

$$\left(\mathrm{7}\right)\:\int\:\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:{u}}}{\mathrm{2}}\:{du}\:=\:\int\:\frac{\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{{u}}{\mathrm{2}}\right)\right.}}{\mathrm{2}}{du} \\ $$$$=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\:\mathrm{sin}\:\left(\frac{{u}}{\mathrm{2}}\right)\:{du}\: \\ $$$$=\:−\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left(\frac{{u}}{\mathrm{2}}\right)\:+\:{C} \\ $$

Answered by mathmax by abdo last updated on 18/Jul/20

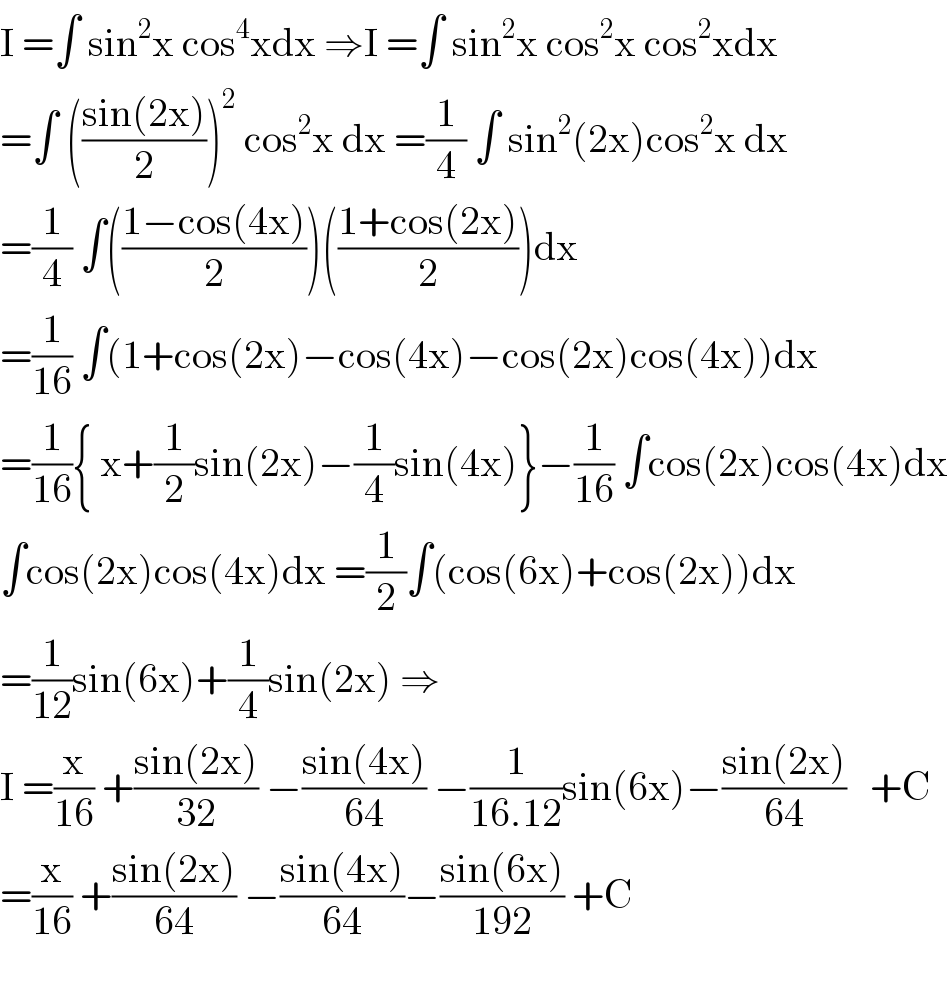
I =∫ sin^2 x cos^4 xdx ⇒I =∫ sin^2 x cos^2 x cos^2 xdx =∫ (((sin(2x))/2))^2 cos^2 x dx =(1/4) ∫ sin^2 (2x)cos^2 x dx =(1/4) ∫(((1−cos(4x))/2))(((1+cos(2x))/2))dx =(1/(16)) ∫(1+cos(2x)−cos(4x)−cos(2x)cos(4x))dx =(1/(16)){ x+(1/2)sin(2x)−(1/4)sin(4x)}−(1/(16)) ∫cos(2x)cos(4x)dx ∫cos(2x)cos(4x)dx =(1/2)∫(cos(6x)+cos(2x))dx =(1/(12))sin(6x)+(1/4)sin(2x) ⇒ I =(x/(16)) +((sin(2x))/(32)) −((sin(4x))/(64)) −(1/(16.12))sin(6x)−((sin(2x))/(64)) +C =(x/(16)) +((sin(2x))/(64)) −((sin(4x))/(64))−((sin(6x))/(192)) +C

$$\mathrm{I}\:=\int\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{cos}^{\mathrm{4}} \mathrm{xdx}\:\Rightarrow\mathrm{I}\:=\int\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{cos}^{\mathrm{2}} \mathrm{xdx} \\ $$$$=\int\:\left(\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)}{\mathrm{2}}\right)\left(\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{cos}\left(\mathrm{4x}\right)−\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{4x}\right)\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left\{\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{4x}\right)\right\}−\frac{\mathrm{1}}{\mathrm{16}}\:\int\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{dx} \\ $$$$\int\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{cos}\left(\mathrm{6x}\right)+\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\mathrm{sin}\left(\mathrm{6x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2x}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{x}}{\mathrm{16}}\:+\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{32}}\:−\frac{\mathrm{sin}\left(\mathrm{4x}\right)}{\mathrm{64}}\:−\frac{\mathrm{1}}{\mathrm{16}.\mathrm{12}}\mathrm{sin}\left(\mathrm{6x}\right)−\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{64}}\:\:\:+\mathrm{C} \\ $$$$=\frac{\mathrm{x}}{\mathrm{16}}\:+\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{64}}\:−\frac{\mathrm{sin}\left(\mathrm{4x}\right)}{\mathrm{64}}−\frac{\mathrm{sin}\left(\mathrm{6x}\right)}{\mathrm{192}}\:+\mathrm{C} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com