
Question Number 103879 by abony1303 last updated on 18/Jul/20
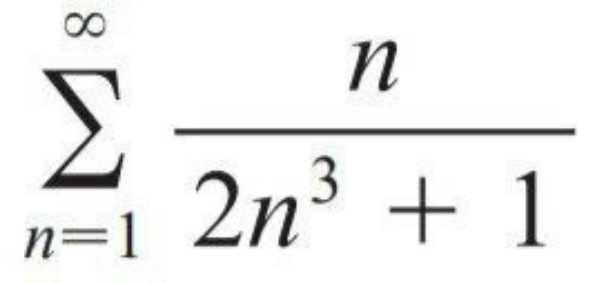
Commented by abony1303 last updated on 18/Jul/20

$$\mathrm{Please},\:\mathrm{help} \\ $$
Commented by myear last updated on 18/Jul/20
plain
Answered by Ar Brandon last updated on 18/Jul/20

$$\frac{\mathrm{n}}{\mathrm{2n}^{\mathrm{3}} +\mathrm{1}}=\frac{\mathrm{n}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{n}^{\mathrm{2}} −\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{a}}{\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}}+\frac{\mathrm{bn}+\mathrm{c}}{\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{n}^{\mathrm{2}} −\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{a}\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{n}^{\mathrm{2}} −\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}\right)+\left(\mathrm{bn}+\mathrm{c}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}\right)}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{n}^{\mathrm{2}} −\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}\right)} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{a}+\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{b}=\mathrm{0}\:,\:\mathrm{a}+\mathrm{c}=\mathrm{0}\:,\:−\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{a}+\mathrm{b}+\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{c}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{b}−\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{a}=\mathrm{1}\:\Rightarrow\:\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{a}=−\sqrt[{\mathrm{3}}]{\mathrm{2}}\Rightarrow\mathrm{a}=\frac{−\mathrm{1}}{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}\:,\:\mathrm{c}=\frac{\mathrm{1}}{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}\:,\:\mathrm{b}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{n}}{\mathrm{2n}^{\mathrm{3}} +\mathrm{1}}=\frac{−\mathrm{1}/\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}}+\frac{\mathrm{n}/\mathrm{3}+\mathrm{1}/\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{n}^{\mathrm{2}} −\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}}{\mathrm{2n}^{\mathrm{3}} +\mathrm{1}}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left\{\frac{\mathrm{n}/\mathrm{3}+\mathrm{1}/\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\sqrt[{\mathrm{3}}]{\mathrm{4}}\mathrm{n}^{\mathrm{2}} −\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}/\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\sqrt[{\mathrm{3}}]{\mathrm{2}}\mathrm{n}+\mathrm{1}}\right\} \\ $$$$ \\ $$$${Any}\:{idea}\:{to}\:{proceed}\:? \\ $$
Answered by ~blr237~ last updated on 19/Jul/20
![Let state f(z)=(z/(z^3 +a^3 )) g(z)=(π/(tan(πz))) a>0 P(fg)={−a,aw_0 ,aw_1 ,−n,n / n∈N ,w_0 =e^(i(π/3)) .....} let state points A(−in),B(−n+in),C(n+in) D(in) for n≥0 δ_n =ABCDis a rectangle (close way) and f(z)=O((1/(∣z∣^2 ))) (•) The residus theorems allows us to say ∫_δ_n f(z)g(z)dz= 2πi Σ_(x∈P(fg)) ind(δ_n ,x)Res(fg,x)=2πi(Σ_(k=0) ^n f(k) +Res(fg, aw_0 )+Res(fg,aw_1 )] because (•) prove that the first term →0 when n→∞ So S=Σ_(n=0) ^∞ f(n)= −[((aw_0 g(aw_0 ))/(3(aw_0 )^2 )) +((aw_1 g(aw_1 ))/(3(aw_1 )^2 ))] S=−(2/3) Re(((aw_0 g(aw_0 ))/((aw_0 )^2 ))) cause w_(1 ) =w_0 ^− and g(z^− )=g^− (z) S=−((2π)/(3a)) Re((1/( w_0 tan(πaw_0 )))) tan(πw_0 )= −i ((e^(i2aπw_0 ) −1)/(e^(i2πaw_0 ) +1)) and 2πaiw_0 =2iπa((1/2)+i((√3)/2))=−π(√3) +iπa tan(πw_0 )=−i ((e^(iπa) e^(−π(√3)) +1)/(e^(iπa) e^(−π(√3)) −1))=−i((e^(−2π(√3)) −1−2ie^(−π(√3)) sin(πa))/(e^(−2π(√3)) +1−2cos(πa)e^(−π(√3)) )) S=((πe^(π(√3)) )/(6a(e^(−2π(√3)) +1−2e^(−π(√3)) cos(πa)))) Re( (((√3)+i)/(sh(π(√3))+isin(πa)))) S=((πe^(2π(√3)) )/(12a(ch(π(√3))−cos(πa))) ×(((√3) sh(π(√3))−sin(πa))/(sh^2 (π(√3))+sin^2 (πa))) Finally S(a)= Σ_(n=1) ^∞ (n/(n^3 + a^3 )) = ((π(√3)e^(2π(√3)) (sh(π(√3))−sin(πa)))/(12a(ch(π(√3))−cos(πa))(sh^2 (π(√3))+sin^2 (πa)))) a>0 Let deduce your by (1/2) S(^3 (√2)) .](Q104033.png)
$${Let}\:{state}\:\:{f}\left({z}\right)=\frac{{z}}{{z}^{\mathrm{3}} +{a}^{\mathrm{3}} }\:\:{g}\left({z}\right)=\frac{\pi}{{tan}\left(\pi{z}\right)}\:\:\:\:\:{a}>\mathrm{0} \\ $$$${P}\left({fg}\right)=\left\{−{a},{aw}_{\mathrm{0}} ,{aw}_{\mathrm{1}} ,−{n},{n}\:/\:\:\:\:{n}\in\mathbb{N}\:,{w}_{\mathrm{0}} ={e}^{{i}\frac{\pi}{\mathrm{3}}} .....\right\} \\ $$$${let}\:{state}\:\:\:{points}\:{A}\left(−{in}\right),{B}\left(−{n}+{in}\right),{C}\left({n}+{in}\right)\:{D}\left({in}\right)\:\:{for}\:{n}\geqslant\mathrm{0} \\ $$$$\delta_{{n}} ={ABCDis}\:{a}\:{rectangle}\:\left({close}\:{way}\right)\:{and}\:\:\:{f}\left({z}\right)={O}\left(\frac{\mathrm{1}}{\mid{z}\mid^{\mathrm{2}} }\right)\:\:\left(\bullet\right) \\ $$$${The}\:{residus}\:{theorems}\:{allows}\:{us}\:{to}\:{say} \\ $$$$\int_{\delta_{{n}} } {f}\left({z}\right){g}\left({z}\right){dz}=\:\mathrm{2}\pi{i}\:\underset{{x}\in{P}\left({fg}\right)} {\sum}{ind}\left(\delta_{{n}} ,{x}\right){Res}\left({fg},{x}\right)=\mathrm{2}\pi{i}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{f}\left({k}\right)\:+{Res}\left({fg},\:{aw}_{\mathrm{0}} \right)+{Res}\left({fg},{aw}_{\mathrm{1}} \right)\right]\:\:\:{because}\: \\ $$$$\left(\bullet\right)\:{prove}\:{that}\:\:{the}\:{first}\:{term}\:\rightarrow\mathrm{0}\:{when}\:{n}\rightarrow\infty\: \\ $$$${So}\:\:{S}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{f}\left({n}\right)=\:−\left[\frac{{aw}_{\mathrm{0}} {g}\left({aw}_{\mathrm{0}} \right)}{\mathrm{3}\left({aw}_{\mathrm{0}} \right)^{\mathrm{2}} }\:+\frac{{aw}_{\mathrm{1}} {g}\left({aw}_{\mathrm{1}} \right)}{\mathrm{3}\left({aw}_{\mathrm{1}} \right)^{\mathrm{2}} }\right] \\ $$$${S}=−\frac{\mathrm{2}}{\mathrm{3}}\:{Re}\left(\frac{{aw}_{\mathrm{0}} {g}\left({aw}_{\mathrm{0}} \right)}{\left({aw}_{\mathrm{0}} \right)^{\mathrm{2}} }\right)\:\:\:{cause}\:\:{w}_{\mathrm{1}\:} =\overset{−} {{w}}_{\mathrm{0}} \:\:\:{and}\:\:{g}\left(\overset{−} {{z}}\right)=\overset{−} {{g}}\left({z}\right) \\ $$$${S}=−\frac{\mathrm{2}\pi}{\mathrm{3}{a}}\:{Re}\left(\frac{\mathrm{1}}{\:\:\:{w}_{\mathrm{0}} {tan}\left(\pi{aw}_{\mathrm{0}} \right)}\right)\:\:\:\:\:\:\: \\ $$$${tan}\left(\pi{w}_{\mathrm{0}} \right)=\:\:−{i}\:\frac{{e}^{{i}\mathrm{2}{a}\pi{w}_{\mathrm{0}} } −\mathrm{1}}{{e}^{{i}\mathrm{2}\pi{aw}_{\mathrm{0}} } +\mathrm{1}}\:\:\:{and}\:\mathrm{2}\pi{aiw}_{\mathrm{0}} =\mathrm{2}{i}\pi{a}\left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=−\pi\sqrt{\mathrm{3}}\:+{i}\pi{a} \\ $$$${tan}\left(\pi{w}_{\mathrm{0}} \right)=−{i}\:\frac{{e}^{{i}\pi{a}} {e}^{−\pi\sqrt{\mathrm{3}}} +\mathrm{1}}{{e}^{{i}\pi{a}} {e}^{−\pi\sqrt{\mathrm{3}}} −\mathrm{1}}=−{i}\frac{{e}^{−\mathrm{2}\pi\sqrt{\mathrm{3}}} −\mathrm{1}−\mathrm{2}{ie}^{−\pi\sqrt{\mathrm{3}}} {sin}\left(\pi{a}\right)}{{e}^{−\mathrm{2}\pi\sqrt{\mathrm{3}}} +\mathrm{1}−\mathrm{2}{cos}\left(\pi{a}\right){e}^{−\pi\sqrt{\mathrm{3}}} } \\ $$$${S}=\frac{\pi{e}^{\pi\sqrt{\mathrm{3}}} }{\mathrm{6}{a}\left({e}^{−\mathrm{2}\pi\sqrt{\mathrm{3}}} +\mathrm{1}−\mathrm{2}{e}^{−\pi\sqrt{\mathrm{3}}} {cos}\left(\pi{a}\right)\right)}\:\:\:{Re}\left(\:\frac{\sqrt{\mathrm{3}}+{i}}{{sh}\left(\pi\sqrt{\mathrm{3}}\right)+{isin}\left(\pi{a}\right)}\right) \\ $$$${S}=\frac{\pi{e}^{\mathrm{2}\pi\sqrt{\mathrm{3}}} }{\mathrm{12}{a}\left({ch}\left(\pi\sqrt{\mathrm{3}}\right)−{cos}\left(\pi{a}\right)\right.}\:×\frac{\sqrt{\mathrm{3}}\:{sh}\left(\pi\sqrt{\mathrm{3}}\right)−{sin}\left(\pi{a}\right)}{{sh}^{\mathrm{2}} \left(\pi\sqrt{\mathrm{3}}\right)+{sin}^{\mathrm{2}} \left(\pi{a}\right)}\:\:\:\: \\ $$$$\:\:\:{Finally}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}\left({a}\right)=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\frac{{n}}{{n}^{\mathrm{3}} +\:{a}^{\mathrm{3}} }\:=\:\frac{\pi\sqrt{\mathrm{3}}{e}^{\mathrm{2}\pi\sqrt{\mathrm{3}}} \left({sh}\left(\pi\sqrt{\mathrm{3}}\right)−{sin}\left(\pi{a}\right)\right)}{\mathrm{12}{a}\left({ch}\left(\pi\sqrt{\mathrm{3}}\right)−{cos}\left(\pi{a}\right)\right)\left({sh}^{\mathrm{2}} \left(\pi\sqrt{\mathrm{3}}\right)+{sin}^{\mathrm{2}} \left(\pi{a}\right)\right)}\:\:\:\:\:\:{a}>\mathrm{0} \\ $$$$ \\ $$$${Let}\:\:\:{deduce}\:{your}\:{by}\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:{S}\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)\:.\:\: \\ $$
