Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 103888 by mr W last updated on 18/Jul/20

find all such numbers: if we make its last digit, say k, as its first digit, the number becomes k times large as before. (□□...□k)→(k□□...□)=k×(□□...□k)

$${find}\:{all}\:{such}\:{numbers}: \\ $$$${if}\:{we}\:{make}\:{its}\:{last}\:{digit},\:{say}\:{k},\:{as}\:{its} \\ $$$${first}\:{digit},\:{the}\:{number}\:{becomes}\:{k} \\ $$$${times}\:{large}\:{as}\:{before}. \\ $$$$\left(\Box\Box...\Box{k}\right)\rightarrow\left({k}\Box\Box...\Box\right)={k}×\left(\Box\Box...\Box{k}\right) \\ $$

Answered by MAB last updated on 18/Jul/20

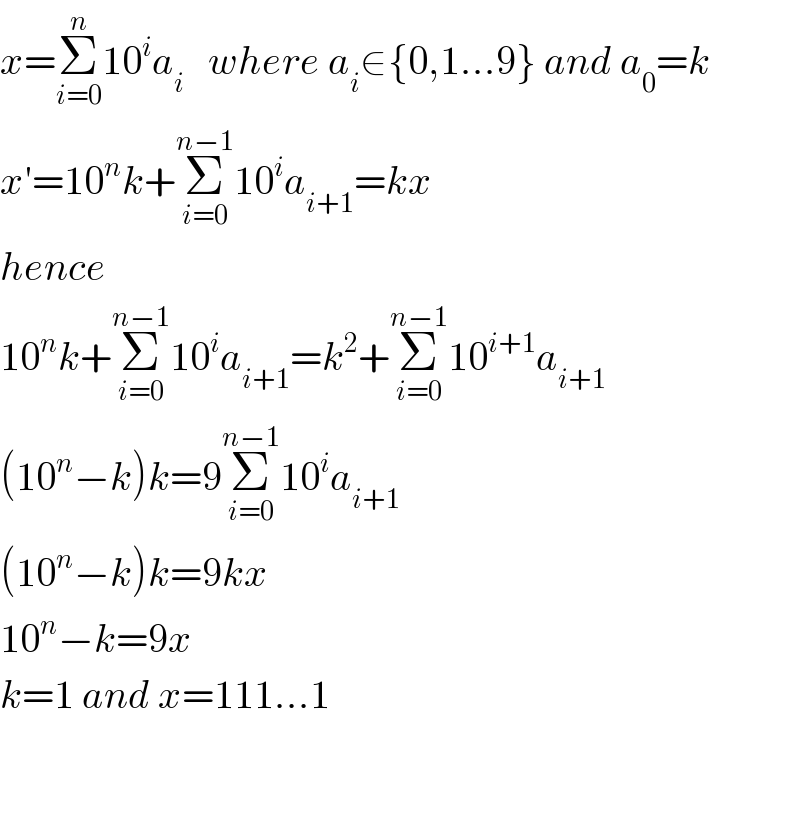
x=Σ_(i=0) ^n 10^i a_i where a_i ∈{0,1...9} and a_0 =k x′=10^n k+Σ_(i=0) ^(n−1) 10^i a_(i+1) =kx hence 10^n k+Σ_(i=0) ^(n−1) 10^i a_(i+1) =k^2 +Σ_(i=0) ^(n−1) 10^(i+1) a_(i+1) (10^n −k)k=9Σ_(i=0) ^(n−1) 10^i a_(i+1) (10^n −k)k=9kx 10^n −k=9x k=1 and x=111...1

$${x}=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{10}^{{i}} {a}_{{i}} \:\:\:{where}\:{a}_{{i}} \in\left\{\mathrm{0},\mathrm{1}...\mathrm{9}\right\}\:{and}\:{a}_{\mathrm{0}} ={k} \\ $$$${x}'=\mathrm{10}^{{n}} {k}+\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{10}^{{i}} {a}_{{i}+\mathrm{1}} ={kx} \\ $$$${hence} \\ $$$$\mathrm{10}^{{n}} {k}+\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{10}^{{i}} {a}_{{i}+\mathrm{1}} ={k}^{\mathrm{2}} +\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{10}^{{i}+\mathrm{1}} {a}_{{i}+\mathrm{1}} \\ $$$$\left(\mathrm{10}^{{n}} −{k}\right){k}=\mathrm{9}\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{10}^{{i}} {a}_{{i}+\mathrm{1}} \\ $$$$\left(\mathrm{10}^{{n}} −{k}\right){k}=\mathrm{9}{kx} \\ $$$$\mathrm{10}^{{n}} −{k}=\mathrm{9}{x} \\ $$$${k}=\mathrm{1}\:{and}\:{x}=\mathrm{111}...\mathrm{1} \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 18/Jul/20

thanks sir!

$${thanks}\:{sir}! \\ $$

Answered by mr W last updated on 18/Jul/20

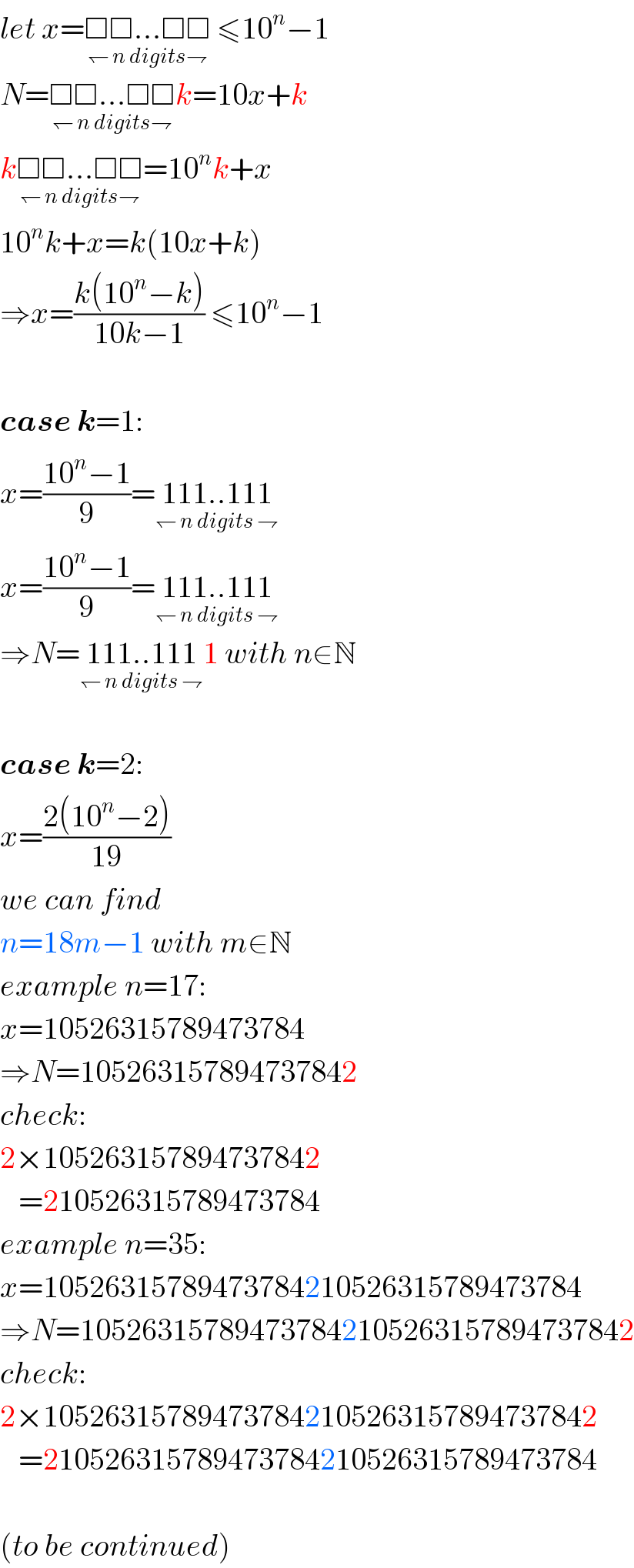
let x=□□...□□_(↽ n digits⇁) ≤10^n −1 N=□□...□□_(↽ n digits⇁) k=10x+k k□□...□□_(↽ n digits⇁) =10^n k+x 10^n k+x=k(10x+k) ⇒x=((k(10^n −k))/(10k−1)) ≤10^n −1 case k=1: x=((10^n −1)/9)=111..111_(↽ n digits ⇁) x=((10^n −1)/9)=111..111_(↽ n digits ⇁) ⇒N=111..111_(↽ n digits ⇁) 1 with n∈N case k=2: x=((2(10^n −2))/(19)) we can find n=18m−1 with m∈N example n=17: x=10526315789473784 ⇒N=105263157894737842 check: 2×105263157894737842 =210526315789473784 example n=35: x=10526315789473784210526315789473784 ⇒N=105263157894737842105263157894737842 check: 2×105263157894737842105263157894737842 =210526315789473784210526315789473784 (to be continued)

$${let}\:{x}=\underset{\leftharpoondown\:{n}\:{digits}\rightharpoondown} {\Box\Box...\Box\Box}\:\leqslant\mathrm{10}^{{n}} −\mathrm{1} \\ $$$${N}=\underset{\leftharpoondown\:{n}\:{digits}\rightharpoondown} {\Box\Box...\Box\Box}{k}=\mathrm{10}{x}+{k} \\ $$$${k}\underset{\leftharpoondown\:{n}\:{digits}\rightharpoondown} {\Box\Box...\Box\Box}=\mathrm{10}^{{n}} {k}+{x} \\ $$$$\mathrm{10}^{{n}} {k}+{x}={k}\left(\mathrm{10}{x}+{k}\right) \\ $$$$\Rightarrow{x}=\frac{{k}\left(\mathrm{10}^{{n}} −{k}\right)}{\mathrm{10}{k}−\mathrm{1}}\:\leqslant\mathrm{10}^{{n}} −\mathrm{1} \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\boldsymbol{{k}}=\mathrm{1}: \\ $$$${x}=\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{9}}=\underset{\leftharpoondown\:{n}\:{digits}\:\rightharpoondown} {\mathrm{111}..\mathrm{111}} \\ $$$${x}=\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{9}}=\underset{\leftharpoondown\:{n}\:{digits}\:\rightharpoondown} {\mathrm{111}..\mathrm{111}} \\ $$$$\Rightarrow{N}=\underset{\leftharpoondown\:{n}\:{digits}\:\rightharpoondown} {\mathrm{111}..\mathrm{111}1}\:{with}\:{n}\in\mathbb{N} \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\boldsymbol{{k}}=\mathrm{2}: \\ $$$${x}=\frac{\mathrm{2}\left(\mathrm{10}^{{n}} −\mathrm{2}\right)}{\mathrm{19}} \\ $$$${we}\:{can}\:{find} \\ $$$${n}=\mathrm{18}{m}−\mathrm{1}\:{with}\:{m}\in\mathbb{N} \\ $$$${example}\:{n}=\mathrm{17}: \\ $$$${x}=\mathrm{10526315789473784} \\ $$$$\Rightarrow{N}=\mathrm{105263157894737842} \\ $$$${check}: \\ $$$$\mathrm{2}×\mathrm{105263157894737842} \\ $$$$\:\:\:=\mathrm{210526315789473784} \\ $$$${example}\:{n}=\mathrm{35}: \\ $$$${x}=\mathrm{10526315789473784210526315789473784} \\ $$$$\Rightarrow{N}=\mathrm{105263157894737842105263157894737842} \\ $$$${check}: \\ $$$$\mathrm{2}×\mathrm{105263157894737842105263157894737842} \\ $$$$\:\:\:=\mathrm{210526315789473784210526315789473784} \\ $$$$ \\ $$$$\left({to}\:{be}\:{continued}\right) \\ $$

Commented by mr W last updated on 18/Jul/20

case k=3: here we′ll try an other way to find the number x. note: in following the digits of the number are displayed inversely, i.e. the last digit is the left most. 39731427155698602685728443013 ×3 97314271556986026857284430139 ∣← last digit first digit →∣ ⇒ x=103448275862068965517241379 ⇒N=1034482758620689655172413793 check: 3×1034482758620689655172413793 =3103448275862068965517241379 we see the digits of number N may be repeated any times. so we have infinite numbers which satisfy the requirement.

$$\boldsymbol{{case}}\:\boldsymbol{{k}}=\mathrm{3}: \\ $$$${here}\:{we}'{ll}\:{try}\:{an}\:{other}\:{way}\:{to}\:{find} \\ $$$${the}\:{number}\:{x}. \\ $$$${note}:\:{in}\:{following}\:{the}\:{digits}\:{of}\:{the} \\ $$$${number}\:{are}\:{displayed}\:{inversely},\:{i}.{e}. \\ $$$${the}\:{last}\:{digit}\:{is}\:{the}\:{left}\:{most}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{39731427155698602685728443013} \\ $$$$×\mathrm{3}\:\:\:\mathrm{97314271556986026857284430139} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mid\leftarrow\:{last}\:{digit}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{first}\:{digit}\:\rightarrow\mid \\ $$$$\Rightarrow\:{x}=\mathrm{103448275862068965517241379} \\ $$$$\Rightarrow{N}=\mathrm{1034482758620689655172413793} \\ $$$${check}: \\ $$$$\mathrm{3}×\mathrm{1034482758620689655172413793} \\ $$$$\:\:\:=\mathrm{3103448275862068965517241379} \\ $$$${we}\:{see}\:{the}\:{digits}\:{of}\:{number}\:{N}\:{may}\:{be} \\ $$$${repeated}\:{any}\:{times}.\:{so}\:{we}\:{have} \\ $$$${infinite}\:{numbers}\:{which}\:{satisfy}\:{the} \\ $$$${requirement}. \\ $$

Commented by mr W last updated on 18/Jul/20

case k=4: using the same method as before, 4652014 ×4 6520146 ⇒ x=10256 ⇒N=102564 check: 4×102564 =410256 similarly the digits of N may be repeated any times. for example N=102564102564102564

$$\boldsymbol{{case}}\:\boldsymbol{{k}}=\mathrm{4}: \\ $$$${using}\:{the}\:{same}\:{method}\:{as}\:{before}, \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{4652014} \\ $$$$×\mathrm{4}\:\:\mathrm{6520146} \\ $$$$\Rightarrow\:{x}=\mathrm{10256} \\ $$$$\Rightarrow{N}=\mathrm{102564} \\ $$$${check}: \\ $$$$\mathrm{4}×\mathrm{102564} \\ $$$$\:\:\:=\mathrm{410256} \\ $$$${similarly}\:{the}\:{digits}\:{of}\:{N}\:{may}\:{be} \\ $$$${repeated}\:{any}\:{times}.\:{for}\:{example} \\ $$$${N}=\mathrm{102564102564102564} \\ $$

Commented by mr W last updated on 18/Jul/20

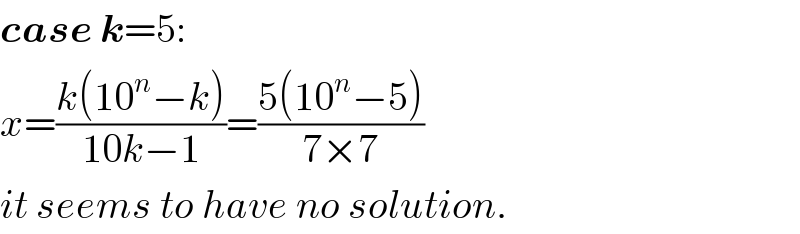
case k=5: x=((k(10^n −k))/(10k−1))=((5(10^n −5))/(7×7)) it seems to have no solution.

$$\boldsymbol{{case}}\:\boldsymbol{{k}}=\mathrm{5}: \\ $$$${x}=\frac{{k}\left(\mathrm{10}^{{n}} −{k}\right)}{\mathrm{10}{k}−\mathrm{1}}=\frac{\mathrm{5}\left(\mathrm{10}^{{n}} −\mathrm{5}\right)}{\mathrm{7}×\mathrm{7}} \\ $$$${it}\:{seems}\:{to}\:{have}\:{no}\:{solution}. \\ $$

Commented by mr W last updated on 19/Jul/20

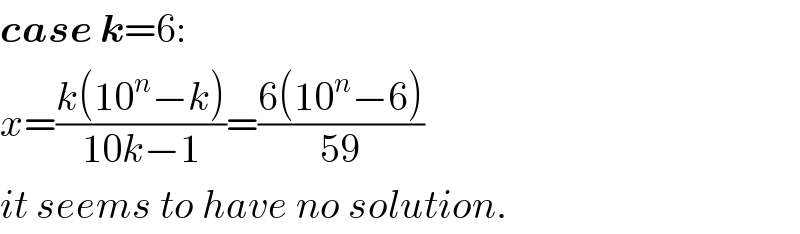
case k=6: x=((k(10^n −k))/(10k−1))=((6(10^n −6))/(59)) it seems to have no solution.

$$\boldsymbol{{case}}\:\boldsymbol{{k}}=\mathrm{6}: \\ $$$${x}=\frac{{k}\left(\mathrm{10}^{{n}} −{k}\right)}{\mathrm{10}{k}−\mathrm{1}}=\frac{\mathrm{6}\left(\mathrm{10}^{{n}} −\mathrm{6}\right)}{\mathrm{59}} \\ $$$${it}\:{seems}\:{to}\:{have}\:{no}\:{solution}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com