Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 103894 by Study last updated on 18/Jul/20

(d/(d((d/dx)sinx)))∙sinx=?

$$\frac{{d}}{{d}\left(\frac{{d}}{{dx}}{sinx}\right)}\centerdot{sinx}=? \\ $$

Answered by 1549442205 last updated on 18/Jul/20

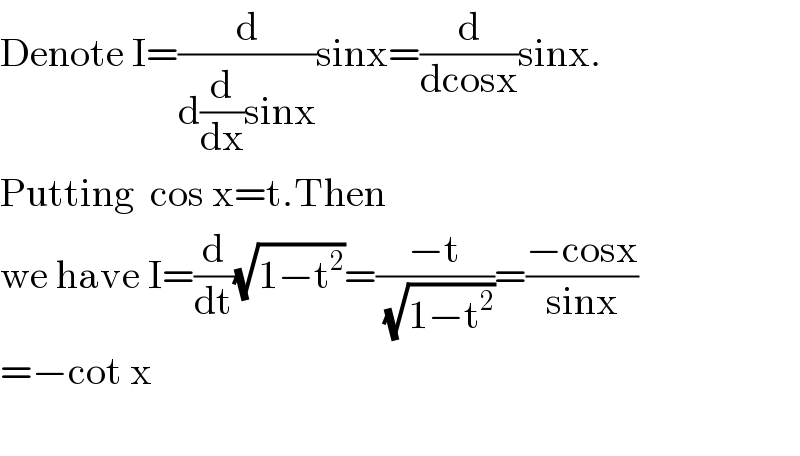
Denote I=(d/(d(d/dx)sinx))sinx=(d/(dcosx))sinx. Putting cos x=t.Then we have I=(d/dt)(√(1−t^2 ))=((−t)/(√(1−t^2 )))=((−cosx)/(sinx)) =−cot x

$$\mathrm{Denote}\:\mathrm{I}=\frac{\mathrm{d}}{\mathrm{d}\frac{\mathrm{d}}{\mathrm{dx}}\mathrm{sinx}}\mathrm{sinx}=\frac{\mathrm{d}}{\mathrm{dcosx}}\mathrm{sinx}. \\ $$$$\mathrm{Putting}\:\:\mathrm{cos}\:\mathrm{x}=\mathrm{t}.\mathrm{Then} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{I}=\frac{\mathrm{d}}{\mathrm{dt}}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }=\frac{−\mathrm{t}}{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}=\frac{−\mathrm{cosx}}{\mathrm{sinx}} \\ $$$$=−\mathrm{cot}\:\mathrm{x} \\ $$$$ \\ $$

Answered by MAB last updated on 18/Jul/20

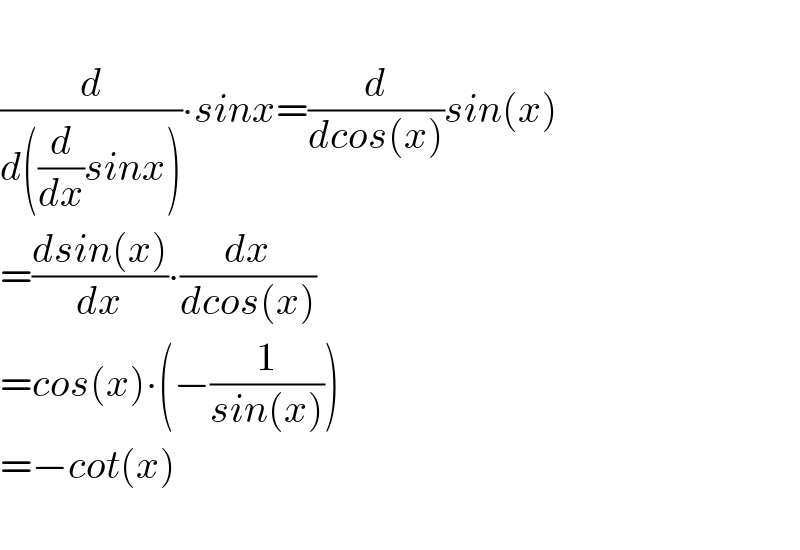
(d/(d((d/dx)sinx)))∙sinx=(d/(dcos(x)))sin(x) =((dsin(x))/dx)∙(dx/(dcos(x))) =cos(x)∙(−(1/(sin(x)))) =−cot(x)

$$ \\ $$$$\frac{{d}}{{d}\left(\frac{{d}}{{dx}}{sinx}\right)}\centerdot{sinx}=\frac{{d}}{{dcos}\left({x}\right)}{sin}\left({x}\right) \\ $$$$=\frac{{dsin}\left({x}\right)}{{dx}}\centerdot\frac{{dx}}{{dcos}\left({x}\right)} \\ $$$$={cos}\left({x}\right)\centerdot\left(−\frac{\mathrm{1}}{{sin}\left({x}\right)}\right) \\ $$$$=−{cot}\left({x}\right) \\ $$$$ \\ $$

Commented by Study last updated on 18/Jul/20

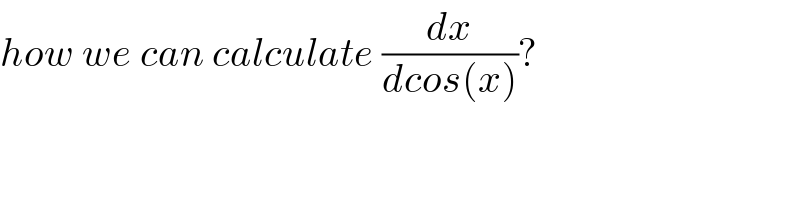
how we can calculate (dx/(dcos(x)))?

$${how}\:{we}\:{can}\:{calculate}\:\frac{{dx}}{{dcos}\left({x}\right)}? \\ $$

Commented by bobhans last updated on 18/Jul/20

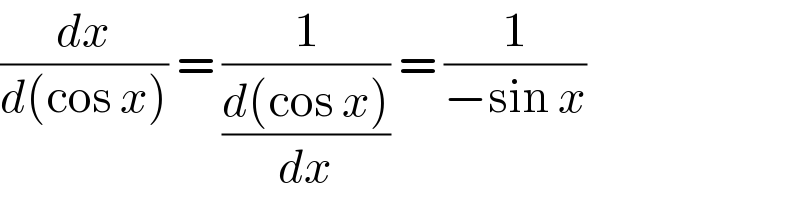
(dx/(d(cos x))) = (1/((d(cos x))/dx)) = (1/(−sin x))

$$\frac{{dx}}{{d}\left(\mathrm{cos}\:{x}\right)}\:=\:\frac{\mathrm{1}}{\frac{{d}\left(\mathrm{cos}\:{x}\right)}{{dx}}}\:=\:\frac{\mathrm{1}}{−\mathrm{sin}\:{x}} \\ $$

Answered by bobhans last updated on 18/Jul/20

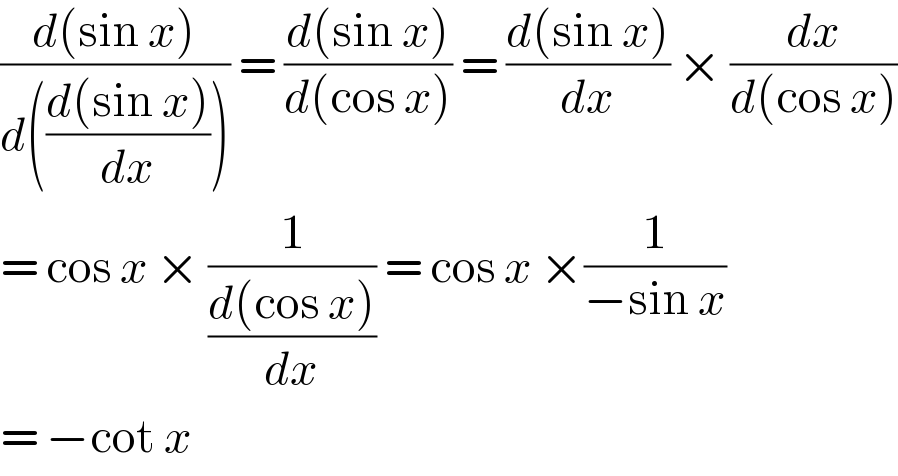
((d(sin x))/(d(((d(sin x))/dx)))) = ((d(sin x))/(d(cos x))) = ((d(sin x))/dx) × (dx/(d(cos x))) = cos x × (1/((d(cos x))/dx)) = cos x ×(1/(−sin x)) = −cot x

$$\frac{{d}\left(\mathrm{sin}\:{x}\right)}{{d}\left(\frac{{d}\left(\mathrm{sin}\:{x}\right)}{{dx}}\right)}\:=\:\frac{{d}\left(\mathrm{sin}\:{x}\right)}{{d}\left(\mathrm{cos}\:{x}\right)}\:=\:\frac{{d}\left(\mathrm{sin}\:{x}\right)}{{dx}}\:×\:\frac{{dx}}{{d}\left(\mathrm{cos}\:{x}\right)} \\ $$$$=\:\mathrm{cos}\:{x}\:×\:\frac{\mathrm{1}}{\frac{{d}\left(\mathrm{cos}\:{x}\right)}{{dx}}}\:=\:\mathrm{cos}\:{x}\:×\frac{\mathrm{1}}{−\mathrm{sin}\:{x}} \\ $$$$=\:−\mathrm{cot}\:{x}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com