Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 103908 by bobhans last updated on 18/Jul/20

Find the least positive integer n for which there exists a set { s_1 ,s_2 ,s_3 ,...,s_n } consisting of n distinct positive integers such that (1−(1/s_1 ))(1−(1/s_2 ))(1−(1/s_3 ))...(1−(1/s_n )) = ((51)/(2010)) .

$${Find}\:{the}\:{least}\:{positive}\:{integer}\:{n}\:{for} \\ $$$${which}\:{there}\:{exists}\:{a}\:{set}\:\left\{\:{s}_{\mathrm{1}} ,{s}_{\mathrm{2}} ,{s}_{\mathrm{3}} ,...,{s}_{{n}} \:\right\} \\ $$$${consisting}\:{of}\:{n}\:{distinct}\:{positive}\:{integers} \\ $$$${such}\:{that}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{1}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{3}} }\right)...\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{{n}} }\right) \\ $$$$=\:\frac{\mathrm{51}}{\mathrm{2010}}\:. \\ $$

Commented by Rasheed.Sindhi last updated on 18/Jul/20

((51)/(2010))=((17)/(670))

$$\frac{\mathrm{51}}{\mathrm{2010}}=\frac{\mathrm{17}}{\mathrm{670}} \\ $$

Commented by bobhans last updated on 18/Jul/20

for n =?? sir

$${for}\:{n}\:=??\:{sir} \\ $$

Answered by mr W last updated on 18/Jul/20

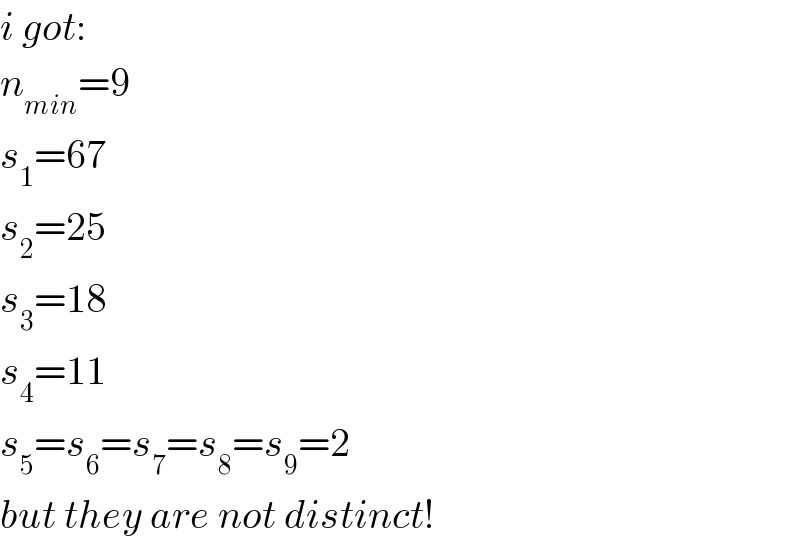
i got: n_(min) =9 s_1 =67 s_2 =25 s_3 =18 s_4 =11 s_5 =s_6 =s_7 =s_8 =s_9 =2 but they are not distinct!

$${i}\:{got}: \\ $$$${n}_{{min}} =\mathrm{9} \\ $$$${s}_{\mathrm{1}} =\mathrm{67} \\ $$$${s}_{\mathrm{2}} =\mathrm{25} \\ $$$${s}_{\mathrm{3}} =\mathrm{18} \\ $$$${s}_{\mathrm{4}} =\mathrm{11} \\ $$$${s}_{\mathrm{5}} ={s}_{\mathrm{6}} ={s}_{\mathrm{7}} ={s}_{\mathrm{8}} ={s}_{\mathrm{9}} =\mathrm{2} \\ $$$${but}\:{they}\:{are}\:{not}\:{distinct}! \\ $$

Answered by john santu last updated on 18/Jul/20

suppose that for n there exist the desired numbers; we may assumse that s_1 <s_2 <s_3 <...<s_n . surely s_1 >1 since otherwise 1−(1/s_1 ) = 0 . so we have 2≤s_1 ≤s_2 −1≤...≤s_n −(n−1), hence s_i ≥i +1 for each i=1,2,...,n. Therefore ((51)/(2010)) = (1−(1/s_1 ))(1−(1/s_2 ))...(1−(1/s_n )) ≥ (1−(1/2))(1−(1/3))...(1−(1/(n+1)))=(1/2).(2/3).(3/4)...(n/(n+2)) which implies n+1 ≥ ((2010)/(51))=((670)/(17))>39 so n≥ 39. Now we are left to show that n=39 fits. consider the set { 2,3,4,...33,34,...,67 } which contains exactly 39 numbers. we have (1/2).(2/3)...((32)/(33)).((33)/(34))...((39)/(40)).((66)/(67)) = (1/(33)).((34)/(40)).((66)/(67)) = ((17)/(670)) = ((51)/(2010)). hence for n = 39 there exist a desired example . (JS ⊛)

$${suppose}\:{that}\:{for}\:{n}\:{there}\:{exist} \\ $$$${the}\:{desired}\:{numbers};\:{we}\:{may} \\ $$$${assumse}\:{that}\:{s}_{\mathrm{1}} <{s}_{\mathrm{2}} <{s}_{\mathrm{3}} <...<{s}_{{n}} . \\ $$$${surely}\:{s}_{\mathrm{1}} >\mathrm{1}\:{since}\:{otherwise} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{1}} }\:=\:\mathrm{0}\:.\:{so}\:{we}\:{have}\:\mathrm{2}\leqslant{s}_{\mathrm{1}} \leqslant{s}_{\mathrm{2}} −\mathrm{1}\leqslant...\leqslant{s}_{{n}} −\left({n}−\mathrm{1}\right), \\ $$$${hence}\:{s}_{{i}} \:\geqslant{i}\:+\mathrm{1}\:{for}\:{each} \\ $$$${i}=\mathrm{1},\mathrm{2},...,{n}.\:{Therefore}\:\frac{\mathrm{51}}{\mathrm{2010}}\:= \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{1}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{2}} }\right)...\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{{n}} }\right)\:\geqslant\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)...\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{3}}{\mathrm{4}}...\frac{{n}}{{n}+\mathrm{2}} \\ $$$${which}\:{implies}\:{n}+\mathrm{1}\:\geqslant\:\frac{\mathrm{2010}}{\mathrm{51}}=\frac{\mathrm{670}}{\mathrm{17}}>\mathrm{39} \\ $$$${so}\:{n}\geqslant\:\mathrm{39}.\:{Now}\:{we}\:{are}\:{left}\:{to} \\ $$$${show}\:{that}\:{n}=\mathrm{39}\:{fits}.\:{consider} \\ $$$${the}\:{set}\:\left\{\:\mathrm{2},\mathrm{3},\mathrm{4},...\mathrm{33},\mathrm{34},...,\mathrm{67}\:\right\} \\ $$$${which}\:{contains}\:{exactly}\:\mathrm{39} \\ $$$${numbers}.\:{we}\:{have}\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}...\frac{\mathrm{32}}{\mathrm{33}}.\frac{\mathrm{33}}{\mathrm{34}}...\frac{\mathrm{39}}{\mathrm{40}}.\frac{\mathrm{66}}{\mathrm{67}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{33}}.\frac{\mathrm{34}}{\mathrm{40}}.\frac{\mathrm{66}}{\mathrm{67}}\:=\:\frac{\mathrm{17}}{\mathrm{670}}\:=\:\frac{\mathrm{51}}{\mathrm{2010}}. \\ $$$${hence}\:{for}\:{n}\:=\:\mathrm{39}\:{there}\:{exist}\:{a} \\ $$$${desired}\:{example}\:.\:\left({JS}\:\circledast\right)\: \\ $$

Commented by bobhans last updated on 18/Jul/20

thank you

$${thank}\:{you} \\ $$

Commented by mr W last updated on 18/Jul/20

very nice!

$${very}\:{nice}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com