Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 103931 by bemath last updated on 18/Jul/20

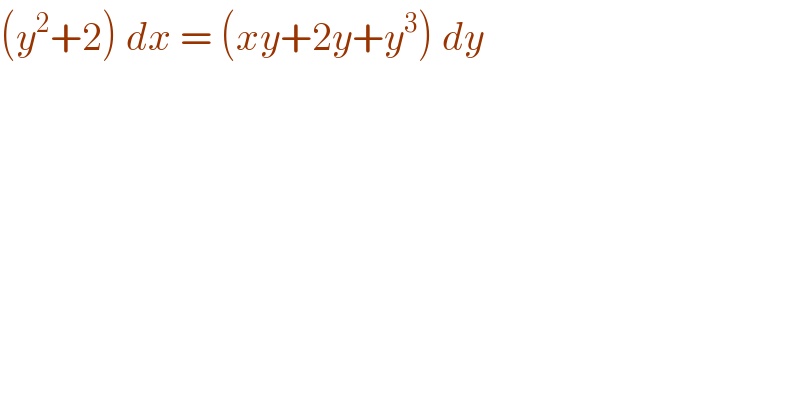
(y^2 +2) dx = (xy+2y+y^3 ) dy

$$\left({y}^{\mathrm{2}} +\mathrm{2}\right)\:{dx}\:=\:\left({xy}+\mathrm{2}{y}+{y}^{\mathrm{3}} \right)\:{dy} \\ $$

Answered by bobhans last updated on 18/Jul/20

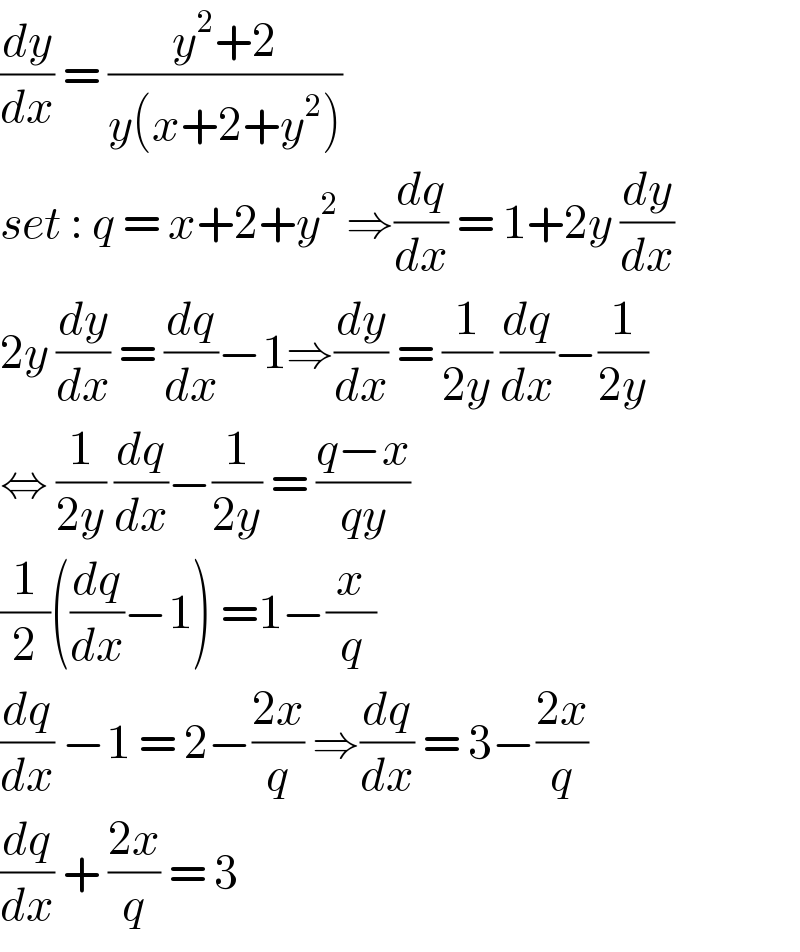
(dy/dx) = ((y^2 +2)/(y(x+2+y^2 ))) set : q = x+2+y^2 ⇒(dq/dx) = 1+2y (dy/dx) 2y (dy/dx) = (dq/dx)−1⇒(dy/dx) = (1/(2y)) (dq/dx)−(1/(2y)) ⇔ (1/(2y)) (dq/dx)−(1/(2y)) = ((q−x)/(qy)) (1/2)((dq/dx)−1) =1−(x/q) (dq/dx) −1 = 2−((2x)/q) ⇒(dq/dx) = 3−((2x)/q) (dq/dx) + ((2x)/q) = 3

$$\frac{{dy}}{{dx}}\:=\:\frac{{y}^{\mathrm{2}} +\mathrm{2}}{{y}\left({x}+\mathrm{2}+{y}^{\mathrm{2}} \right)} \\ $$$${set}\::\:{q}\:=\:{x}+\mathrm{2}+{y}^{\mathrm{2}} \:\Rightarrow\frac{{dq}}{{dx}}\:=\:\mathrm{1}+\mathrm{2}{y}\:\frac{{dy}}{{dx}} \\ $$$$\mathrm{2}{y}\:\frac{{dy}}{{dx}}\:=\:\frac{{dq}}{{dx}}−\mathrm{1}\Rightarrow\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}{y}}\:\frac{{dq}}{{dx}}−\frac{\mathrm{1}}{\mathrm{2}{y}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{2}{y}}\:\frac{{dq}}{{dx}}−\frac{\mathrm{1}}{\mathrm{2}{y}}\:=\:\frac{{q}−{x}}{{qy}}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{dq}}{{dx}}−\mathrm{1}\right)\:=\mathrm{1}−\frac{{x}}{{q}}\: \\ $$$$\frac{{dq}}{{dx}}\:−\mathrm{1}\:=\:\mathrm{2}−\frac{\mathrm{2}{x}}{{q}}\:\Rightarrow\frac{{dq}}{{dx}}\:=\:\mathrm{3}−\frac{\mathrm{2}{x}}{{q}} \\ $$$$\frac{{dq}}{{dx}}\:+\:\frac{\mathrm{2}{x}}{{q}}\:=\:\mathrm{3}\: \\ $$

Answered by bramlex last updated on 18/Jul/20

(∂M/∂y) = 2y ; (∂N/∂x) = −y ⇒non exact (∂N/∂x)−(∂M/∂y) = −3y is a function only in y . integrating factor u(y)=e^(∫(((−3y)/(y^2 +2))) dy) u(y)= e^(−(3/2)∫ ((d(y^2 +2))/(y^2 +2))) = (1/((y^2 +2)^(3/2) )) ⇒(((y^2 +2)/(√((y^2 +2)^3 )))) dx − (((xy+2y+y^3 )/(√((y^2 +2)^3 )))) dy=0 (1/(√(y^2 +2))) dx − ((x+2y+y^3 )/(√(y^2 +2))) dy=0 { (((∂f/∂x) = M(x,y)=(1/(√(y^2 +2))))),(((∂f/∂y)=N(x,y)=((x+2y+y^3 )/(√((y^2 +2)^3 ))))) :} F(x,y)=∫M(x,y)dx+g(y) g′(y) =((−y)/(√(y^2 +2))) g(y) = −(1/2)∫ ((d(y^2 +2))/((y^2 +2)^(1/2) )) g(y) = (√(y^2 +2)) F(x,y)= ∫ (dx/(√(y^2 +2))) + (√(y^2 +2)) F(x,y) = (x/(√(y^2 +2))) +(√(y^2 +2)) F(x,y) = ((x+y^2 +2)/(√(y^2 +2))) .★

$$\frac{\partial{M}}{\partial{y}}\:=\:\mathrm{2}{y}\:;\:\frac{\partial{N}}{\partial{x}}\:=\:−{y}\:\Rightarrow{non}\:{exact}\: \\ $$$$\frac{\partial{N}}{\partial{x}}−\frac{\partial{M}}{\partial{y}}\:=\:−\mathrm{3}{y}\:{is}\:{a}\:{function}\:{only}\:{in}\:{y}\:.\: \\ $$$${integrating}\:{factor}\:{u}\left({y}\right)={e}^{\int\left(\frac{−\mathrm{3}{y}}{{y}^{\mathrm{2}} +\mathrm{2}}\right)\:{dy}} \\ $$$${u}\left({y}\right)=\:{e}^{−\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{{d}\left({y}^{\mathrm{2}} +\mathrm{2}\right)}{{y}^{\mathrm{2}} +\mathrm{2}}} =\:\frac{\mathrm{1}}{\left({y}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\Rightarrow\left(\frac{{y}^{\mathrm{2}} +\mathrm{2}}{\sqrt{\left({y}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }}\right)\:{dx}\:−\:\left(\frac{{xy}+\mathrm{2}{y}+{y}^{\mathrm{3}} }{\sqrt{\left({y}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }}\right)\:{dy}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}}\:{dx}\:−\:\frac{{x}+\mathrm{2}{y}+{y}^{\mathrm{3}} }{\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}}\:{dy}=\mathrm{0} \\ $$$$\begin{cases}{\frac{\partial{f}}{\partial{x}}\:=\:{M}\left({x},{y}\right)=\frac{\mathrm{1}}{\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}}}\\{\frac{\partial{f}}{\partial{y}}={N}\left({x},{y}\right)=\frac{{x}+\mathrm{2}{y}+{y}^{\mathrm{3}} }{\sqrt{\left({y}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }}}\end{cases} \\ $$$${F}\left({x},{y}\right)=\int{M}\left({x},{y}\right){dx}+{g}\left({y}\right) \\ $$$${g}'\left({y}\right)\:=\frac{−{y}}{\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}} \\ $$$${g}\left({y}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left({y}^{\mathrm{2}} +\mathrm{2}\right)}{\left({y}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{1}/\mathrm{2}} }\: \\ $$$${g}\left({y}\right)\:=\:\sqrt{{y}^{\mathrm{2}} +\mathrm{2}} \\ $$$${F}\left({x},{y}\right)=\:\int\:\frac{{dx}}{\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}}\:+\:\sqrt{{y}^{\mathrm{2}} +\mathrm{2}} \\ $$$${F}\left({x},{y}\right)\:=\:\frac{{x}}{\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}}\:+\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}\: \\ $$$${F}\left({x},{y}\right)\:=\:\frac{{x}+{y}^{\mathrm{2}} +\mathrm{2}}{\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}}\:.\bigstar\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com