
Previous in Differential Equation Next in Differential Equation
Question Number 103958 by bemath last updated on 18/Jul/20
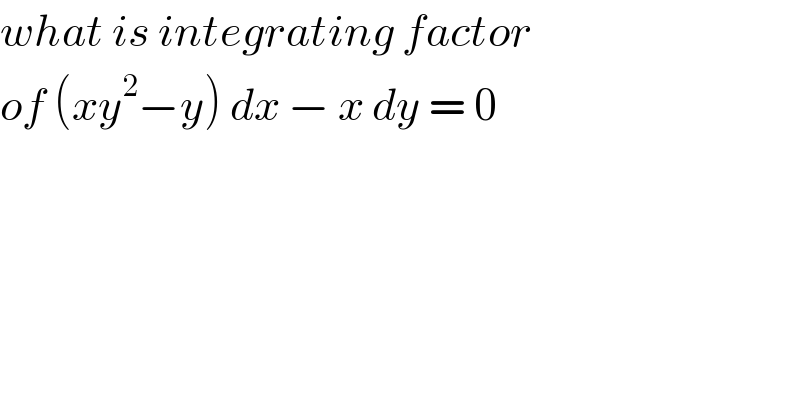
$${what}\:{is}\:{integrating}\:{factor} \\ $$$${of}\:\left({xy}^{\mathrm{2}} −{y}\right)\:{dx}\:−\:{x}\:{dy}\:=\:\mathrm{0} \\ $$
Answered by bramlex last updated on 18/Jul/20
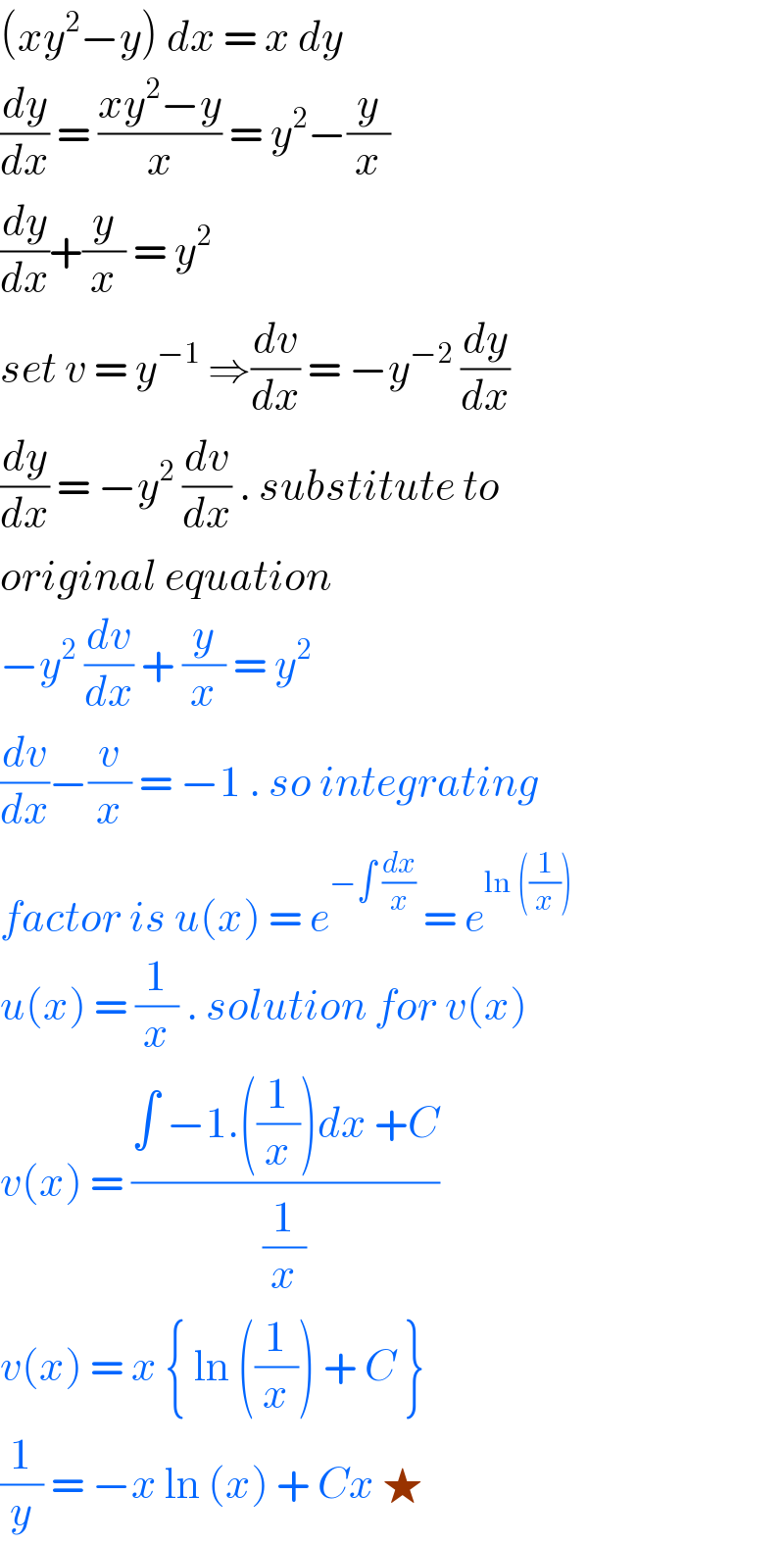
$$\left({xy}^{\mathrm{2}} −{y}\right)\:{dx}\:=\:{x}\:{dy}\: \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{xy}^{\mathrm{2}} −{y}}{{x}}\:=\:{y}^{\mathrm{2}} −\frac{{y}}{{x}} \\ $$$$\frac{{dy}}{{dx}}+\frac{{y}}{{x}}\:=\:{y}^{\mathrm{2}} \\ $$$${set}\:{v}\:=\:{y}^{−\mathrm{1}} \:\Rightarrow\frac{{dv}}{{dx}}\:=\:−{y}^{−\mathrm{2}} \:\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}\:=\:−{y}^{\mathrm{2}} \:\frac{{dv}}{{dx}}\:.\:{substitute}\:{to} \\ $$$${original}\:{equation}\: \\ $$$$−{y}^{\mathrm{2}} \:\frac{{dv}}{{dx}}\:+\:\frac{{y}}{{x}}\:=\:{y}^{\mathrm{2}} \\ $$$$\frac{{dv}}{{dx}}−\frac{{v}}{{x}}\:=\:−\mathrm{1}\:.\:{so}\:{integrating} \\ $$$${factor}\:{is}\:{u}\left({x}\right)\:=\:{e}^{−\int\:\frac{{dx}}{{x}}} \:=\:{e}^{\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}}\right)} \\ $$$${u}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}\:.\:{solution}\:{for}\:{v}\left({x}\right) \\ $$$${v}\left({x}\right)\:=\:\frac{\int\:−\mathrm{1}.\left(\frac{\mathrm{1}}{{x}}\right){dx}\:+{C}}{\frac{\mathrm{1}}{{x}}} \\ $$$${v}\left({x}\right)\:=\:{x}\:\left\{\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}}\right)\:+\:{C}\:\right\}\: \\ $$$$\frac{\mathrm{1}}{{y}}\:=\:−{x}\:\mathrm{ln}\:\left({x}\right)\:+\:{Cx}\:\bigstar\: \\ $$
