
Question Number 10397 by amir last updated on 07/Feb/17

Commented by mrW1 last updated on 07/Feb/17

$$\mathrm{I}\:\mathrm{think}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{maximum}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{premetre}\:\mathrm{of}\:\mathrm{the}\:\mathrm{trangle},\:\mathrm{but}\:\mathrm{a}\:\mathrm{minimum}. \\ $$$$ \\ $$$$\mathrm{Due}\:\mathrm{to}\:\mathrm{the}\:\mathrm{symmetry}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{seen} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{premetre}\:\mathrm{occurs} \\ $$$$\mathrm{when}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{line}\:\mathrm{tangents}\:\mathrm{the} \\ $$$$\mathrm{curve}\:\mathrm{at}\:\mathrm{point}\:\left(\mathrm{1},\:\mathrm{1}\right)\:\mathrm{or}\:\left(−\mathrm{1},−\mathrm{1}\right). \\ $$
Answered by mrW1 last updated on 07/Feb/17
![here the analytic solution: let B(t,s) a point on the curve xy=1. y=(1/x) s=(1/t) y′(x)=−(1/x^2 ) the slope of the tangent line at B is m_t =y′(t)=−(1/t^2 ) the equation of the tangent line is y−s=m_t (x−t) or y−(1/t)=−(1/t^2 )(x−t) the intersection points of tangent line with coordinate axes are C(0,c) and D(d,0). c−(1/t)=−(1/t^2 )(0−t) ⇒c=(2/t) 0−(1/t)=−(1/t^2 )(d−t) ⇒d=2t the premetre of triangle ΔOCD is P=OD+OC+CD=2t+(2/t)+(√((2t)^2 +((2/t))^2 )) =2[t+(1/t)+(√(t^2 +(1/t^2 )))]=2L L=t+(1/t)+(√(t^2 +(1/t^2 ))) (dL/dt)=1−(1/t^2 )+(1/(2(√(t^2 +(1/t^2 )))))×(2t−(2/t^3 )) =1−(1/t^2 )+(1/( (√(1+(1/t^4 )))))×(1−(1/t^4 )) =(1−(1/t^2 ))[1+((1+(1/t^2 ))/( (√(1+(1/t^4 )))))] (dP/dt)=0 ⇒ (dL/dt)=0 ⇒ 1−(1/t^2 )=0 ⇒t^2 =1 ⇒t=±1 i.e. the premetre P has minimum at (1,1) or (−1,−1) with t=1 we get: c=(2/t)=2 d=2t=2 P_(min) =2+2+(√(2^2 +2^2 ))=4+2(√2)](Q10403.png)
$${here}\:{the}\:{analytic}\:{solution}: \\ $$$$ \\ $$$${let}\:{B}\left({t},{s}\right)\:{a}\:{point}\:{on}\:{the}\:{curve}\:{xy}=\mathrm{1}. \\ $$$${y}=\frac{\mathrm{1}}{{x}} \\ $$$${s}=\frac{\mathrm{1}}{{t}} \\ $$$${y}'\left({x}\right)=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${the}\:{slope}\:{of}\:{the}\:{tangent}\:{line}\:{at}\:{B}\:{is} \\ $$$${m}_{{t}} ={y}'\left({t}\right)=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} } \\ $$$${the}\:{equation}\:{of}\:{the}\:{tangent}\:{line}\:{is} \\ $$$${y}−{s}={m}_{{t}} \left({x}−{t}\right)\:{or} \\ $$$${y}−\frac{\mathrm{1}}{{t}}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left({x}−{t}\right) \\ $$$${the}\:{intersection}\:{points}\:{of}\:{tangent} \\ $$$${line}\:{with}\:{coordinate}\:{axes}\:{are} \\ $$$${C}\left(\mathrm{0},{c}\right)\:{and}\:{D}\left({d},\mathrm{0}\right). \\ $$$${c}−\frac{\mathrm{1}}{{t}}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left(\mathrm{0}−{t}\right) \\ $$$$\Rightarrow{c}=\frac{\mathrm{2}}{{t}} \\ $$$$\mathrm{0}−\frac{\mathrm{1}}{{t}}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left({d}−{t}\right) \\ $$$$\Rightarrow{d}=\mathrm{2}{t} \\ $$$$ \\ $$$${the}\:{premetre}\:{of}\:{triangle}\:\Delta{OCD}\:{is} \\ $$$${P}={OD}+{OC}+{CD}=\mathrm{2}{t}+\frac{\mathrm{2}}{{t}}+\sqrt{\left(\mathrm{2}{t}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}}{{t}}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left[{t}+\frac{\mathrm{1}}{{t}}+\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\right]=\mathrm{2}{L} \\ $$$${L}={t}+\frac{\mathrm{1}}{{t}}+\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }} \\ $$$$\frac{{dL}}{{dt}}=\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}}×\left(\mathrm{2}{t}−\frac{\mathrm{2}}{{t}^{\mathrm{3}} }\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{4}} }}}×\left(\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{4}} }\right) \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\left[\mathrm{1}+\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{4}} }}}\right] \\ $$$$\frac{{dP}}{{dt}}=\mathrm{0} \\ $$$$\Rightarrow\:\frac{{dL}}{{dt}}=\mathrm{0}\:\Rightarrow\:\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{t}=\pm\mathrm{1} \\ $$$${i}.{e}.\:{the}\:{premetre}\:{P}\:{has}\:{minimum}\:{at} \\ $$$$\left(\mathrm{1},\mathrm{1}\right)\:{or}\:\left(−\mathrm{1},−\mathrm{1}\right) \\ $$$$ \\ $$$${with}\:{t}=\mathrm{1}\:{we}\:{get}: \\ $$$${c}=\frac{\mathrm{2}}{{t}}=\mathrm{2} \\ $$$${d}=\mathrm{2}{t}=\mathrm{2} \\ $$$${P}_{{min}} =\mathrm{2}+\mathrm{2}+\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$
Commented by amir last updated on 07/Feb/17
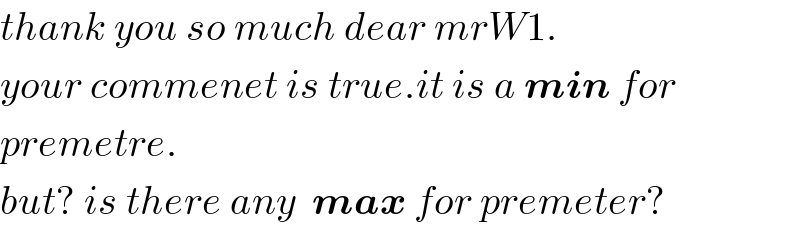
$${thank}\:{you}\:{so}\:{much}\:{dear}\:{mrW}\mathrm{1}. \\ $$$${your}\:{commenet}\:{is}\:{true}.{it}\:{is}\:{a}\:\boldsymbol{{min}}\:{for} \\ $$$${premetre}. \\ $$$${but}?\:{is}\:{there}\:{any}\:\:\boldsymbol{{max}}\:{for}\:{premeter}? \\ $$
Commented by mrW1 last updated on 07/Feb/17
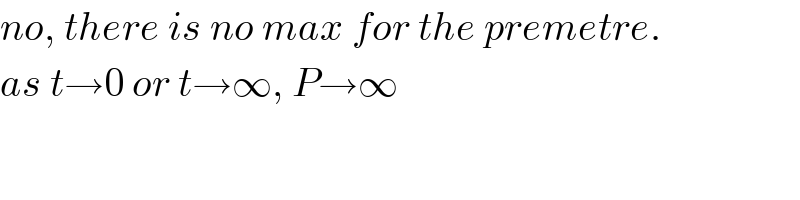
$${no},\:{there}\:{is}\:{no}\:{max}\:{for}\:{the}\:{premetre}. \\ $$$${as}\:{t}\rightarrow\mathrm{0}\:{or}\:{t}\rightarrow\infty,\:{P}\rightarrow\infty \\ $$
